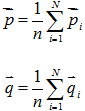迭代最近點演算法 Iterative Closest Points
【原文:http://www.cnblogs.com/GarfieldEr007/p/5116328.html】
研究生課程系列文章參見索引《在信科的那些課》
基本原理
假定已給兩個資料集P、Q, 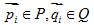 ,給出兩個點集的空間變換f使他們能進行空間匹配。這裡的問題是,f為一未知函式,而且兩點集中的點數不一定相同。解決這個問題使用的最多的方法是迭代最近點法(Iterative Closest Points Algorithm)。
,給出兩個點集的空間變換f使他們能進行空間匹配。這裡的問題是,f為一未知函式,而且兩點集中的點數不一定相同。解決這個問題使用的最多的方法是迭代最近點法(Iterative Closest Points Algorithm)。
基本思想是:根據某種幾何特性對資料進行匹配,並設這些匹配點為假想的對應點,然後根據這種對應關係求解運動引數。再利用這些運動引數對資料進行變換。並利用同一幾何特徵,確定新的對應關係,重複上述過程。
迭代最近點法目標函式
三維空間中兩個3D點,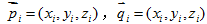 ,他們的歐式距離表示為:
,他們的歐式距離表示為:
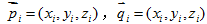 ,他們的歐式距離表示為:
,他們的歐式距離表示為: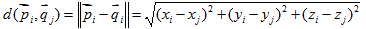
三維點雲匹配問題的目的是找到P和Q變化的矩陣R和T,對於 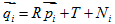 ,
,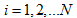 ,利用最小二乘法求解最優解使:
,利用最小二乘法求解最優解使:
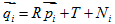 ,
,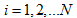 ,利用最小二乘法求解最優解使:
,利用最小二乘法求解最優解使: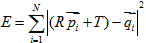
最小時的R和T。
資料預處理
實驗中採集了五個面的點如下所示:



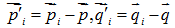
則上述最優化目標函式可以轉化為:
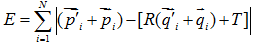
最優化問題分解為:
- 求使E最小的
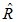
- 求使
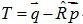
- //計算點雲P的中心點mean
- void CalculateMeanPoint3D(vector<Point3D> &P, Point3D &mean)
- {
- vector<Point3D>::iterator it;
- mean.x = 0;
- mean.y = 0;
- mean.z = 0;
- for(it=P.begin(); it!=P.end(); it++){
- mean.x += it->x;
- mean.y += it->y;
- mean.z += it->z;
- }
- mean.x = mean.x/P.size();
- mean.y = mean.y/P.size();
- mean.z = mean.z/P.size();
- }

利用控制點求初始旋轉矩陣
在確定對應關係時,所使用的幾何特徵是空間中位置最近的點。這裡,我們甚至不需要兩個點集中的所有點。可以指用從某一點集中選取一部分點,一般稱這些點為控制點(Control Points)。這時,配準問題轉化為: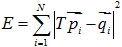
在Geomagic Studio中利用三個點就可以進行兩個模型的“手動註冊”(感覺這裡翻譯的不好,Registration,應該為“手動匹配”)。

我們將手動選擇的三個點匯出,作為實驗初始的控制點:

對於第i對點,計算點對的矩陣 Ai:
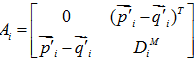
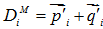 ,
,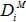 為
為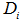 的轉置矩陣。
的轉置矩陣。
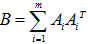
原最優化問題可以轉為求B的最小特徵值和特徵向量,具體程式碼:
一次旋轉計算得到的矩陣如下:

效果在Geomagic Studio中顯示如圖:

具體為對點集P中每個點,找Q中離他最近的點作為對應點。在某一步利用前一步得到的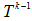 ,求使下述函式最小的
,求使下述函式最小的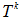 :
:
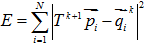 這裡,
這裡, 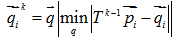
迴圈結束後能得到較好的匹配效果:


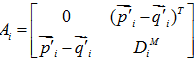
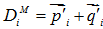 ,
,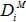 為
為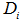 的轉置矩陣。
的轉置矩陣。(*這裡在査老師的課上給了一個錯誤的矩陣變換公式)
對於每一對矩陣Ai,計算矩陣B: 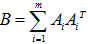
- double B[16];
- for(int i=0;i<16;i++)
- B[i]=0;
- for(itp=P.begin(),itq=Q.begin();itp!=P.end();itp++,itq++ ){
- double divpq[3]={itp->x,itp->y,itp->z};
- double addpq[3]={itp->x,itp->y,itp->z};
- double q[3]={itq->x,itq->y,itq->z};
- MatrixDiv(divpq,q,3,1);
- MatrixAdd(addpq,q,3,1);
- double A[16];
- for(int i=0;i<16;i++)
- A[i]=0;
- for(int i=0;i<3;i++){
- A[i+1]=divpq[i];
- A[i*4+4]=divpq[i];
- A[i+13]=addpq[i];
- }
- double AT[16],AMul[16];
- MatrixTran(A,AT,4,4);
- MatrixMul(A,AT,AMul,4,4,4,4);
- MatrixAdd(B,AMul,4,4);
- }
原最優化問題可以轉為求B的最小特徵值和特徵向量,具體程式碼:
- //使用奇異值分解計算B的特徵值和特徵向量
- double eigen, qr[4];
- MatrixEigen(B, &eigen, qr, 4);
- //計算n階正定陣m的特徵值分解:eigen為特徵值,q為特徵向量
- void MatrixEigen(double *m, double *eigen, double *q, int n)
- {
- double *vec, *eig;
- vec = new double[n*n];
- eig = new double[n];
- CvMat _m = cvMat(n, n, CV_64F, m);
- CvMat _vec = cvMat(n, n, CV_64F, vec);
- CvMat _eig = cvMat(n, 1, CV_64F, eig);
- //使用OpenCV開源庫中的矩陣操作求解矩陣特徵值和特徵向量
- cvEigenVV(&_m, &_vec, &_eig);
- *eigen = eig[0];
- for(int i=0; i<n; i++)
- q[i] = vec[i];
- delete[] vec;
- delete[] eig;
- }
- //計算旋轉矩陣
- void CalculateRotation(double *q, double *R)
- {
- R[0] = q[0]*q[0] + q[1]*q[1] - q[2]*q[2] - q[3]*q[3];
- R[1] = 2.0 * (q[1]*q[2] - q[0]*q[3]);
- R[2] = 2.0 * (q[1]*q[3] + q[0]*q[2]);
- R[3] = 2.0 * (q[1]*q[2] + q[0]*q[3]);
- R[4] = q[0]*q[0] - q[1]*q[1] + q[2]*q[2] - q[3]*q[3];
- R[5] = 2.0 * (q[2]*q[3] - q[0]*q[1]);
- R[6] = 2.0 * (q[1]*q[3] - q[0]*q[2]);
- R[7] = 2.0 * (q[2]*q[3] + q[0]*q[1]);
- R[8] = q[0]*q[0] - q[1]*q[1] - q[2]*q[2] + q[3]*q[3];
- }
平移矩陣計算
2.4中可以得到選擇矩陣的4元數表示,由於在"平行移動和旋轉的分離"中,我們將最優問題分解為:- 求使E最小的
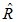
- 求使
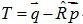
- //通過特徵向量計算旋轉矩陣R1和平移矩陣T1
- CalculateRotation(qr, R1);
- double mean_Q[3]={_mean_Q.x,_mean_Q.y,_mean_Q.z};
- double mean_P[3]={_mean_P.x,_mean_P.y,_mean_P.z};
- double meanT[3]={0,0,0};
- int nt=0;
- for(itp=P.begin(),itq=Q.begin();itp!=P.end();itp++,itq++ ){
- double tmpP[3]={itp->x,itp->y,itp->z};
- double tmpQ[3]={itq->x,itq->y,itq->z};
- double tmpMul[3];
- MatrixMul(R1, mean_P, tmpMul, 3, 3, 3, 1);
- MatrixDiv(tmpQ,tmpMul,3,1);
- MatrixAdd(meanT,tmpQ,3,1);
- nt++;
- }
- for(int i=0; i<3; i++)
- T1[i] = meanT[i]/(double)(nt);
一次旋轉計算得到的矩陣如下:

效果在Geomagic Studio中顯示如圖:

迭代最近點
在初始匹配之後,所點集P`中所有點做平移變化,在比較點集合P`和Q`的匹配度,(或迭代次數)作為演算法終止的條件。具體為對點集P中每個點,找Q中離他最近的點作為對應點。在某一步利用前一步得到的
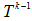 ,求使下述函式最小的
,求使下述函式最小的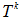 :
: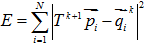
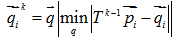
- //計算誤差和d
- d = 0.0;
- if(round==1){
- FindClosestPointSet(data,P,Q);
- }
- int pcount=0;
- for(itp = P.begin(),itq=Q.begin();itp!=P.end(); itp++, itq++){
- double sum = (itp->x - itq->x)*(itp->x - itq->x) + (itp->y - itq->y)*(itp->y - itq->y)
- + (itp->z - itq->z)*(itp->z - itq->z);
- d += sum;
- pcount++;
- }
- d=d/(double)(pcount);
迴圈結束後能得到較好的匹配效果:

封裝後的效果圖:

相關文章
- [LeetCode] 3Sum Closest 最近三數之和LeetCode
- 演算法3Sum Closest演算法
- 【演算法】轉載:Iterative vs. Recursive Approaches演算法APP
- 973. K Closest Points to Origin(Leetcode每日一題-2020.11.09)LeetCode每日一題
- jQuery closest()jQuery
- Grid Points
- KDTree求平面最近點對
- 迭代閾值分割演算法演算法
- Important Points for Inheritance in JavaImportJava
- 開源點雲庫torch-points3d的嘗試S33D
- Point Cloud Library學習之ICP迭代最近點匹配法NDT2D正態分佈轉換法Cloud
- 不動點迭代(Fixed Point Iteration)
- Git 中的演算法-最近公共祖先Git演算法
- 最近關於工作的幾點思考
- 計算幾何——平面最近點對
- Machine Learning - Basic pointsMac
- Objects as Points 論文總結Object
- Restore Points 制定回退方案REST
- 4.2.2、容器,演算法,迭代器 初識演算法
- Leetcode 3Sum ClosestLeetCode
- LintCode-Subarray Sum Closest
- Leetcode-3Sum ClosestLeetCode
- 論文解讀(IGSD)《Iterative Graph Self-Distillation》
- 高階搜尋演算法之迭代加深演算法
- 平面最近點對 & 最小周長三角形 & 曼哈頓距離最近
- 最近學習了限流相關的演算法演算法
- C++實現蠻力最近對演算法C++演算法
- LCA最近公共祖先 線上演算法和離線演算法 模板演算法
- Leetcode 16 3Sum ClosestLeetCode
- 3Sum Closest leetcode javaLeetCodeJava
- JavaScript專項演算法題(7):Iterators迭代器JavaScript演算法
- Leetcode Max Points on a LineLeetCode
- Points on Cycle (hdu1700,幾何)
- CF 295E Yaroslav and Points(Splay)ROS
- Game with points(數學,難度中)GAM
- 演算法學習筆記(5): 最近公共祖先(LCA)演算法筆記
- 如何計算二叉樹中葉節點的數量 - Java迭代和遞迴演算法二叉樹Java遞迴演算法
- [LeetCode] 681. Next Closest TimeLeetCode