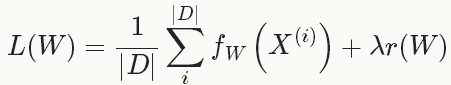Caffe中的優化方法

查志強發表於2015-08-06
優化

【原文：http://demo.netfoucs.com/danieljianfeng/article/details/42931721】

在Deep Learning中，往往loss function是非凸的，沒有解析解，我們需要通過優化方法來求解。Caffe通過協調的進行整個網路的前向傳播推倒以及後向梯度對引數進行更新，試圖減小損失。

 Caffe已經封裝好了三種優化方法，分別是Stochastic Gradient Descent (SGD), AdaptiveGradient (ADAGRAD), and Nesterov’s Accelerated Gradient (NAG)。


 Solver的流程：

1.     設計好需要優化的物件，以及用於學習的訓練網路和用於評估的測試網路。

2.     通過forward和backward迭代的進行優化來跟新引數

3.     定期的評價測試網路

4.     在優化過程中顯示模型和solver的狀態

 每一步迭代的過程

1.     通過forward計算網路的輸出和loss

2.     通過backward計算網路的梯度

3.     根據solver方法，利用梯度來對引數進行更新

4.     根據learning rate，history和method來更新solver的狀態

 

和Caffe模型一樣，Caffe solvers也可以CPU / GPU執行。


1. Methods

Solver方法一般用來解決loss函式的最小化問題。對於一個資料集D，需要優化的目標函式是整個資料集中所有資料loss的平均值。


其中， r(W)是正則項，為了減弱過擬合現象。

如果採用這種Loss 函式，迭代一次需要計算整個資料集，在資料集非常大的這情況下，這種方法的效率很低，這個也是我們熟知的梯度下降採用的方法。


在實際中，會採用整個資料集的一個mini-batch，其數量為N<<|D|，此時的loss 函式為：
 


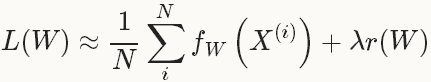
有了loss函式後，就可以迭代的求解loss和梯度來優化這個問題。在神經網路中，用forward pass來求解loss，用backward pass來求解梯度。


1.1 SGD

型別：SGD
隨機梯度下降（Stochastic gradient descent）通過negative梯度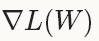和上一次的權重更新值V_t的線性組合來更新W，迭代公式如下：


 
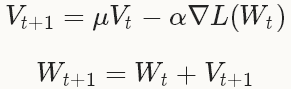
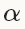
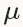
其中，learning rate  是negative梯度的權重，momentum是上一次更行的權重。這兩個引數需要通過tuning來得到最好的結果，一般是根據經驗設定的。如果你不知道如何設定這些引數，可以參考下面的經驗法則，如果需要了解更多的引數設定技巧可以參考論文Stochastic Gradient Descent Tricks [1]。


設定learningrate和momentum的經驗法則

例子

<span style="background-color: rgb(255, 255, 255);">base_lr: 0.01     # begin training at a learning rate of0.01 = 1e-2 lr_policy: "step" # learning ratepolicy: drop the learning rate in "steps"                  # by a factor of gamma everystepsize iterations gamma: 0.1        # drop the learning rate by a factor of10                  # (i.e., multiply it by afactor of gamma = 0.1) stepsize: 100000  # drop the learning rate every 100K iterations max_iter: 350000  # train for 350K iterations total momentum: 0.9</span>

在深度學習中使用SGD，好的初始化引數的策略是把learning rate設為0.01左右，在訓練的過程中，如果loss開始出現穩定水平時，對learning rate乘以一個常數因子（比如，10），這樣的過程重複多次。此外，對於momentum，一般設為0.9，momentum可以讓使用SGD的深度學習方法更加穩定以及快速，這次初始引數參論文ImageNet Classification with Deep Convolutional Neural Networks [2]。

上面的例子中，初始化learning rate的值為0.01，前100K迭代之後，更新learning rate的值（乘以gamma）得到0.01*0.1=0.001，用於100K-200K的迭代，一次類推，直到達到最大迭代次數350K。

Note that the momentum setting μ effectively multiplies the size of your updates by a factor of 11−μ after many iterations of training, so if you increase μ, it may be a good idea to decrease α accordingly (and vice versa).

For example, with μ=0.9, we have an effective update size multiplier of 11−0.9=10. If we increased the momentum to μ=0.99, we’ve increased our update size multiplier to 100, so we should drop α (base_lr) by a factor of 10.

上面的設定只能作為一種指導，它們不能保證在任何情況下都能得到最佳的結果，有時候這種方法甚至不work。如果學習的時候出現diverge（比如，你一開始就發現非常大或者NaN或者inf的loss值或者輸出），此時你需要降低base_lr的值（比如，0.001），然後重新訓練，這樣的過程重複幾次直到你找到可以work的base_lr。


1.2 AdaGrad

型別：ADAGRAD

自適應梯度（adaptive gradient）[3]是基於梯度的優化方法（like SGD），以作者的話說就是，“find needles in haystacks in the form of very predictive but rarely seen features”。給定之前所有迭代的更新資訊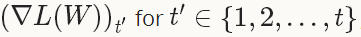，每一個W的第i個成分的更新如下：


 
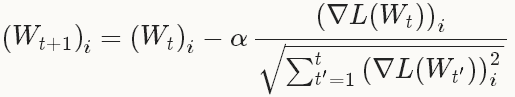
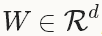
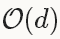
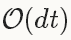
在實踐中需要注意的是，權重，AdaGrad的實現（包括在Caffe中）只需要使用額外的儲存來儲存歷史的梯度資訊，而不是的儲存（這個需要獨立儲存每一個歷史梯度資訊）。（自己沒有理解這邊的意思）


1.3 NAG

型別：NAG
Nesterov 的加速梯度法（Nesterov’s accelerated gradient）作為凸優化中最理想的方法，其收斂速度可以達到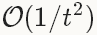而不是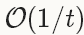。但由於深度學習中的優化問題往往是非平滑的以及非凸的（non-smoothness and non-convexity），在實踐中NAG對於某類深度學習的結構可以成為非常有效的優化方法，比如deep MNIST autoencoders[5]。


權重的更新和SGD的的非常類似：


 
不同的是在計算梯度的時候，在NAG中求解權重加上momentum的梯度，而在SGD中只是簡單的計算當前權重的梯度。


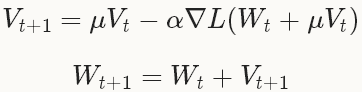
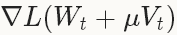
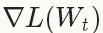
2. 參考：

[1] L. Bottou. Stochastic Gradient Descent Tricks. Neural Networks: Tricks of the Trade: Springer, 2012.
[2] A. Krizhevsky, I. Sutskever, and G. Hinton. ImageNet Classification with Deep Convolutional Neural Networks. Advances in Neural Information Processing Systems, 2012.
[3] J. Duchi, E. Hazan, and Y. Singer. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. The Journal of Machine Learning Research, 2011.
[4] Y. Nesterov. A Method of Solving a Convex Programming Problem with Convergence Rate O(1/k√). Soviet Mathematics Doklady, 1983.
[5] I. Sutskever, J. Martens, G. Dahl, and G. Hinton. On the Importance of Initialization and Momentum in Deep Learning. Proceedings of the 30th International Conference on Machine Learning, 2013.
[6] http://caffe.berkeleyvision.org/tutorial/solver.html

相關文章