第四章 使用OpenCV探測來至運動的結構——Chapter 4:Exploring Structure from Motion Using OpenCV
【原文:http://www.csdn123.com/html/mycsdn20140110/57/57fc0284cb8b01ad9d9565f8a8bf7ec9.html】
僅供參考,還未執行程式,理解部分有誤,請參考英文原版。
綠色部分非文章內容,是個人理解。
轉載請註明:http://blog.csdn.net/raby_gyl/article/details/17471617
Chapter 4:Exploring Structure from Motion Using OpenCV
在這一章,我們將討論來至運動結構(Structure from Motion,SfM)的概念,或者從一個運動的相機拍攝到的影象中更好的推測提取出來的幾何結構,使用OpenCV的API函式可以幫助我們完成這個任務。首先,讓我們將我們使用的冗長的方法約束為使用單個攝像機,通常稱為單目方法,並且是一組分離的和稀疏的視訊幀而不是連續的視訊流。這兩個約束在很大程度上簡化了系統,這個系統我們將在接下來的頁碼中進行描述,並且幫助我們理解任何SfM方法的原理。為了實現我們的方法,我們將跟隨Hartley和Zisserman的腳步(後面稱作H和Z),伴隨著他們有創意的書——《計算機視覺中的多視覺幾何》的第9章到第12章的記錄。
在這一章,我們將涉及到以下內容:
1、來至運動結構的概念
2、從一對影象中估計攝像機的運動
3、重構場景
4、從多個檢視中重構
5、重構提純(Refinement of the reconstruction)
6、視覺化3D點雲
本章自始自終假定使用一個標定過的相機——預先標定的相機。在計算機視覺中標定是一個普遍存在的操作,在OpenCV中得到了很好的支援,我們可以使用在前一章討論的命令列工具來完成標定。因此,我們假定攝像機內引數存在,並且具體化到K矩陣中,K矩陣為攝像機標定過程的一個結果輸出。
為了在語言方面表達的清晰,從現在開始我們將單個攝像機稱為場景的單個檢視而不是光學和獲取影象的硬體。一個攝像機在空間中有一個位置,一個觀察的方向。在兩個攝像機中,有一個平移成分(空間運動)和一個觀察方向的旋轉。我們同樣對場景中的點統一一下術語,世界(world),現實(real),或者3D,意思是一樣的,即我們真實世界存在的一個點。這同樣適用於影象中的點或者2D,這些點在影象座標系中,是在這個位置和時間上一些現實的3D點投影到攝像機感測器上形成的。
在這一章的程式碼部分,你將注意參考《計算視覺中的多視覺幾何》(Multiple View Geometry in Computer Vision),例如,//HZ9.12,這指的是這本書的第9章第12個等式。同樣的,文字僅包括程式碼的摘錄,而完整的程式碼包含在伴隨著這本書的材料中。
來至運動結構的概念——Structure from Motion concepts
第一個我們應當區別的是立體(Stereo or indeed any multiview),使用標準平臺的三維重建和SfM之間的差異。在兩個或多個攝像機的平臺中,假定我們已經知道了兩個攝像機之間的運動,而在SfM中,我們實際上不知道這個運動並且我們希望找到它。標準平臺,來至觀察的一個過分簡單的點,可以得到一個更加精確的3D幾何的重構,因為在估計多個攝像機間距離和旋轉時沒有誤差(距離和旋轉已知)。實現一個SfM系統的第一步是找到相機之間的運動。OpenCV可以幫助我們在許多方式上獲得這個運動,特別地,使用findFundamentalMat函式。
讓我們想一下選擇一個SfM演算法背後的目的。在很多情況下,我們希望獲得場景的幾何。例如,目標相對於相機的位置和他們的形狀是什麼。假定我們知道了捕獲同一場景的攝像機之間的運動,從觀察的一個合理的相似點,現在我們想重構這個幾何。在計算視覺術語中稱為三角測量(triangulation),並且有很多方法可以做這件事。它可以通過 射線相交的方法完成,這裡我們構造兩個射線:來至於每個攝像機投影中心的點和每一個影象平面上的點。理想上,這兩個射線在空間中將相交於真實世界的一個3D點(這個3D點在每個攝像機中成像),如下面圖表展示:
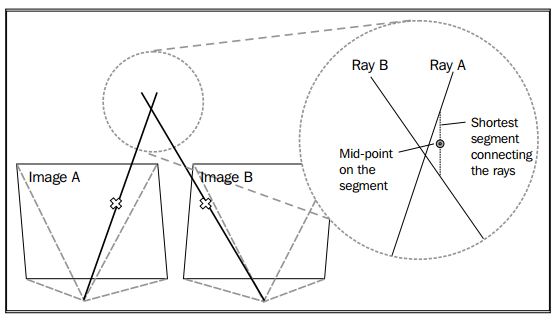
實際上,射線相交非常不可靠。H和Z推薦不使用它。這是因為兩個射線通常不能相交,讓我們回到使用連線兩個射線的最短線段上的中間點。相反,H和Z建議一些方法來三角化3D點(trianglulate 3D points,三角化3D點就是計算3D點的座標,可以通過後面的內容加以理解),這些方法中我們將在重構場景部分討論兩個。OpenCV現在的版本沒有包含三角測量(triangulation)的API,因此,這部分我們將自己編寫程式碼。
學習完如何從兩個檢視恢復3D幾何之後,我們將看到我們是怎麼樣加入更多的同一個場景的檢視來獲得更豐富的重構。在那時,大部分的SfM方法試圖依靠束調整(Bundle Adjustment)來優化我們的攝像機和3D點一束估計位置(the bundle of estimated positon),這部分內容在重構提純部分(Refinement of the reconstruction section)。OpenCV在新的影象拼接的工具箱內包含了用來束調整的方法。然而,使OpenCV和C++完美結合的工作是豐富的外部工具,這些工具可以很容易地整合到一起。因此,我們將看到如何如何整合一個外部的束調節器——靈巧的SSBA庫。
既然我們已經描述了使用OpenCV實現我們的SfM方法的一個概括,我們將看到每個分成是如何實現的。
從一對影象中估計攝像機的運動——Estimating the camera motion from a pair of images
事實上,在我們開始著手兩個攝像機之間的運動之前,讓我們檢查一下我們手邊用來執行這個操作的輸入和工具。首先,我們有來至(希望並不是非常)不同空間位置的同一場景的兩個影象。這是一個強大的資產,並且我們將確保使用它。現在工具都有了,我們應當看一下數學物件,來對我們的影象,相機和場景施加約束。
兩個非常有用的數學物件是基礎矩陣(用F表示)和本徵矩陣(用E表示)。除了本徵矩陣是假設使用的標定的相機,它們非常相似。這種情況針對我們,所以我們將選著它。OpenCV函式僅允許我們通過findFundamentalMat函式找到基礎矩陣。然而,我們非常簡單地使用標定矩陣(calibration matrix)K從本徵矩陣中獲得基礎矩陣,如下:
Mat_<double> E = K.t() * F * K; //according to HZ (9.12)本徵矩陣,是一個3×3大小的矩陣,使用x’Ex=0在影象中的一點和另外一個影象中的一點之間施加了一個約束,這裡x是影象一中的的一點,x’是影象二中與之相對應的一點。這非常有用,因為我們將要看到。我們使用的另一個重要的事實是本徵矩陣是我們用來為我們的影象恢復兩個相機的所有需要,儘管只有尺度,但是我們以後會得到。因此,如果我們獲得了本徵矩陣,我們知道每一個相機在空間中的位置,並且知道它們的觀察方向,如果我們有足夠這樣的約束等式,那麼我們可以簡單地計算出這個矩陣。簡單的因為每一個等式可以用來解決矩陣的一小部分。事實上,OpenCV允許我們僅使用7個點對來計算它,但是我們希望獲得更多的點對來得到一個魯棒性的解。
使用豐富的特徵描述子進行點匹配——Point matching using rich feature descriptors
現在我們將使用我們的約束等式來計算本徵矩陣。為了獲得我們的約束,記住對於影象A中的每一個點我們必須在影象B中找到一個與之相對應的點。我們怎樣完成這個匹配呢?簡單地通過使用OpenCV的廣泛的特徵匹配框架,這個框架在過去的幾年了已經非常成熟。
在計算機視覺中,特徵提取和描述子匹配是一個基礎的過程,並且用在許多方法中來執行各種各樣的操作。例如,檢測影象中一個目標的位置和方向,或者通過給出一個查詢影象在大資料影象中找到相似的影象。從本質上講,提取意味著在影象中選擇點,使得獲得好的特徵,並且為它們計算一個描述子。一個描述子是含有多個資料的向量,用來描述在一個影象中圍繞著特徵點的周圍環境。不同的方法有不同的長度和資料型別來表示描述子向量。匹配是使用它的描述子從另外一個影象中找到一組與之對應的特徵。OpenCV提供了非常簡單和有效的方法支援特徵提取和匹配。關於特徵匹配的更多資訊可以在Chapter 3少量(無)標記擴增實境中找到。
讓我們檢查一個非常簡單特徵提取和匹配方案:
// detectingkeypoints
SurfFeatureDetectordetector();
vector<KeyPoint> keypoints1, keypoints2;
detector.detect(img1, keypoints1);
detector.detect(img2, keypoints2);
// computing descriptors
SurfDescriptorExtractor extractor;
Mat descriptors1, descriptors2;
extractor.compute(img1, keypoints1, descriptors1);
extractor.compute(img2, keypoints2, descriptors2);
// matching descriptors
BruteForceMatcher<L2<float>> matcher;
vector<DMatch> matches;
matcher.match(descriptors1, descriptors2, matches);你可能已經看到類似的OpenCV程式碼,但是讓我們快速的回顧一下它。我們的目的是獲得三個元素:兩個影象的特徵點,特徵點的描述子,和兩個特徵集的匹配。OpenCV提供了一組特徵檢測器、描述子提取器和匹配器。在這個簡單例子中,我們使用SurfFeatureDetector函式來獲得SURF(Speeded-Up-Robust Features)特徵的2D位置,並且使用SurfDescriptorExtractor函式來獲得SURF描述子。我們使用一個brute-force匹配器來獲得匹配,這是一個最直接方式來匹配兩個特徵集,該方法是通過比較第一個集中的每一個特徵和第一個集的每一個特徵並且獲得最好的匹配來實現的。
在下一個影象中,我們將看到兩個影象上的特徵點的匹配:(這兩個影象來至於the Fountain-P11 sequence,可以在網址中找到:http://cvlab.epfl.ch/~strecha/multiview/denseMVS.html.)

實際上,像我們執行的原始匹配(raw matching),只有到達某一程度時執行效果才比較好並且許多匹配可能是錯誤的。因此,大多數SfM方法對原始匹配進行一些濾波方式來確保正確和減少錯誤。一種濾波方式叫做交叉檢驗濾波,它內建於OpenCV的brute-force匹配器中。也就是說,如果第一個影象的一個特徵匹配第二個影象的一個特徵,並且通過反向檢查,第二個影象的特徵也和第一個影象的特徵匹配,那麼這個匹配被認為是正確的。另一個常見的濾波機制(該機制用在提供的程式碼中)是基於同一場景的兩個影象並且在他們之間存在某一種立體視覺關係,這樣的一個事實基礎之上來濾波的。在實踐中,這個濾波器嘗試採用魯棒性的演算法來計算這個基礎矩陣,我們將會在尋找相機矩陣(Finding camera matrices)部分學習這種計算方法,並且保留由該計算得到的帶有小誤差的特徵對。
使用光流進行點匹配——Point matching using optical flow
一個替代使用豐富特徵(如SURF)匹配的方法,是使用optical flow(OF光流)進行匹配。下面的資訊框提供了光流的一個簡短的概述。最近的OpenCV為從兩個影象獲得流場擴充套件了API,並且現在更快,更強大。我們將嘗試使用它作為匹配特徵的一個替代品。
【註釋:
光流是匹配來至一幅影象選擇的點到另外一幅影象選著點的過程,假定這兩個影象是一個視訊序列的一部分並且它們彼此非常相近。大多數的光流方法比較一個小的區域,稱為搜尋視窗或者塊,這些塊圍繞著影象A中的每一點和同樣區域的影象B中的每一點。遵循計算機視覺中一個非常普通的規則,稱為亮度恆定約束(brightness constancy constraint)(和其他名字),影象中的這些小塊從一個影象到另外一個影象不會有太大的變化,因此,他們的幅值差接近於0。除了匹配塊,更新的光流方法使用一些額外的方法來獲得更好的結果。其中一個方法就是使用影象金字塔,它是影象越來越小的尺寸(大小)版本,這考慮到了工作的從粗糙到精緻——計算機視覺中一個非常有用的技巧。另外一個方法是定義一個流場上的全域性約束,假定這些點相互靠近,向同一方向一起運動。在OpenCV中,一個更加深入的光流方法可以在Chapter Developing Fluid Wall Using the Microsoft Kinect中找到,這個書可以在出版社網站上訪問到。】
在OpenCV中,使用光流相當的簡單,可以通過呼叫calcOpticalFlowPyrLK函式來實現。我們想要儲存光流的結果匹配,像使用豐富的特徵那樣,在未來,我們希望兩種方法可以互換。為了這個目標,我們必須安裝一個特殊的匹配方法——可以與基於特徵的方法互換,這將在下面的程式碼中看到:
Vector<KeyPoint>left_keypoints,right_keypoints;
// Detect keypoints in the left and right images
FastFeatureDetectorffd;
ffd.detect(img1, left_keypoints);
ffd.detect(img2, right_keypoints);
vector<Point2f>left_points;
KeyPointsToPoints(left_keypoints,left_points);
vector<Point2f>right_points(left_points.size());
// making sure images are grayscale
Mat prevgray,gray;
if (img1.channels() == 3) {
cvtColor(img1,prevgray,CV_RGB2GRAY);
cvtColor(img2,gray,CV_RGB2GRAY);
} else {
prevgray = img1;
gray = img2;
}
// Calculate the optical flow field:
// how each left_point moved across the 2 images
vector<uchar>vstatus; vector<float>verror;
calcOpticalFlowPyrLK(prevgray, gray, left_points, right_points,
vstatus, verror);
// First, filter out the points with high error
vector<Point2f>right_points_to_find;
vector<int>right_points_to_find_back_index;
for (unsigned inti=0; i<vstatus.size(); i++) {
if (vstatus[i] &&verror[i] < 12.0) {
// Keep the original index of the point in the
// optical flow array, for future use
right_points_to_find_back_index.push_back(i);
// Keep the feature point itself
right_points_to_find.push_back(j_pts[i]);
} else {
vstatus[i] = 0; // a bad flow
}
}
// for each right_point see which detected feature it belongs to
Mat right_points_to_find_flat = Mat(right_points_to_find).
reshape(1,to_find.size()); //flatten array
vector<Point2f>right_features; // detected features
KeyPointsToPoints(right_keypoints,right_features);
Mat right_features_flat = Mat(right_features).reshape(1,right_
features.size());
// Look around each OF point in the right image
// for any features that were detected in its area
// and make a match.
BFMatchermatcher(CV_L2);
vector<vector<DMatch>>nearest_neighbors;
matcher.radiusMatch(
right_points_to_find_flat,
right_features_flat,
nearest_neighbors,
2.0f);
// Check that the found neighbors are unique (throw away neighbors
// that are too close together, as they may be confusing)
std::set<int>found_in_right_points; // for duplicate prevention
for(inti=0;i<nearest_neighbors.size();i++) {
DMatch _m;
if(nearest_neighbors[i].size()==1) {
_m = nearest_neighbors[i][0]; // only one neighbor
} else if(nearest_neighbors[i].size()>1) {
// 2 neighbors – check how close they are
double ratio = nearest_neighbors[i][0].distance /
nearest_neighbors[i][1].distance;
if(ratio < 0.7) { // not too close
// take the closest (first) one
_m = nearest_neighbors[i][0];
} else { // too close – we cannot tell which is better
continue; // did not pass ratio test – throw away
}
} else {
continue; // no neighbors... :(
}
// prevent duplicates
if (found_in_right_points.find(_m.trainIdx) == found_in_right_points.
end()) {
// The found neighbor was not yet used:
// We should match it with the original indexing
// ofthe left point
_m.queryIdx = right_points_to_find_back_index[_m.queryIdx];
matches->push_back(_m); // add this match
found_in_right_points.insert(_m.trainIdx);
}
}
cout<<"pruned "<< matches->size() <<" / "<<nearest_neighbors.size()
<<" matches"<<endl;函式KeyPointsToPoints和PointsToKeyPoints是用來進行cv::Point2f和cv::KeyPoint結構體之間相互轉換的簡單方便的函式。從先前的程式碼片段我們可以看到一些有趣的事情。第一個注意的事情是,當我們使用光流時,我們的結果表明,一個特徵從左手邊影象的一個位置移動到右手邊影象的另外一個位置。但是我們有一組在右手邊影象中檢測到的新的特徵,在光流中從這個影象到左手邊影象的特徵不一定是對齊的。我們必須使它們對齊。為了找到這些丟失的特徵,我們使用一個k鄰近(KNN)半徑搜尋,這給出了我們兩個特徵,即感興趣的點落入了2個畫素半徑範圍內。
我們可以看得到另外一個事情是用來測試KNN的比例的實現,在SfM中這是一種常見的減少錯誤的方法。實質上,當我們對左手邊影象上的一個特徵和右手邊影象上的一個特徵進行匹配時,它作為一個濾波器,用來移除混淆的匹配。如果右手邊影象中兩個特徵太靠近,或者它們之間這個比例(the rate)太大(接近於1.0),我們認為它們混淆了並且不使用它們。我們也安裝一個雙重防禦濾波器來進一步修剪匹配。
下面的影象顯示了從一幅影象到另外一幅影象的流場。左手邊影象中的分紅色箭頭表示了塊從左手邊影象到右手邊影象的運動。在左邊的第二個影象中,我們看到一個放大了的小的流場區域。粉紅色箭頭再一次表明了塊的運動,並且我們可以通過右手邊的兩個原影象的片段看到它的意義。在左手邊影象上可視的特徵正在向左移動穿過影象,粉紅色箭頭的方向在下面的影象中展示:

使用光流法代替豐富特徵的優點是這個過程通常更快並且可以適應更多的點,使重構更加稠密。在許多光流方法中也有一個塊整體運動的統一模型,在這個模型中,豐富的特徵匹配通常不考慮。使用光流要注意的是對於從同一個硬體獲取的連續影象,它處理的很快,然而豐富的特徵通常不可知。它們之間的差異源於這樣的一個事實:光流法通常使用非常基礎的特徵,像圍繞著一個關鍵點的影象塊,然而,高階豐富特徵(例如,SURF)考慮每一個特徵點的較高層次的資訊。使用光流或者豐富的特徵是設計師根據應用程式的輸入所做的決定。
找到相機矩陣——Finding camera matrices
既然我們獲得了兩個關鍵點之間的匹配,我們可以計算基礎矩陣並且從中獲得本徵矩陣。然而,我們必須首先調整我們的匹配點到兩個陣列,其中陣列中的索引對應於另外一個陣列中同樣的索引。這需要通過findFundametalMat函式獲得。我們可能也需要轉換KeyPoint 結構到Point2f結構。我們必須特別注意DMatch的queryIdx和trainIdx成員變數,在OpenCV中DMatch是容納兩個關鍵點匹配的結構,因為它們必須匹配我們使用matche.match()函式的方式。下面的程式碼部分展示瞭如何調整一個匹配到兩個相應的二維點集,以及如何使用它們來找到基礎矩陣:
vector<Point2f>imgpts1,imgpts2;
for( unsigned inti = 0; i<matches.size(); i++ )
{
// queryIdx is the "left" image
imgpts1.push_back(keypoints1[matches[i].queryIdx].pt);
// trainIdx is the "right" image
imgpts2.push_back(keypoints2[matches[i].trainIdx].pt);
}
Mat F = findFundamentalMat(imgpts1, imgpts2, FM_RANSAC, 0.1, 0.99,
status);
Mat_<double> E = K.t() * F * K; //according to HZ (9.12)稍後我們可能使用status二值向量來修剪這些點,使這些點和恢復的基礎矩陣匹配。看下面的影象:用來闡述使用基礎矩陣修剪後的點匹配。紅色箭頭表示特徵匹配在尋找基礎矩陣的過程中被移除了,綠色箭頭表示被保留的特徵匹配。

現在我們已經準備好尋找相機矩陣。這個過程在H和Z書的第九章進行了詳細的描述。然而,我們將使用一個直接和簡單的方法來實現它,並且OpenCV很容易的為我們做這件事。但是首先,我們將簡短地檢查我們將要使用的相機矩陣的結構:
我們的相機使用該模型,它由兩個成分組成,旋轉(表示為R)和平移(表示為t)。關於它的一個有趣的事情是它容納一個非常基本的等式:x=PX,這裡x是影象上的二維點,X是空間上的三維點。還有更多,但是這個矩陣給我們一個非常重要的關係,即影象中點和場景中點之間的關係。因此,既然我們有了尋找攝像機矩陣的動機,那麼我們將看到這個過程是怎麼完成的。下面的的程式碼部分展示瞭如何將本徵矩陣分解為旋轉和平移成分。
SVD svd(E);
Matx33d W(0,-1,0,//HZ 9.13
1,0,0,
0,0,1);
Mat_<double> R = svd.u * Mat(W) * svd.vt; //HZ 9.19
Mat_<double> t = svd.u.col(2); //u3
Matx34d P1( R(0,0),R(0,1), R(0,2), t(0),
R(1,0),R(1,1), R(1,2), t(1),
R(2,0),R(2,1), R(2,2), t(2));非常簡單。我們需要做的工作僅是對我們先前獲得的本徵矩陣進行奇異值分解(SVD),並且乘以一個特殊的矩陣W。對於我們所做的數學上的操作不進行過深地闡述,我們可以說SVD操作將我們的矩陣E分解成為兩部分,一個旋轉成分和一個平移成分。實時上,本徵矩陣起初是通過這兩個成分相乘構成的。完全地是滿足我們的好奇心,我們可以看下面的本徵矩陣的等式,它在字面意義上表現為:E=[t]xR(x是t的下標)。我可以看到它是由一個平移成分和一個旋轉成分組成。
我們注意到,我們所做的僅是得到了一個相機矩陣,因此另外一個相機矩陣呢?好的,我們在假定一個相機矩陣是固定的並且是標準的(沒有旋轉和平移)情況下進行這個操作。下一個矩陣(這裡的下一個矩陣表示相對於上面的P)也是標準的:
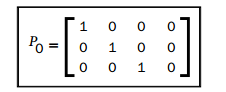
我們從本徵矩陣恢復的另外一個相機相對於固定的相機進行了移動和旋轉。這同樣意味著我們從這兩個相機矩陣中恢復的任何三維點都是擁有第一個相機在世界座標系中的原點(0,0,0)。
然而,這不是一個完全解。H和Z在他們的書中展示瞭如何和為什麼這樣的分解有四個可能的相機矩陣,但是僅有一個是正確的。正確的相機矩陣將產生帶有一個正Z值(點在攝像機的前面)的重構點。但是我們僅有當學了下一步將要討論的三角測量和3維重建之後才能理解。
還有一個我們可以考慮新增到我們的方法中的事情是錯誤檢測。多次從點的匹配中計算基礎矩陣是錯誤的,並影響相機矩陣。帶有錯誤相機矩陣的進行三角測量是毫無意義的。我們可以安裝一個檢查來檢測是否旋轉成分是一個有效的旋轉矩陣。牢記旋轉矩陣必須是一個行列式值為1(或者-1),我們可以簡單地進行如下做法:
bool CheckCoherentRotation(cv::Mat_<double>& R) {
if(fabsf(determinant(R))-1.0 > 1e-07) {
cerr<<"det(R) != +-1.0, this is not a rotation matrix"<<endl;
return false;
}
return true;
}
We can now see how all these elements combine into a function that recovers the P
matrices, as follows:
void FindCameraMatrices(const Mat& K,
const Mat& Kinv,
const vector<KeyPoint>& imgpts1,
const vector<KeyPoint>& imgpts2,
Matx34d& P,
Matx34d& P1,
vector<DMatch>& matches,
vector<CloudPoint>& outCloud
)
{
//Find camera matrices
//Get Fundamental Matrix
Mat F = GetFundamentalMat(imgpts1,imgpts2,matches);
//Essential matrix: compute then extract cameras [R|t]
Mat_<double> E = K.t() * F * K; //according to HZ (9.12)
//decompose E to P' , HZ (9.19)
SVD svd(E,SVD::MODIFY_A);
Mat svd_u = svd.u;
Mat svd_vt = svd.vt;
Mat svd_w = svd.w;
Matx33d W(0,-1,0,//HZ 9.13
1,0,0,
0,0,1);
Mat_<double> R = svd_u * Mat(W) * svd_vt; //HZ 9.19
Mat_<double> t = svd_u.col(2); //u3
if (!CheckCoherentRotation(R)) {
cout<<"resulting rotation is not coherent\n";
P1 = 0;
return;
}
P1 = Matx34d(R(0,0),R(0,1),R(0,2),t(0),
R(1,0),R(1,1),R(1,2),t(1),
R(2,0),R(2,1),R(2,2),t(2));
}此時,我們擁有兩個我們需要用來重建場景的相機。第一個相機是標準的,儲存在P變數中,第二個相機是我們計算得到的,構成基礎矩陣,儲存在P1變數中。下一部分我們將揭示如何使用這些相機來獲得場景的三維重建。
重構場景——Reconstructing the scene
接下來我們看一下從我們已經獲得的資訊中恢復場景的3D結構的事情。像先前所做的,我們應當看一下,用來完成這個事情我們手邊所擁有的工具和資訊。在前一部分,我們從本徵矩陣和矩陣矩陣中獲得了兩個相機矩陣。我們已經討論了這些工具用來獲得空間中一點的3D位置是如何的有用。那麼,我可以返回我們的匹配點來用資料填充等式。點對同樣對於計算我們獲得的近似計算的誤差有用。
現在我們看一些如何使用OpenCV執行三角測量。這次我們將會按照Tartley和Strum的三角測量的文章的步驟,文章中他們實現和比較了一些三角剖分的方法。我們將實現他們的線性方法的一種,因為使用OpenCv非常容易程式設計。
回憶一下,我們有兩個由2D點匹配和P矩陣產生的關鍵等式:x=PX和x’=P’X,x和x’是匹配的二維點,X是兩個相機進行拍照的真實世界三維點。如果我們重寫這個等式,我們可以公式化為一個線性方程系統,該系統可以解出X的值,X正是我們所期望尋找的值。假定X=(x,y,z,1)t(一個合理的點的假設,這些點離相機的中心不太近或者不太遠)產生一個形式為AX=B的非齊次線性方程系統。我們可以編碼和解決這個問題,如下:
Mat_<double> LinearLSTriangulation(
Point3d u,//homogenous image point (u,v,1)
Matx34d P,//camera 1 matrix
Point3d u1,//homogenous image point in 2nd camera
Matx34d P1//camera 2 matrix
)
{
//build A matrix
Matx43d A(u.x*P(2,0)-P(0,0),u.x*P(2,1)-P(0,1),u.x*P(2,2)-P(0,2),
u.y*P(2,0)-P(1,0),u.y*P(2,1)-P(1,1),u.y*P(2,2)-P(1,2),
u1.x*P1(2,0)-P1(0,0), u1.x*P1(2,1)-P1(0,1),u1.x*P1(2,2)-P1(0,2),
u1.y*P1(2,0)-P1(1,0), u1.y*P1(2,1)-P1(1,1),u1.y*P1(2,2)-P1(1,2)
);
//build B vector
Matx41d B(-(u.x*P(2,3)-P(0,3)),
-(u.y*P(2,3)-P(1,3)),
-(u1.x*P1(2,3)-P1(0,3)),
-(u1.y*P1(2,3)-P1(1,3)));
//solve for X
Mat_<double> X;
solve(A,B,X,DECOMP_SVD);
return X;
}我們將獲得由兩個2維點產生的3D點的一個近似。還有一個要注意的事情是,2D點用齊次座標表示,意味著x和y的值後面追加一個1。我們必須確保這些點在標準化的座標系中,這意味著它們必須乘以先前的標定矩陣K.我們可能注意到我們簡單地利用KP矩陣來替代k矩陣和每一個點相乘(每一點乘以KP),就是H和Z遍及第9章的做法那樣。我們現在可以寫一個關於點匹配的迴圈語句來獲得一個完整的三角測量,如下:
double TriangulatePoints(
const vector<KeyPoint>& pt_set1,
const vector<KeyPoint>& pt_set2,
const Mat&Kinv,
const Matx34d& P,
const Matx34d& P1,
vector<Point3d>& pointcloud)
{
vector<double> reproj_error;
for (unsigned int i=0; i<pts_size; i++) {
//convert to normalized homogeneous coordinates
Point2f kp = pt_set1[i].pt;
Point3d u(kp.x,kp.y,1.0);
Mat_<double> um = Kinv * Mat_<double>(u);
u = um.at<Point3d>(0);
Point2f kp1 = pt_set2[i].pt;
Point3d u1(kp1.x,kp1.y,1.0);
Mat_<double> um1 = Kinv * Mat_<double>(u1);
u1 = um1.at<Point3d>(0);
//triangulate
Mat_<double> X = LinearLSTriangulation(u,P,u1,P1);
//calculate reprojection error
Mat_<double> xPt_img = K * Mat(P1) * X;
Point2f xPt_img_(xPt_img(0)/xPt_img(2),xPt_img(1)/xPt_img(2));
reproj_error.push_back(norm(xPt_img_-kp1));
//store 3D point
pointcloud.push_back(Point3d(X(0),X(1),X(2)));
}
//return mean reprojection error
Scalar me = mean(reproj_error);
return me[0];
}在下面的影象中我們將看到一個兩個影象三角測量的結果。這兩個影象來至於P-11序列:
http://cvlab.epfl.ch/~strecha/multiview/denseMVS.html.
上面的兩個影象是原始場景的兩個檢視,下面的一對影象是從兩個檢視重構得到的點雲檢視,包含著估計相機朝向噴泉。我們可以看到右手邊紅色磚塊牆部分是如何重構的,並且也可以看到突出於牆的噴泉。

然而,像我們前面提到的那樣,關於重構存在著這樣的一個問題:重構僅能達到尺度上的。我們應當花一些時間來理解達到尺度(up-to-scale)的意思。我們獲得的兩個攝像機之間的運動存在一個隨意測量的單元,也就是說,它不是用釐米或者英寸,而是簡單地給出尺度單位。我們重構的相機將是尺度單元距離上的分開。這在很大程度上暗示我們應當決定過會重新獲得更多的相機,因為每一對相機都擁有各自的尺度單元,而不是一個一般的尺度。
現在我們將討論我們建立的誤差測量是如何可能的幫助我們來找到一個更加魯棒性的重構。首先,我們需要注意重投影意味著我們簡單地利用三角化的3D點並且將這些點重塑到相機上以獲得一個重投影的2D點。如果這個距離很大,這意味著我們在三角測量中存在一個誤差,因此,在最後的結果中,我們可能不想包含這個點。我們的全域性測量是平均重投影距離並且可能提供一個暗示——我們的三角剖分總體執行的怎麼樣。高的重投影率可能表明P矩陣存在問題,因此該問題可能是存在於本徵矩陣的計算或者匹配特徵點中。
我們應當簡短地回顧一下在前一部分我們討論的相機矩陣。我們提到相機矩陣P1的分解可以通過四個不同的方式進行分解,但是僅有一個分解是正確的。既然,我們知道如何三角化一個點,我們可以增加一個檢測來看四個相機矩陣中哪一個是有效地的。我們應當跳過在一點實現上的細節,因為它們是本書隨書例項程式碼中的精選(專題)。
下一步,我們將要看一下重新獲得直視場景的更多的相機,並且組合這些3D重建的結果。
從多檢視中重建——Reconstruction from many views
既然我們知道了如何從兩個相機中恢復運動和場景幾何,簡單地應用相同的過程獲得額外相機的引數和更多場景點似乎不重要。事實上,這件事並不簡單因為我們僅可以獲得一個達到尺度的重構,並且每對影象給我們一個不同的尺度。
有一些方法可以正確的從多個視場中重構3D場景資料。一個方法是後方交會(resection)或者相機姿態估計(camera pose estimation),也被稱為PNP(Perspective-N-Point),這裡我們將使用我們已經找到的場景點來解決一個新相機的位置。另外一個方法是三角化更多的點並且看它們是如何適應於我們存在的場景幾何的。憑藉ICP(Iterative Closest Point )我們可以獲得新相機的位置。在這一章,我們將討論使用OpenCV的sovlePnP函式來完成第一個方法。
第一步我們選擇這樣的重構型別即使用相機後方交會的增加的3D重構,來獲得一個基線場景結構。因為我們將基於一個已知的場景結構來尋找任何相機的位置,我們需要找到要處理的一個初始化的結構和一條基線。我們可以使用先前討論的方法——例如,在第一個視訊幀和第二個視訊幀之間,通過尋找相機矩陣(使用FindCameraMatrices函式)來獲得一條基線並且三角化幾何(使用TriangulatePoints函式)。
發現一個基礎結構後,我們可以繼續。然而,我們的方法需要相當多的資料記錄。首先,我們需要注意solvePnP函式需要兩個對齊的3D和2D點的向量。對齊的向量意味著一個向量的第i個位置與另外一個向量的第i位置對齊。為了獲得這些向量,我們需要在我們早前恢復的3D點中找到這些點,這些點與在我們新視訊幀下的2D點是對齊的。完成這個的一個簡單的方式是,對於雲中的每一個3D點,附加一個來至2D點的向量。然後我們可以使用特徵匹配來獲得一個匹配對。
讓我們為一個3D點引入一個新的結構,如下:
struct CloudPoint {
cv::Point3d pt;
std::vector<int>index_of_2d_origin;
};它容納,3D點和一個容器,容器內的元素為每幀影象上2D點的索引值,這些2D點用來計算3D點。當三角化一個新的3D點時,index_of_2d_origin的資訊必須被初始化,來記錄在三角化中哪些相機涉及到。然而,我們可以使用它來從我們的3D點雲追溯到每一幀上的2D點,如下:
std::vector<CloudPoint> pcloud; //our global 3D point cloud
//check for matches between i'th frame and 0'th frame (and thus the
current cloud)
std::vector<cv::Point3f> ppcloud;
std::vector<cv::Point2f> imgPoints;
vector<int> pcloud_status(pcloud.size(),0);
//scan the views we already used (good_views)
for (set<int>::iterator done_view = good_views.begin(); done_view !=
good_views.end(); ++done_view)
{
int old_view = *done_view; //a view we already used for
reconstrcution
//check for matches_from_old_to_working between
<working_view>'th frame and <old_view>'th frame (and thus
the current cloud)
std::vector<cv::DMatch> matches_from_old_to_working =
matches_matrix[std::make_pair(old_view,working_view)];
//scan the 2D-2D matched-points
for (unsigned int match_from_old_view=0;
match_from_old_view<matches_from_old_to_working.size();
match_from_old_view++) {
// the index of the matching 2D point in <old_view>
int idx_in_old_view =
matches_from_old_to_working[match_from_old_view].queryIdx;
//scan the existing cloud to see if this point from <old_view>
exists for (unsigned int pcldp=0; pcldp<pcloud.size(); pcldp++) {
// see if this 2D point from <old_view> contributed to this 3D
point in the cloud
if (idx_in_old_view == pcloud[pcldp].index_of_2d_origin[old_view]
&& pcloud_status[pcldp] == 0) //prevent duplicates
{
//3d point in cloud
ppcloud.push_back(pcloud[pcldp].pt);
//2d point in image <working_view>
Point2d pt_ = imgpts[working_view][matches_from_old_to_
working[match_from_old_view].trainIdx].pt;
imgPoints.push_back(pt_);
pcloud_status[pcldp] = 1;
break;
}
}
}
}
cout<<"found "<<ppcloud.size() <<" 3d-2d point correspondences"<<endl;現在,我們有一個場景中3D點到一個新視訊幀中2D點水平對齊對,我們可以使用他們重新得到相機的位置,如下:
cv::Mat_<double> t,rvec,R;
cv::solvePnPRansac(ppcloud, imgPoints, K, distcoeff, rvec, t, false);
//get rotation in 3x3 matrix form
Rodrigues(rvec, R);
P1 = cv::Matx34d(R(0,0),R(0,1),R(0,2),t(0),
R(1,0),R(1,1),R(1,2),t(1),
R(2,0),R(2,1),R(2,2),t(2));
既然我們正在使用sovlePnPRansac函式而不是sovlePnP函式,因為它對於異常值有更好的魯棒性。既然我們獲得了一個新的P1矩陣,我們可以簡單的再次使用我們早先定義的TriangualtePoints函式並且用更多的3D點來填充我們的3D點雲。
在下面的影象中,我們看到一個增加的噴泉場景的重構(訪問:http://cvlab.epfl.ch/~strecha/multiview/denseMVS.html,),從第四個影象。左上角的影象是使用了4個影象的重構;參加拍攝的相機用帶有白線的紅色簡單表示,箭頭表示了方向。其他的影象展示了更多 的相機來新增更多的點到點雲中。
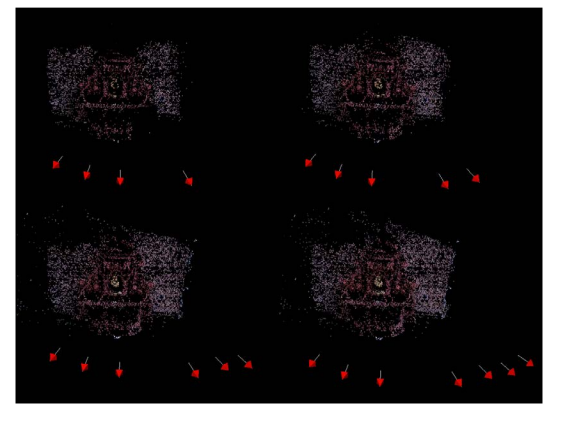
重構提純——Refinement of the reconstruction
SfM方法中最重要的一個部分是提純和最優化重構場景,通常被稱作BA過程(Bundle Adjustment)。這是一個優化步驟,這裡我們獲得的所有資料適應於一個統一的模型。3D點的位置和相機的位置都得到了最優化,因此重投影誤差最小(也就是說估計的3D點重投影到影象上接近於起源的2D點的位置)。這個過程通常需要解決帶有幾十千個引數指令的巨大的線性方程。這個過程可能會有些費力,但是我們前面採取的步驟允許帶有一個束調節(bundle adjuster)的簡單的整合。前面看起來奇怪的事情變的清晰了。例如,我們保留為點雲中的每一個3D點儲存原始的2D點的理由。
束調節的一個實現演算法是簡單稀疏束條調節SSBA(Simple Sparse Bundle Adjustment)庫。我們將選擇它作為我們的BA優化器, 因為它擁有簡單的API。它僅需要少量的輸入引數,這些輸入引數我們可以相當簡單的從我們的資料結構中建立。SSBA中我們使用的關鍵物件是CommonInternasMetricBundleOptimizer函式,這個函式執行最優化。它需要相機引數,3D點雲,點雲中每一個點相對應的2D影象點,以及直視場景的相機。到現在為止,利用這些引數應該很直接。我們應當注意這個BA方法假定所有影象通過同樣的硬體獲取,因此共同的內部,其他操作模式可能不需要假定這樣的情況。我們可以執行束調節(Bundle Adjustment),如下:
voidBundleAdjuster::adjustBundle(
vector<CloudPoint>&pointcloud,
const Mat&cam_intrinsics,
conststd::vector<std::vector<cv::KeyPoint>>&imgpts,
std::map<int ,cv::Matx34d>&Pmats
)
{
int N = Pmats.size(), M = pointcloud.size(), K = -1;
cout<<"N (cams) = "<< N <<" M (points) = "<< M <<" K (measurements) =
"<< K <<endl;
StdDistortionFunction distortion;
// intrinsic parameters matrix
Matrix3x3d KMat;
makeIdentityMatrix(KMat);
KMat[0][0] = cam_intrinsics.at<double>(0,0);
KMat[0][1] = cam_intrinsics.at<double>(0,1);
KMat[0][2] = cam_intrinsics.at<double>(0,2);
KMat[1][1] = cam_intrinsics.at<double>(1,1);
KMat[1][2] = cam_intrinsics.at<double>(1,2);
...
// 3D point cloud
vector<Vector3d >Xs(M);
for (int j = 0; j < M; ++j)
{
Xs[j][0] = pointcloud[j].pt.x;
Xs[j][1] = pointcloud[j].pt.y;
Xs[j][2] = pointcloud[j].pt.z;
}
cout<<"Read the 3D points."<<endl;
// convert cameras to BA datastructs
vector<CameraMatrix> cams(N);
for (inti = 0; i< N; ++i)
{
intcamId = i;
Matrix3x3d R;
Vector3d T;
Matx34d& P = Pmats[i];
R[0][0] = P(0,0); R[0][1] = P(0,1); R[0][2] = P(0,2); T[0] = P(0,3);
R[1][0] = P(1,0); R[1][1] = P(1,1); R[1][2] = P(1,2); T[1] = P(1,3);
R[2][0] = P(2,0); R[2][1] = P(2,1); R[2][2] = P(2,2); T[2] = P(2,3);
cams[i].setIntrinsic(Knorm);
cams[i].setRotation(R);
cams[i].setTranslation(T);
}
cout<<"Read the cameras."<<endl;
vector<Vector2d > measurements;
vector<int> correspondingView;
vector<int> correspondingPoint;
// 2D corresponding points
for (unsigned int k = 0; k <pointcloud.size(); ++k)
{
for (unsigned int i=0; i<pointcloud[k].imgpt_for_img.size(); i++) {
if (pointcloud[k].imgpt_for_img[i] >= 0) {
int view = i, point = k;
Vector3d p, np;
Point cvp = imgpts[i][pointcloud[k].imgpt_for_img[i]].pt;
p[0] = cvp.x;
p[1] = cvp.y;
p[2] = 1.0;
// Normalize the measurements to match the unit focal length.
scaleVectorIP(1.0/f0, p);
measurements.push_back(Vector2d(p[0], p[1]));
correspondingView.push_back(view);
correspondingPoint.push_back(point);
}
}
} // end for (k)
K = measurements.size();
cout<<"Read "<< K <<" valid 2D measurements."<<endl;
...
// perform the bundle adjustment
{
CommonInternalsMetricBundleOptimizeropt(V3D::FULL_BUNDLE_FOCAL_
LENGTH_PP, inlierThreshold, K0, distortion, cams, Xs, measurements,
correspondingView, correspondingPoint);
opt.tau = 1e-3;
opt.maxIterations = 50;
opt.minimize();
cout<<"optimizer status = "<<opt.status<<endl;
}
...
//extract 3D points
for (unsigned int j = 0; j <Xs.size(); ++j)
{
pointcloud[j].pt.x = Xs[j][0];
pointcloud[j].pt.y = Xs[j][1];
pointcloud[j].pt.z = Xs[j][2];
}
//extract adjusted cameras
for (int i = 0; i< N; ++i)
{
Matrix3x3d R = cams[i].getRotation();
Vector3d T = cams[i].getTranslation();
Matx34d P;
P(0,0) = R[0][0]; P(0,1) = R[0][1]; P(0,2) = R[0][2]; P(0,3) = T[0];
P(1,0) = R[1][0]; P(1,1) = R[1][1]; P(1,2) = R[1][2]; P(1,3) = T[1];
P(2,0) = R[2][0]; P(2,1) = R[2][1]; P(2,2) = R[2][2]; P(2,3) = T[2];
Pmats[i] = P;
}
}這個程式碼,雖然很長,是主要的關於轉換我們的內部資料結構到和來至SSBA的資料結構,並且呼叫最優化的過程。
下面的影象展示了BA的效果。左邊的兩個影象調整前的點雲中的點,來至兩個視角的觀察,並且右邊的影象展示了優化後的點雲。變化相當明顯,並且從不同檢視得到三角化點之間的不重合現在大部分統一了。我們同樣可以注意到調整建立了一個更好的平面重建。

使用PCL視覺化3D點雲——Visualizing 3D point clouds with PCL
當操作3D資料時,通過簡單地觀察重投影誤差測量或原始點資訊很難快速的理解結果是否正確。另一方面,如果我們觀察點雲(itself),我們可以立即的檢查這個點是否有意義或者存在誤差。為了視覺化,我們將使用一個很有前途的OpenCV的姊妹工程,稱為點雲庫(Point Cloud Librar)(PCL)。它帶有許多視覺化和分析點雲的工具,例如找到一個平面,匹配點雲,分割目標以及排除異常值。如果我們的目標不是一個點雲,而是一些高階資訊例如3D模型,這些工具將非常有用。
首先,我們需要在PCL的資料結構中表示我們的點雲(本質上是3D點的列表)。可以通過如下的做法實現:
pcl::PointCloud<pcl::PointXYZRGB>::Ptr cloud;
void PopulatePCLPointCloud(const vector<Point3d>& pointcloud,
const std::vector<cv::Vec3b>& pointcloud_RGB
)
//Populate point cloud
{
cout<<"Creating point cloud...";
cloud.reset(new pcl::PointCloud<pcl::PointXYZRGB>);
for (unsigned int i=0; i<pointcloud.size(); i++) {
// get the RGB color value for the point
Vec3b rgbv(255,255,255);
if (pointcloud_RGB.size() >= i) {
rgbv = pointcloud_RGB[i];
}
// check for erroneous coordinates (NaN, Inf, etc.)
if (pointcloud[i].x != pointcloud[i].x || isnan(pointcloud[i].x) ||
pointcloud[i].y != pointcloud[i].y || isnan(pointcloud[i].y) ||
pointcloud[i].z != pointcloud[i].z || isnan(pointcloud[i].z) ||
fabsf(pointcloud[i].x) > 10.0 ||
fabsf(pointcloud[i].y) > 10.0 ||
fabsf(pointcloud[i].z) > 10.0) {
continue;
}
pcl::PointXYZRGB pclp;
// 3D coordinates
pclp.x = pointcloud[i].x;
pclp.y = pointcloud[i].y;
pclp.z = pointcloud[i].z;
// RGB color, needs to be represented as an integer
uint32_t rgb = ((uint32_t)rgbv[2] << 16 | (uint32_t)rgbv[1] << 8 |
(uint32_t)rgbv[0]);
pclp.rgb = *reinterpret_cast<float*>(&rgb);
cloud->push_back(pclp);
}
cloud->width = (uint32_t) cloud->points.size(); // number of points
cloud->height = 1; // a list of points, one row of data
}為了視覺化有一個好的效果,我們也可以提供彩色資料如同影象中的RGB值。我們同樣也可以對原始點雲應用一個濾波器,這將消除可能是異常值的點,使用統計移除移除(statistical outlier removal)(SOR)工具如下:
Void SORFilter() {
pcl::PointCloud<pcl::PointXYZRGB>::Ptr cloud_filtered (new pcl::PointC
loud<pcl::PointXYZRGB>);
std::cerr<<"Cloud before SOR filtering: "<< cloud->width * cloud->height <<" data points"<<std::endl;
// Create the filtering object
pcl::StatisticalOutlierRemoval<pcl::PointXYZRGB>sor;
sor.setInputCloud (cloud);
sor.setMeanK (50);
sor.setStddevMulThresh (1.0);
sor.filter (*cloud_filtered);
std::cerr<<"Cloud after SOR filtering: "<<cloud_filtered->width *
cloud_filtered->height <<" data points "<<std::endl;
copyPointCloud(*cloud_filtered,*cloud);
}然後,我們可以使用PCL的API來執行一個簡單的點雲的視覺化器,如下:
Void RunVisualization(const vector<cv::Point3d>& pointcloud,
const std::vector<cv::Vec3b>& pointcloud_RGB) {
PopulatePCLPointCloud(pointcloud,pointcloud_RGB);
SORFilter();
copyPointCloud(*cloud,*orig_cloud);
pcl::visualization::CloudViewer viewer("Cloud Viewer");
// run the cloud viewer
viewer.showCloud(orig_cloud,"orig");
while (!viewer.wasStopped ())
{
// NOP
}
}下面的影象展示了統計移除移除工具(statistical outlier removal tool)使用之後的輸出結果。左手邊的影象是SfM的原始結果點雲。右手邊的影象展示經過SOR操作濾波之後的點雲。我們能夠注意到一些離群的點被移除了,剩下了一個更乾淨的點雲。

使用例項程式碼——Using the example code
我們可以在這本書提供的材料中找到SfM的例項程式碼。我們現在看一些怎麼樣編譯,執行和利用它。程式碼使用CMake,一個交叉編譯環境,類似於Maven或者SCons。我們同樣應當確保我們有下面的所有前提條件來編譯我們的應用程式:
• OpenCV v2.3 or highe• PCL v1.6 or higher
• SSBA v3.0 or higher
首先,我們必須建立編譯環境。為此,我們可能建立一個資料夾,命名為build,我們將所有編譯相關的檔案儲存在這裡。現在我們將假定所有的命令列操作都是在build/資料夾內,雖然這個過程是類似的(取決於檔案的位置),即使沒有使用build資料夾。
我們應當確保CMake可以找到SSBA和PCL,如果PCL正確的安裝了,那沒有問題。然而,我們必須通過-DSSBA_LIBRARY_DIR=...編譯引數設定正確的位置來找到SSBA的預編譯庫。如果我們正在使用Windows作業系統,我們可以使用Microsoft Visual Studio來編譯,因此,我們應當執行下面的的命令:
cmake –G "Visual Studio 10" -DSSBA_LIBRARY_DIR=../3rdparty/SSBA-3.0/
build/ ..如果我們使用Linux,Mac Os,或者其他Unix-Like作業系統,我們執行下面的命令:
cmake –G "Unix Makefiles" -DSSBA_LIBRARY_DIR=../3rdparty/SSBA-3.0/build/
..如果我們喜歡使用MacOS上的XCode,執行下面的命令:
cmake –G Xcode -DSSBA_LIBRARY_DIR=../3rdparty/SSBA-3.0/build/ ..CMake同樣可以為Eclipse,Codeblocks,和更多的環境編譯巨集命令。CMake完成建立編譯環境之後,我們準備編譯。如果我們正在使用一個Unix-like系統,我們可以簡單地執行這個生成工具(the make utility),否則我們應當使用我們開發環境的編譯過程。
編譯完成之後,我們應當獲得了一個執行程式名為ExploringSfMExex,這用來執行SfM過程。不帶引數執行這個程式會導致如下的顯示: USAGE: ./ExploringSfMExec <path_to_images>
為了在影象集上執行這個過程,我們應當提供位置作為驅動來找到影象檔案。如果提供了有效的位置,過程開始,我應當看到這個程式和螢幕上的除錯資訊。程式的結束將顯示源於影象的點雲。按1和2鍵,可以切換到調整的(adjusted)點雲和非調整的(non-adjusted)點雲。
總結——Summary
在這一章,我們已經看到了OpenCV是怎樣用一個既簡單編碼又好理解的方式來幫助我們處理來至運動的結構。OpenCV的API包含了一些有用的函式和資料結構,這使得我們生活的更加輕鬆,同樣地協助我們有一個更清潔的實現。
然而,最先進的SfM方法更復雜。那裡存在很多問題,我們選擇忽略,喜歡簡單化,以及在這些地方通常有更多的錯誤檢查。對於不同的SfM成分,我們選擇的方法同樣可以再次訪問。例如,H和Z提出了一個高精度的三角測量方法,甚至使用N-檢視三角測量,曾經他們利用多個影象理解特徵之間的關係。
如果我們想延伸和深化熟悉SfM,當然,我們將從觀察其他開源SfM庫中收益。一個特別感興趣的工程是libMV,它實現了大量的SfM成分,通過互換,這可能獲得最好的結果。華盛頓大學有一個偉大的作品,為很多型別SfM(Bundler and Visual SfM)提供了工具。這項作品的靈感來至於微軟的線上產品,稱作PhotoSynth。網上有很多容易訪問到的SfM的實現,並且一個人僅需來找到更多的SfM的實現。
我們沒有深入討論的另外一個重要的關係是SfM和視覺化定位以及對映,更好的稱為同步定位和對映(SLAM)方法。在這一章,我們已經處理給出的影象集和一個視訊序列,並且在這些情況下,使用SfM是可行的。然而,一些應用沒有預記錄的資料集並且必須動態時引導重建。這個過程被成為對映,並且當我們正在使用特徵匹配和2D跟蹤以及三角測量後來建立世界的3D對映時,這個過程被完成。
在下一章,我們將看到如何使用機器學習中的各種技術利用OpenCV從影象中提出車牌數字。
參考——References
• Multiple View Geometry in Computer Vision,Richard Hartley and Andrew
Zisserman,Cambridge University Press
• Triangulation, Richard I. Hartley and Peter Sturm, Computer vision and image
understanding, Vol. 68, pp. 146-157
• http://cvlab.epfl.ch/~strecha/multiview/denseMVS.html
• On Benchmarking Camera Calibration and Multi-View Stereo for High Resolution
Imagery,C. Strecha, W. von Hansen, L. Van Gool, P. Fua,and U. Thoennessen,
CVPR
• http://www.inf.ethz.ch/personal/chzach/opensource.html
• http://www.ics.forth.gr/~lourakis/sba/
• http://code.google.com/p/libmv/
• http://www.cs.washington.edu/homes/ccwu/vsfm/
• http://phototour.cs.washington.edu/bundler/
• http://photosynth.net/
• http://en.wikipedia.org/wiki/Simultaneous_localization_and_
mapping
• http://pointclouds.org
• http://www.cmake.org
相關文章
- 使用OpenCV和Python構建運動熱圖視訊OpenCVPython
- OpenCV訓練自己的衣服探測分類器OpenCV
- Video Division with using OpenCvIDEOpenCV
- 【OpenCV】OpenCV中GPU模組使用OpenCVGPU
- 用 Python 和 OpenCV 檢測和跟蹤運動物件PythonOpenCV物件
- Python-OpenCV 處理視訊(四): 運動檢測PythonOpenCV
- opencv SVM的使用OpenCV
- OpenCV矩陣運算OpenCV矩陣
- opencv 開運算、閉運算OpenCV
- Python+OpenCV目標跟蹤實現基本的運動檢測PythonOpenCV
- OpenCV(iOS)的邊緣檢測和Canny運算元OpenCViOS
- opencv SVM 使用OpenCV
- OpenCV 基本使用OpenCV
- OPENCV例程2 :CANNY運算元邊緣檢測OpenCV
- 混合高斯模型實現運動目標檢測(OpenCV內建實現)模型OpenCV
- 【python】OpenCV—findContours(4)PythonOpenCV
- OpenCV翻譯總結OpenCV
- Python-OpenCV 處理視訊(三)(四)(五): 標記運動軌跡 運動檢測 運動方向判斷PythonOpenCV
- opencv CvMLData的簡單使用OpenCVLDA
- Numpy 加法運算,opencv 加法運算,影像的融合OpenCV
- opencv 梯度運算、禮貌操作OpenCV梯度
- Reaction to 構造之法 of Software Engineering From The First Chapter toThe Fifth ChapterReactAPT
- opencv關鍵點檢測OpenCV
- 【opencv五】利用opencv給讀入的視訊新增拖動滑塊OpenCV
- 用樹莓派 + Python + OpenCV 實現家庭監控和移動目標探測(下)樹莓派PythonOpenCV
- 【OpenCV教程】OpenCV中的資料型別OpenCV資料型別
- OpenCV中GPU模組使用OpenCVGPU
- opencvOpenCV
- OpenCV()OpenCV
- 在Python中使用OpenCV進行人臉檢測PythonOpenCV
- 在Python中使用OpenCV訓練神經網路來檢測手勢!PythonOpenCV神經網路
- 【OpenCV教程】OpenCV中對矩陣的常用操作OpenCV矩陣
- GO語言學習筆記-包結構篇 Study for Go ! Chapter eight - Package StructureGo筆記APTPackageStruct
- opencv視訊人臉檢測OpenCV
- OpenCV 人臉檢測自學(3)OpenCV
- opencv-建立自己的角點檢測OpenCV
- OpenCV檢測篇(一)——貓臉檢測OpenCV
- OpenCV Core functionality翻譯總結OpenCVFunction
