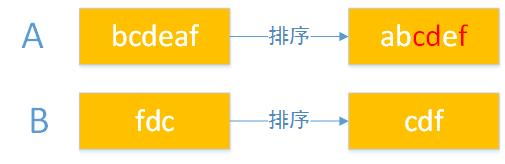
無順序約束的字串匹配問題

字串A較長，字串B較短，如何以最短時間判斷出B裡的所有字母在A中都有:？B⊆A

舉例：
A=abcdeabcdft，B=dcea，返回ture
若：B=dfgz，返回false

本題沒有字串順序約束，不需要保證B中字母在A出現的相對順序不變。下文幫助大家如何一步步優化匹配演算法。（有順序約束的字串匹配問題，請大家參考KMP演算法）
設len(A)=m,len(B)=n

• 最簡單的方法-輪詢O(m∗

  *
  n)

  輪詢字串B中的每個字母，看其是否在A中出現過。即判斷？Bi∈A

  ？B_i \in A
  。這種方法是最笨的方法，時間複雜度為O(m∗
  *
  n)，不可取。

• 先排序，再同時輪詢兩個字串O(mlogm

  mlog^m
  )

  可以先對兩個字串按字典排序，然後在A中找到和B相同的起始位置，同時進行輪詢。此時時間複雜度分類兩段：
  排序：O(nlogn

  log^n
  +mlogm
  log^m
  )（一般排序）
  輪詢：O(m+n)
  整體是mlogm
  mlog^m
  的時間複雜度，如果排序使用O(m)的方法就另說。
  

• 使用hashtable: O(α

  \alpha
  m+β
  \beta
  n)

  hashtable的優點是查詢時間為O(1)，故我們可以輪詢字串A，將其放在hashtable裡O(m)，然後輪詢字串B，在hashtable裡查詢每個字母Bi

  B_i
  ，看能否找到O(n)。這樣時間複雜度為O(m+n)，這是典型以空間換時間的做法。不過舉一個不太恰當的例子，若在hashtable裡字母a，b，c有相同的索引值，查詢時間就不是O(1)了，得加上key值比較的時間。說到這，大家是不是得去看看hashtable的工作原理啦。
  

• 利用素數-O(m+n)

  對於26個英文字母，給予每個字母分配一個素數，從2開始，往後類推。a:2, b:3, c:5, d:7 ⋯

  \cdots
  
  這樣，輪詢字串A，將每個字母代表的素數相乘，這樣會得到一個較大的數Big。然後輪詢字串B，若其字母代表的素數能被Big整除，就表示Bi⊆A
  B_i\subseteq A
  ，若有餘數返回false。即使字串A中有重複字母，仍然可以在O(m+n)時間複雜度內求得結果。