JAVA的六大經典演算法,程式碼案例簡化分析
java八大經典演算法:冒泡、選擇、快速、插入、希爾、堆、歸併、基數
1.演算法實現類
package com.algorithm;
/**
*
* @Title: BubbleSort.java
* @Copyright: Copyright (c) 2005
* @Description: <br>
* <br>
* JAVA六大經典演算法<br>
* 冒泡、選擇、快速、插入、希爾、堆
* @Created on 2015年6月29日 下午12:48:14
* @author yangkai
*/
public class AlgorithmClassic {
/**
* 氣泡排序
*
* @return
*/
public static int[] sortBubble(int[] datas) {
for (int i = 0; i < datas.length - 1; i++) {
for (int j = 0; j < datas.length - 1 - i; j++) {
if (datas[j] > datas[j + 1])
AlgorithmUtil.swap(datas, j, j + 1);
}
}
return datas;
}
/**
* 選擇排序
*
* @return
*/
public static int[] sortSelect(int[] datas) {
for (int i = 0; i < datas.length; i++) {
int index = i;
for (int j = i + 1; j < datas.length; j++) {
if (datas[j] < datas[index])
index = j;
}
if (i != index)
AlgorithmUtil.swap(datas, i, index);
}
return datas;
}
/**
* 插入排序法
*
* @param datas
*/
public static int[] sortInsert(int[] datas) {
for (int i = 1; i < datas.length; i++) {
int j = i - 1;
AlgorithmUtil.temp = datas[i];
for (; j >= 0 && AlgorithmUtil.temp < datas[j]; j--) {
datas[j + 1] = datas[j];
}
datas[j + 1] = AlgorithmUtil.temp;
}
return datas;
}
/**
* 快速排序;分割陣列
*
* @param datas
*/
public static int QuickPartition(int[] datas, int left, int right) {
int pivot = datas[left];
while (left < right) {
while (left < right && datas[right] >= pivot)
--right;
datas[left] = datas[right]; // 將比樞軸小的元素移到低端,此時right位相當於空,等待低位比pivotkey大的數補上
while (left < right && datas[left] <= pivot)
++left;
datas[right] = datas[left]; // 將比樞軸大的元素移到高階,此時left位相當於空,等待高位比pivotkey小的數補上
}
datas[left] = pivot; // 當left == right,完成一趟快速排序,此時left位相當於空,等待pivotkey補上
return left;
}
/**
* 快速排序;遞迴返回陣列
*
* @param datas
*/
public static int[] sortQuick(int[] datas, int left, int right) {
if (left < right) {
int data = QuickPartition(datas, left, right);
sortQuick(datas, left, data - 1);
sortQuick(datas, data + 1, right);
}
return datas;
}
}
2.演算法工具類
package com.algorithm;
public class AlgorithmUtil {
public static int temp,index = 0;
/**
* 臨時值交換
*
* @param datas
* 陣列
* @param i
* @param j
*/
public static void swap(int[] datas, int i, int j) {
temp = datas[i];
datas[i] = datas[j];
datas[j] = temp;
}
/**
* 擴充陣列長度
*
* @param datas
* @param value
* @return
*/
public static int[] expandArray(int[] datas, int value) {
if (datas.length <= index) {
int[] arrays = new int[datas.length * 2];
System.arraycopy(datas, 0, arrays, 0, datas.length);
datas = arrays;
}
datas[index] = value;
index++;
return datas;
}
}
3.重點演算法介紹
快速排序是所有排序演算法中效率最高最快的演算法,這裡重點介紹一下他的實現原理;
快速排序的基本思想:
通過一趟排序將待排序記錄分割成獨立的兩部分,其中一部分記錄的關鍵字均比另一部分關鍵字小,則分別對這兩部分繼續進行排序,直到整個序列有序。
資料一:
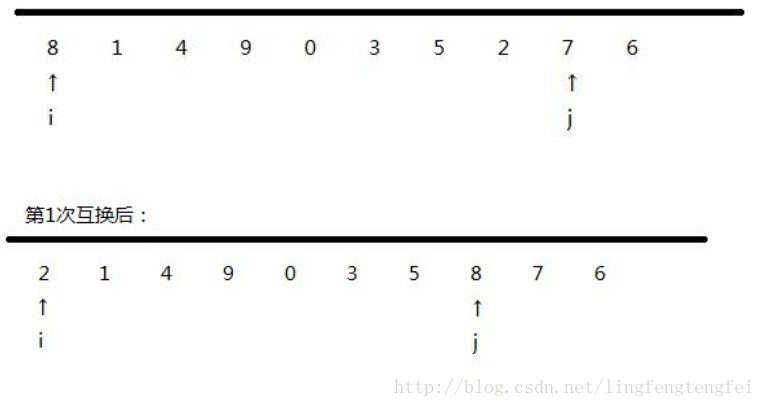
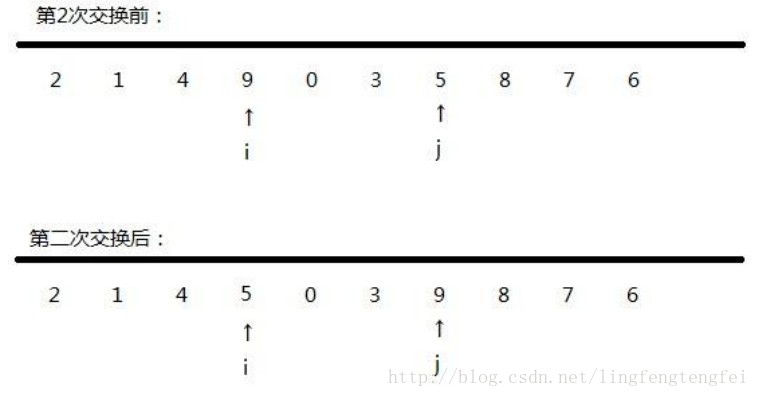
先看一下這幅圖:

把整個序列看做一個陣列,把第零個位置看做中軸,和最後一個比,如果比它小交換,比它大不做任何處理;交換了以後再和小的那端比,比它小不交換,比他大交換。這樣迴圈往復,一趟排序完成,左邊就是比中軸小的,右邊就是比中軸大的,然後再用分治法,分別對這兩個獨立的陣列進行排序。
資料二:
快速排序法事應用最廣泛的排序演算法之一,最佳情況下時間複雜度是 O(nlogn)。但是最壞情況下可能達到O(n^2)。說明快速排序達到最壞情況的原因。並提出改善方案並實現之。答:
改進方案:改進選取樞軸的方法
1、選取隨機數作為樞軸。
但是隨機數的生成本身是一種代價,根本減少不了演算法其餘部分的平均執行時間。
2、使用左端,右端和中心的中值做為樞軸元。
經驗得知,選取左端,右端,中心元素的中值會減少了快排大約 14%的比較。
3、每次選取資料集中的中位數做樞軸。
選取中位數的可以在 O(n)時間內完成。(證明見《演算法導論(第二版) 》) P111 第九章中位數
和順序統計學:在平均情況下,任何順序統計量(特別是中位數)都可以線上性時間內得到。
快排的分割策略:
第一步是通過將樞軸元與最後一個元素交換使得樞軸元離開要被分割的資料段;i 從第一個
元素開始而 j 從倒數第二個元素開始。當 i 在 j 左邊時,我們將 i 右移,移過那些小於樞軸
元的元素,並將 j 左移,移過那些大於樞軸元的元素。當 i 和 j 停止時,i 指向的是大元素,
j指向的是小元素。如果 i 在 j 左邊,那麼將這兩個元素互換。 如果此時 i 和 j 已經交錯即 i>j
所以不交換。此時把樞軸元與 i 所指的元素交換。
例項演示:
4.網上一些關於java演算法不錯的文章
http://www.cnblogs.com/liuling/p/2013-7-24-01.html
http://android.blog.51cto.com/268543/130450/
http://blog.csdn.net/hguisu/article/details/7776068
相關文章
- MySQL經典案例分析MySql
- Java 經典演算法分析總彙Java演算法
- 25道經典Java演算法題(含程式碼)Java演算法
- Java基礎經典案例Java
- 【Java】經典示例程式碼Java
- Linux 【Shell指令碼經典案例】Linux指令碼
- 化繁為簡 經典的漢諾塔遞迴問題 in Java遞迴Java
- 案例分析之JavaScript程式碼優化JavaScript優化
- 十大經典排序演算法動畫解析和 Java 程式碼實現排序演算法動畫Java
- 經典n皇后問題java程式碼實現Java
- JavaScript經典案例(二)JavaScript
- 【中亦安圖】Systemstate Dump分析經典案例(7)
- 【中亦安圖】Systemstate Dump分析經典案例(8)
- 30個關於Shell指令碼的經典案例(中)指令碼
- 30個關於Shell指令碼的經典案例(下)指令碼
- 30個關於Shell指令碼的經典案例(上)指令碼
- 十大經典排序演算法最強總結(含JAVA程式碼實現)排序演算法Java
- Java程式碼簡化神器-LombokJavaLombok
- Python學習之如何簡化程式碼?六大技巧!Python
- 經典排序演算法及其 Java 實現排序演算法Java
- 如何用簡易程式碼自動生成經典語錄
- C# 一句很簡單而又很經典的程式碼C#
- 經典T-SQL程式碼SQL
- 程式語言入門經典案例【Python版】Python
- java經典小程式:1、閏年Java
- 經典演算法演算法
- 經典排序演算法的 C語言 | Java 實現排序演算法C語言Java
- 10個經典的C語言面試基礎演算法及程式碼C語言面試演算法
- 經典氣泡排序的分析、優化及測試排序優化
- C++ 經典案例1例C++
- OpenCV之C++經典案例OpenCVC++
- 網頁廣泛使用的經典程式碼網頁
- java 介面回撥經典案例--網路請求回撥Java
- RC4演算法:流密碼演算法的經典之作演算法密碼
- 畫江湖之SQL優化 -10大經典案例場景SQL優化
- Lisp經典演算法Lisp演算法
- AQS:JAVA經典之鎖實現演算法(一)AQSJava演算法
- 目標函式的經典優化演算法介紹函式優化演算法