POJ 1039-Pipe（計算幾何-線段相交、求交點）

Description

The GX Light Pipeline Company started to prepare bent pipes for the new transgalactic light pipeline. During the design phase of the new pipe shape the company ran into the problem of determining how far the light can reach inside each component of the pipe. Note that the material which the pipe is made from is not transparent and not light reflecting. 

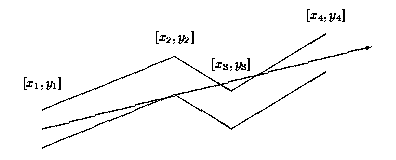
Each pipe component consists of many straight pipes connected tightly together. For the programming purposes, the company developed the description of each component as a sequence of points [x1; y1], [x2; y2], . . ., [xn; yn], where x1 < x2 < . . . xn . These are the upper points of the pipe contour. The bottom points of the pipe contour consist of points with y-coordinate decreased by 1. To each upper point [xi; yi] there is a corresponding bottom point [xi; (yi)-1] (see picture above). The company wants to find, for each pipe component, the point with maximal x-coordinate that the light will reach. The light is emitted by a segment source with endpoints [x1; (y1)-1] and [x1; y1] (endpoints are emitting light too). Assume that the light is not bent at the pipe bent points and the bent points do not stop the light beam.

Input

Output

Sample Input

4
0 1
2 2
4 1
6 4
6
0 1
2 -0.6
5 -4.45
7 -5.57
12 -10.8
17 -16.55
0

Sample Output

4.67
Through all the pipe.

Source

題目意思：

給出管道上半部分各個拐點處的座標（x,y），因為管道寬度為1，所以對應下半部分各個拐點處的座標是（x，y-1）。

有一道光線從管道最左邊射入，光線不能穿透管壁也不能拐彎，求解它是否能穿過這個管道，如果不可以，輸出到達管中位置的最大橫座標x。

解題思路：

先根據上下拐點的連線確定光線的入射斜率，列舉其與各個拐點的上下連線是否有交點，因為有交點則說明光線可以穿過該段管道。如果光線能夠穿過管道，那麼它將穿過每一段管道。

如果不能穿過，在第k節管道處無法穿過，則需要計算最大座標x：

分別計算與第k-1節管子的上、下管壁相交， 求得最大座標。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<iomanip>
using namespace std;
#define MAXN 30
const int INF=1e9;
const double eps=1e-3;
struct point
{
    double x,y;
};
int sgn(double p)//對double確定精度
{
    if(fabs(p)<eps)  return 0;
    return p>0?1:-1;
}
double circulation(point a,point b,point c)//計算向量BA、CA的叉積
{
    return (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
}
double dir(point A,point B,point P)//計算P點在AB的左側還是右側（AC與AB的螺旋關係）
{
    return circulation(A,B,P);
}
bool cross(point A,point B,point C,point D)//判斷線段AB和CD是否相交
{
    return (sgn(dir(A,B,C))*sgn(dir(A,B,D))<=0);
}
double intersection(point A,point B,point C,point D)//求AB與CD的交點x值
{
    double area1=dir(A,B,C);
    double area2=dir(A,B,D);
    int c=sgn(area1);
    int d=sgn(area2);
    if(c*d<0) //CD在AB的兩側，規範相交
        return (area2*C.x - area1*D.x)/(area2-area1);//交點計算公式
    if(c*d==0)   //CD的其中一個端點在AB上，不規範相交
    {
        if(c==0)
            return C.x;//C在AB上,返回AB與CD非規範相交時的交點C的橫座標
        else
            return D.x;//D在AB上,返回AB與CD非規範相交時的交點D的橫座標
    }
    return -INF; //CD在AB同側，無交點,返回負無窮
}
int main()
{
#ifdef ONLINE_JUDGE
#else
    freopen("F:/cb/read.txt","r",stdin);
    //freopen("F:/cb/out.txt","w",stdout);
#endif
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    while(cin>>n&&n)//n表示管道的數目
    {
        point p[MAXN],q[MAXN];
        for(int i=0; i<n; i++)
        {
            cin>>p[i].x>>p[i].y;
            q[i].x=p[i].x;
            q[i].y=p[i].y-1;
        }
        bool flag=false;
        double ans=-INF;
        int k;
        for(int i=0; i<n; i++)//列舉每段線段
        {
            for(int j=0; j<n; j++)
            {
                if(i==j) continue;
                for(k=0; k<n; k++)//列舉當前光線與第k個拐點處的上下連線是否相交
                    if(!cross(p[i],q[j],p[k],q[k]))//掃描到一個不相交
                        break;
                if(k>=n)//與每個拐點處都相交
                {
                    flag=true;
                    break;
                }
                else if(k>max(i,j))//不能穿過，求解最大x值
                {
                    double temp=intersection(p[i],q[j],p[k],p[k-1]);//求交點橫座標
                    if(ans<temp)//與第k-1節管子的上管壁相交
                        ans=temp;
                    temp=intersection(p[i],q[j],q[k],q[k-1]);
                    if(ans<temp)//與第k-1節管子的上管壁相交
                        ans=temp;
                }
            }
            if(flag)//可穿
                break;
        }
        if(flag)
            cout<<"Through all the pipe."<<endl;
        else
            cout<<fixed<<setprecision(2)<<ans<<endl;
    }
    return 0;
}
/*
4
0 1
2 2
4 1
6 4
6
0 1
2 -0.6
5 -4.45
7 -5.57
12 -10.8
17 -16.55
0
*/