藍橋杯-奪冠概率模擬（取隨機數）

    足球比賽具有一定程度的偶然性，弱隊也有戰勝強隊的可能。
    假設有甲、乙、丙、丁四個球隊。根據他們過去比賽的成績，得出每個隊與另一個隊對陣時取勝的概率表:
     甲   乙   丙   丁   
甲    -   0.1  0.3  0.5
乙  0.9   -    0.7  0.4 
丙  0.7   0.3  -    0.2
丁  0.5   0.6  0.8  -

    資料含義：甲對乙的取勝概率為0.1，丙對乙的勝率為0.3，...

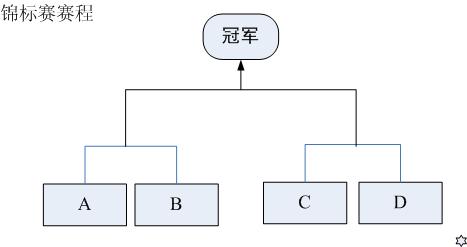
    現在要舉行一次錦標賽。雙方抽籤，分兩個組比，獲勝的兩個隊再爭奪冠軍。（參見【1.jpg】）

    請你進行10萬次模擬，計算出甲隊奪冠的概率。

    注意：

    請仔細除錯！您的程式只有能執行出正確結果的時候才有機會得分！
    

解題思路：

將所有組隊情況列舉出來，分3大類6小類計算出甲能取勝的概率：

double a=0.1*0.2*0.3+0.1*0.8*0.5;//預賽：甲乙、丙丁；決賽：甲vs丙/甲vs丁
double b=0.3*0.4*0.1+0.3*0.6*0.5;//預賽：甲丙、乙丁；決賽：甲vs乙/甲vs丁
double c=0.5*0.7*0.1+0.5*0.3*0.3;//預賽：甲丁、乙丙；決賽：甲vs乙/甲vs丙

然後在十萬次迴圈中，使用隨機數在0/1/2三個數中隨機取值，作為當前3個分組情況的模擬。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <ctime>
#include <algorithm>
using namespace std;
double arr[3];
/****
     甲   乙   丙   丁
甲    -   0.1  0.3  0.5
乙  0.9   -    0.7  0.4
丙  0.7   0.3  -    0.2
丁  0.5   0.6  0.8  -
****/
double a=0.1*0.2*0.3+0.1*0.8*0.5;//預賽：甲乙、丙丁；決賽：甲vs丙/甲vs丁
double b=0.3*0.4*0.1+0.3*0.6*0.5;//預賽：甲丙、乙丁；決賽：甲vs乙/甲vs丁
double c=0.5*0.7*0.1+0.5*0.3*0.3;//預賽：甲丁、乙丙；決賽：甲vs乙/甲vs丙
int main()
{
    int n=100000;//迴圈次數是十萬次
    double ans;
    int i;
    int c1,c2,c3;
    c1=c2=c3=0;
    srand(time(0));//需要用當前時間作“種子”，以便每次執行取得的序列不同
    while(n--)
    {
        i=rand()%3;  //產生0-10的隨機數
        //cout<<i;
        switch(i)
        {
        case 0:
            ans+=a;//++c1;
            break;
        case 1:
            ans+=b;//++c2;
            break;
        case 2:
            ans+=c;//++c3;
            break;
        }
    }
    //cout<<c1<<" "<<c2<<" "<<c3<<endl;
    cout<<ans/100000<<endl;
    return 0;
}
/*

*/