POJ 1523-SPF(Tarjan演算法-關節點)
SPF
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 8018 | Accepted: 3675 |
Description
Consider the two networks shown below. Assuming that data moves around these networks only between directly connected nodes on a peer-to-peer basis, a failure of a single node, 3, in the network on the left would prevent some of the still available nodes from
communicating with each other. Nodes 1 and 2 could still communicate with each other as could nodes 4 and 5, but communication between any other pairs of nodes would no longer be possible.
Node 3 is therefore a Single Point of Failure (SPF) for this network. Strictly, an SPF will be defined as any node that, if unavailable, would prevent at least one pair of available nodes from being able to communicate on what was previously a fully connected network. Note that the network on the right has no such node; there is no SPF in the network. At least two machines must fail before there are any pairs of available nodes which cannot communicate.
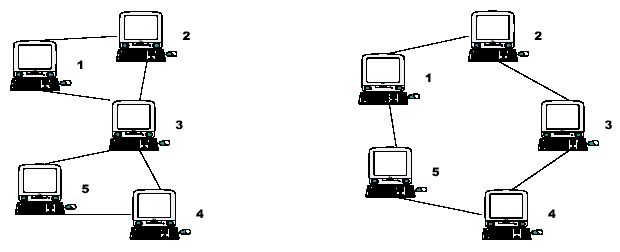
Node 3 is therefore a Single Point of Failure (SPF) for this network. Strictly, an SPF will be defined as any node that, if unavailable, would prevent at least one pair of available nodes from being able to communicate on what was previously a fully connected network. Note that the network on the right has no such node; there is no SPF in the network. At least two machines must fail before there are any pairs of available nodes which cannot communicate.

Input
The input will contain the description of several networks. A network description will consist of pairs of integers, one pair per line, that identify connected nodes. Ordering of the pairs is irrelevant; 1 2 and 2 1 specify the same connection. All node numbers
will range from 1 to 1000. A line containing a single zero ends the list of connected nodes. An empty network description flags the end of the input. Blank lines in the input file should be ignored.
Output
For each network in the input, you will output its number in the file, followed by a list of any SPF nodes that exist.
The first network in the file should be identified as "Network #1", the second as "Network #2", etc. For each SPF node, output a line, formatted as shown in the examples below, that identifies the node and the number of fully connected subnets that remain when that node fails. If the network has no SPF nodes, simply output the text "No SPF nodes" instead of a list of SPF nodes.
The first network in the file should be identified as "Network #1", the second as "Network #2", etc. For each SPF node, output a line, formatted as shown in the examples below, that identifies the node and the number of fully connected subnets that remain when that node fails. If the network has no SPF nodes, simply output the text "No SPF nodes" instead of a list of SPF nodes.
Sample Input
1 2 5 4 3 1 3 2 3 4 3 5 0 1 2 2 3 3 4 4 5 5 1 0 1 2 2 3 3 4 4 6 6 3 2 5 5 1 0 0
Sample Output
Network #1 SPF node 3 leaves 2 subnets Network #2 No SPF nodes Network #3 SPF node 2 leaves 2 subnets SPF node 3 leaves 2 subnets
Source
題目意思:
給出網路中兩兩節點連線的情況,求是否存在關節點,若存在,分成幾個聯通的子網路。
解題思路:
根據題目輸入建一個無向圖,然後用Tarjan演算法求解即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>
#include <map>
#include <algorithm>
using namespace std;
#define INF 0xfffffff
#define maxn 1010
int edge[maxn][maxn];//鄰接矩陣
int vis[maxn];//頂點訪問狀態
int n;//頂點數目
int tmpdfn;//dfs過程中記錄當前深度優先搜尋序數
int dfn[maxn];
int low[maxn];
int son;//根節點子女數(大於2為關節點)
int subnets[maxn];//每個節點(去掉該節點後的)連通分量數
void dfs(int u)//求得low
{
for(int v=1; v<=n; ++v)
if(edge[u][v])//u與v鄰接
{
if(!vis[v])//v未訪問,v是u的兒子節點
{
vis[v]=1;
++tmpdfn;
dfn[v]=low[v]=tmpdfn;
dfs(v);//low已經求得
low[u]=min(low[u],low[v]);//回退的時候,計算頂點u的low值
if(low[v]>=dfn[u])
{
if(u!=1) ++subnets[u];//去掉該節點後的連通分量數
if(u==1) ++son;//根節點子女數大於2為關節點
}
}
else low[u]=min(low[u],dfn[v]);//v已經訪問過,v是u的祖先節點,(v,u)是回邊
}
}
void init()//初始化
{
low[1]=dfn[1]=1;
tmpdfn=1;
son=0;
memset(vis,0,sizeof(vis));
vis[1]=1;
memset(subnets,0,sizeof(subnets));
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int i;
int u,v;//頂點對
int flag;//標誌是否找到
int ca=1;
while(1)
{
cin>>u;
if(u==0) break;//全部輸入結束
memset(edge,0,sizeof(edge));
n=0;
cin>>v;
if(u>n) n=u;
if(v>n) n=v;
edge[u][v]=edge[v][u]=1;
while(1)
{
cin>>u;
if(u==0) break;//當前組輸入結束
cin>>v;
if(u>n) n=u;
if(v>n) n=v;
edge[u][v]=edge[v][u]=1;
}
if(ca>1) puts("");//保證最後一個網路輸出置換木有空行
cout<<"Network #"<<ca++<<endl;
init();//初始化
dfs(1);//從頂點1開始DFS
if(son>1) subnets[1]=son-1;
flag=0;
for(i=1; i<=n; ++i)
if(subnets[i])
{
flag=1;
cout<<" SPF node "<<i<<" leaves "<<subnets[i]+1<<" subnets"<<endl;
}
if(!flag) puts(" No SPF nodes");
}
return 0;
}
/**
1 2
5 4
3 1
3 2
3 4
3 5
0
1 2
2 3
3 4
4 5
5 1
0
1 2
2 3
3 4
4 6
6 3
2 5
5 1
0
0
**/
相關文章
- POJ 1523 SPF (無向圖求割點 tarjan演算法)演算法
- POJ 2186 Popular Cows(強連通分量縮點,Tarjan演算法)演算法
- Tarjan演算法_縮點演算法
- tarjan演算法求scc & 縮點演算法
- POJ 1330 LCA最近公共祖先 離線tarjan演算法演算法
- POJ 3592 Instantaneous Transference 圖論演算法tarjan+spfa圖論演算法
- 強連通分量及縮點tarjan演算法解析演算法
- tarjan—演算法的神(一)演算法
- 強連通分量(Tarjan演算法)演算法
- 連通圖與Tarjan演算法演算法
- Tarjan 演算法學習筆記演算法筆記
- 【演算法學習】tarjan 強連通、點雙、邊雙及其縮點 重磅來襲!!!!演算法
- 圖論複習之強連通分量以及縮點—Tarjan演算法圖論演算法
- Tarjan(連通性相關) 筆記筆記
- Tarjan演算法(強連通分量分解)演算法
- POJ 基本演算法演算法
- 強連通------tarjan演算法詳解及與縮點聯合運用演算法
- 強連通分量與縮點(Tarjan演算法)(洛谷P3387)演算法
- 【模板】tarjan 強連通分量縮點
- poco節點關係大公開!
- 圖論——強連通分量(Tarjan演算法)圖論演算法
- Tarjan縮點題單 刷題題解
- POJ 3311 Hie with the Pie:TSP(旅行商)【節點可多次經過】
- Tarjan
- Tarjan演算法求強連通分量總結演算法
- 全網最!詳!細!Tarjan演算法講解。演算法
- 強連通分量-tarjan演算法模板詳解演算法
- 強連通演算法--Tarjan個人理解+詳解演算法
- 一文輕鬆搞定 tarjan 演算法(二)演算法
- 連通圖演算法詳解之① :Tarjan 和 Kosaraju 演算法演算法
- tarjan縮點-受歡迎的牛-筆記筆記
- tarjan[模板]
- 配置節點間的SSH信任關係
- kosaraju 和 tarjan演算法詳解(強連通分量)演算法
- 【Lca 離線Tarjan演算法】hdu 2586 How far away ?演算法
- Tarjan演算法三大應用之強連通分量演算法
- 替歸演算法獲取Treeview所有節點演算法View
- HDU 2767 Proving Equivalences Tarjan 強連通縮點UI