POJ 1149-PIGS（Ford-Fulkerson 標號法求網路最大流）

Mirko works on a pig farm that consists of M locked pig-houses and Mirko can't unlock any pighouse because he doesn't have the keys. Customers come to the farm one after another. Each of them has keys to some pig-houses and wants to buy a certain number of pigs. 
All data concerning customers planning to visit the farm on that particular day are available to Mirko early in the morning so that he can make a sales-plan in order to maximize the number of pigs sold. 
More precisely, the procedure is as following: the customer arrives, opens all pig-houses to which he has the key, Mirko sells a certain number of pigs from all the unlocked pig-houses to him, and, if Mirko wants, he can redistribute the remaining pigs across the unlocked pig-houses. 
An unlimited number of pigs can be placed in every pig-house. 
Write a program that will find the maximum number of pigs that he can sell on that day.

The first line of input contains two integers M and N, 1 <= M <= 1000, 1 <= N <= 100, number of pighouses and number of customers. Pig houses are numbered from 1 to M and customers are numbered from 1 to N. 
The next line contains M integeres, for each pig-house initial number of pigs. The number of pigs in each pig-house is greater or equal to 0 and less or equal to 1000. 
The next N lines contains records about the customers in the following form ( record about the i-th customer is written in the (i+2)-th line): 
A K1 K2 ... KA B It means that this customer has key to the pig-houses marked with the numbers K1, K2, ..., KA (sorted nondecreasingly ) and that he wants to buy B pigs. Numbers A and B can be equal to 0.

The first and only line of the output should contain the number of sold pigs.

3 3
3 1 10
2 1 2 2
2 1 3 3
1 2 6

7

Croatia OI 2002 Final Exam - First day

有M個豬圈，N個顧客，給出每個豬圈中豬的數目。

每個顧客有A把鑰匙，對應A個豬圈的編號，每個顧客會買B頭豬。

Mark木有豬圈的鑰匙，每個顧客來的時候把他們有鑰匙的豬圈全部開啟；而且Mark可以重新分配被開啟的豬圈裡面的豬。

顧客離開後，豬圈再次被鎖上。

求Mark能賣出的豬的最大值。

Ford-Fulkerson 標號法求網路最大流。

除了顧客的N個頂點外，自己增加源點和匯點這兩個點。

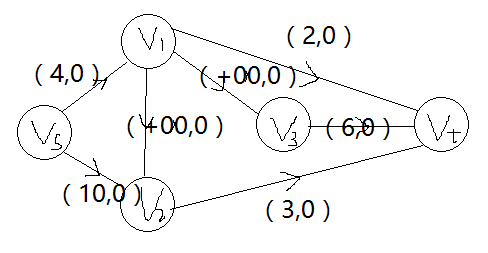
每個顧客購買的數目是連線到匯點上的容量；

源點與每個豬圈的第一個顧客連邊，邊的容量是開始時豬圈中豬的數目；

若源點與某個結點之間有重邊，將權合併（如上圖中Vs~V1，4就是合併了1和3）；

若顧客j緊跟i後面開啟豬圈，那麼<i，j>容量為正無窮（因為此時可以隨意調整豬圈中的豬的數量）。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <iomanip>
#include <algorithm>
#define maxn 1010
#define INF 0xfffffff
using namespace std;
struct ArcType
{
    int c,f;//容量、流量
};

ArcType edge[maxn][maxn];
int n,m;//頂點數、弧數
int s,t;
int flag[maxn];//頂點狀態：-1——未標號；0——已標號未檢查；1——已標號已檢查
int prev[maxn];//標號的第一個分量：指明標號從哪個頂點而來，以便找出可改進量
int alpha[maxn];//標號的第二個分量：可改進量α
int que[maxn];//相當於BFS中的佇列
int v;//佇列頭元素
int qs,qe;//隊首隊尾的位置
int i,j;

void ford()//標號法求網路最大流
{
    int flow[maxn][maxn];//節點之間的流量Fij
    int prev[maxn];//可改進路徑上前一個節點的標號，相當於標號的第一個分量
    int minflow[maxn];//每個頂點的可改進量α，相當於標號的第二個分量
    int que[maxn];
    int qs,qe;//佇列首尾位置座標
    int v,p;//當前頂點、儲存Cij-Fij
    for(i=0; i<maxn; ++i)
        for(j=0; j<maxn; ++j)
            flow[i][j]=0;
    minflow[0]=INF;//源點標號的第二分量為無窮大
    while(1)//標號法
    {
        for(i=0; i<maxn; ++i)//每次標號前，每個頂點重新回到未標號狀態
            prev[i]=-2;
        prev[0]=-1;
        qs=0;
        que[qs]=0;//源點入隊
        qe=1;
        while(qs<qe&&prev[t]==-2)
        {
            v=que[qs];//取佇列頭節點
            ++qs;
            for(i=0; i<t+1; ++i)//prev[i]==-2表示頂點i未標號
                if(prev[i]==-2&&(p=edge[v][i].c-flow[v][i]))//edge[v][i].c-flow[v][i]!=0能保證i是v鄰接頂點且能進行標號
                {
                    prev[i]=v;
                    que[qe]=i;
                    ++qe;
                    minflow[i]=(minflow[v]<p)?minflow[v]:p;
                }
        }
        if(prev[t]==-2) break;//匯點t無標號，標號法結束
        for(i=prev[t],j=t; i!=-1; j=i,i=prev[i])//調整過程
        {
            flow[i][j]+=minflow[t];
            flow[j][i]=-flow[i][j];
        }
    }
    for(i=0,p=0; i<t; ++i)//統計進入匯點的流量即最大流的流量
        p+=flow[i][t];
    cout<<p<<endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin>>m>>n;//頂點個數、弧數
    s=0,t=n+1;//源點和匯點
    int pig[maxn],last[maxn];//每個豬圈中豬的數量、每個豬圈前一個顧客的序號
    memset(last,0,sizeof(last));
    for(i=1; i<=m; ++i)
        cin>>pig[i];//輸入每個豬圈中豬的數量
    for(i=1; i<=n; ++i)
    {
        int num;
        cin>>num;//擁有的豬圈鑰匙數量
        for(j=0; j<num; ++j)
        {
            int k;
            cin>>k;//鑰匙編號
            if(last[k]==0)
                edge[s][i].c+=pig[k];
            else edge[last[k]][i].c=INF;
            last[k]=i;
        }
        cin>>edge[i][t].c;
        edge[i][t].f=0;
    }
    n+=2;//加上源點和匯點
    ford();
    return 0;
}
/*
3 3
3 1 10
2 1 2 2
2 1 3 3
1 2 6
*/