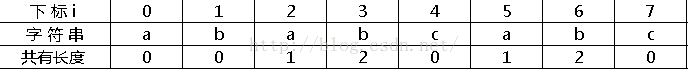KMP演算法的next、next value陣列的手工計算
昨天下午在書上看到了KMP演算法,看了很多很多很多遍都搞不懂什麼邏輯和原理;今天上午又聽了學長講了一遍感覺沒大聽懂,自己又上網找了很多相關文章,試了很多例子,終於找出來KMP演算法中手工計算next、next value陣列的方法了。下面我藉助網上的相關資料結合用我自己的思路說明一下。
一、什麼是字首字尾? 以字串s"ababcabc"為例:
"a"的字首和字尾都為空集,共有元素的長度為0;
"ab"的字首為[a],字尾為[b],共有元素的長度為0;
"aba"的字首為[a, ab],字尾為[ba, a],共有元素是【a】,長度為1;
"abab"的字首為[a, ab, aba],字尾為[bab, ab, b],共有元素是【ab】長度為2;
"ababc"的字首為[a, ab,aba, abab],字尾為[babc,abc, bc, c],共有元素長度為0;
"ababca"的字首為[a, ab,aba, abab,ababc],字尾為[babca,abca,bca, ca, a],共有元素是【a】,長度為1;
"ababcab"的字首為[a, ab,aba, abab,ababc,ababca],字尾為[babcab,abcab,bcab,cab, ab, b],共有元素是【ab】,長度為2;
"ababcabc"的字首為[a, ab,aba, abab,ababc,ababca,ababcab],字尾為[babcabc,abcabc,bcabc,cabc, abc, bc,c],共有元素的長度為0。
二、計算next陣列
把上面的共有長度按順序寫下來:
將“共有長度”全部整體向後移一位,首項為定值-1,得到next陣列:
三、計算next_value陣列
過程如下(next_value簡記為nv):
首先nv[0]=-1,是一個定值;
s[1]!=s[0],nv[1]=n[1]=0;
s[2]==s[0],nv[2]=nv[0]=-1;
s[3]==s[1],nv[3]=nv[1]=0;
s[4]!=s[2],nv[4]=n[4]=2;
s[5]==s[2],nv[5]=nv[2]=-1;
s[6]==s[3],nv[6]=nv[3]=0;
s[7]==s[4],nv[7]=nv[4]=2;
你們能找出規律嗎?
先將第二項與首項比較:若相同,nv值與首項相同;若不同,nv值等於n值。
如果前一次比較結果:若相同,與下一個字元進行比較;若不同,重複比較得出結果;
若比較結果是相同的情況:賦值的nv的下標依次遞加。
可能我表述的不太好,具體請看我上面的步驟,規律是顯而易見的。
綜上,就得到下面這張表:
相關文章
- KMP演算法的next、next value陣列程式碼實現及POJ3461KMP演算法陣列
- KMP演算法的Next陣列詳解KMP演算法陣列
- KMP演算法next陣列的深入理解KMP演算法陣列
- KMP演算法中關於next陣列的探究KMP演算法陣列
- 關於 KMP next 陣列的應用KMP陣列
- KMP演算法以及優化(程式碼分析以及求解next陣列和nextval陣列)KMP演算法優化陣列
- KMP演算法中我對獲取next陣列的理解KMP演算法陣列
- kmp 演算法簡介及 next 陣列推導KMP演算法陣列
- [資料結構]KMP演算法(含next陣列詳解)資料結構KMP演算法陣列
- POJ 2406-Power Strings(重複子串-KMP中的next陣列)KMP陣列
- BZOJ 3670 [Noi2014]動物園 (KMP next陣列應用)KMP陣列
- POJ 2752+KMP+利用next陣列性質求出所有相同的字首和字尾KMP陣列
- PHP 陣列current和next用法分享PHP陣列
- numpy——陣列的計算陣列
- 二維陣列的計算陣列
- 鴻蒙NEXT開發案例:年齡計算鴻蒙
- yield next和yield* next的區別
- 磁碟陣列可靠度的計算陣列
- 鴻蒙NEXT開發案例:血型遺傳計算鴻蒙
- 快速遷移 Next.js 應用到函式計算JS函式
- vue中的nextTickVue
- JS 獲取陣列物件的值&提取Object的valueJS陣列物件Object
- 陣列的位移運算陣列
- 淺談Abp vNext的模組化設計
- c語言中計算陣列長度的方法C語言陣列
- 計算兩個一維陣列的卷積陣列卷積
- C語言如何計算陣列的長度C語言陣列
- vue的nextTick的實現Vue
- jQuery next()jQuery
- 00022.08 Scanner的next()和nextLine()區別
- 往物件陣列裡面新增相同的key 不同的value物件陣列
- Vue中$nextTick的理解Vue
- MySQL 的next-lock 鎖MySql
- PHP陣列學習之計算陣列元素總和PHP陣列
- 一文帶你入木三分地理解字串KMP演算法(next指標解法)字串KMP演算法指標
- 陣列的基本演算法陣列演算法
- # Scanner:區別next和nextLine
- select multiple返回的value值是一個陣列陣列