Manacher-求最長迴文字串

轉載自：http://blog.sina.com.cn/s/blog_4a08aae90100ridt.html

題目描述：

     迴文串就是一個正讀和反讀都一樣的字串，比如“level”或者“noon”等等就是迴文串。       迴文子串，顧名思義，即字串中滿足迴文性質的子串。        給出一個只由小寫英文字元a,b,c...x,y,z組成的字串，請輸出其中最長的迴文子串的長度。

 

輸入：

     輸入包含多個測試用例，每組測試用例輸入一行由小寫英文字元a,b,c...x,y,z組成的字串，字串的長度不大於200000。

 

輸出：

     對於每組測試用例，輸出一個整數，表示該組測試用例的字串中所包含的的最長迴文子串的長度。

 

樣例輸入：

abab
bbbb
abba

樣例輸出：

3
4
4

思路：

 

      迴文串包括奇數長的和偶數長的，一般求的時候都要分情況討論，這個演算法做了個簡單的處理把奇偶情況統一了。原來是奇數長度還是奇數長度，偶數長度還是偶數長度。

      演算法的基本思路是這樣的，把原串每個字元中間用一個串中沒出現過的字元分隔#開來(統一奇偶)，同時為了防止越界，在字串的首部也加入一個特殊符$，但是與分隔符不同。同時字串的末尾也加入'\0'.

      演算法的核心：用輔助陣列p記錄以每個字元為核心的最長迴文字串半徑。也就是p[i]記錄了以str[i]為中心的最長迴文字串半徑。p[i]最小為1，此時迴文字串就是字串本身。

      先看個例子：

      原串：        w aa bwsw f d
      新串：     $ # w# a # a # b# w # s # w # f # d #
輔助陣列P：    1  2 1 2 3 2 1 2 1 2 1 4 1 2 1 2 1 2 1

 

#include <stdio.h>  
#include <iostream>
using namespace std;

char s[200002];  
char str[400010];  
int p[400010];  

int min(int a,int b){  
	return a < b ? a : b;  
}  

int pre(){  
	int i,j = 0;  
	str[j++] = '$';//加入字串首部的字串  
	for(i = 0;s[i];i++){  
		str[j++] = '#';  //分隔符
		str[j++] = s[i];  
	}  
	str[j++] = '#';  
	str[j] = '\0';  //尾部加'\0'
	cout<<str<<endl;
	return j;  
}  

void manacher(int n){  
	int mx = 0,id,i;  
	p[0] = 0;  
	for(i = 1;i < n;i++){  
		if(mx > i)  //在這個之類可以藉助前面算的一部分
			p[i] = min(mx - i,p[2 * id - i]); //p[2*id-1]表示j處的迴文長度 
		else  //如果i大於mx，則必須重新自己算
			p[i] = 1;  
		while(str[i - p[i]] == str[i + p[i]])  //算出迴文字串的半徑
			p[i]++;  
		if(p[i] + i > mx){  //記錄目前回文字串擴充套件最長的id
			mx = p[i] + i;  
			id = i;  
		}  
	}  
}  


int main(int argc, char const *argv[]){  

	while(scanf("%s",s) != EOF){  
		int n = pre();  
		manacher(n);  
		int ans = 0,i;  
		for(i = 1;i < n;i++)  
			if(p[i] > ans)  
				ans = p[i];  
		printf("%d\n",ans - 1);       
	}  
	return 0;  
} 

     上面的程式說明：pre()函式對給定字串進行預處理，也就是加分隔符。

 

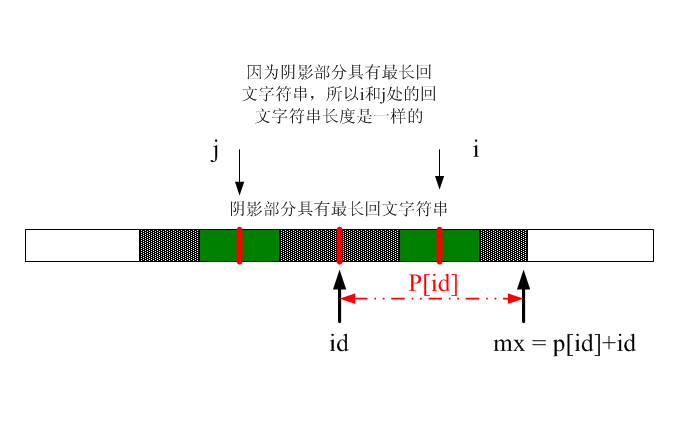
     上面幾個變數說明：id記錄具有遍歷過程中最長半徑的迴文字串中心字串。mx記錄了具有最長迴文字串的右邊界。看下面這個圖（注意，j為i關於id對稱的點，j = 2*id - i）：

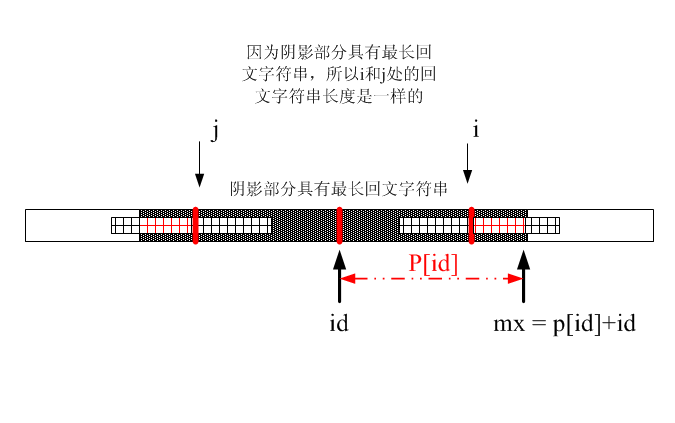
但是p[i] = p[j]是沒有錯的，但是這裡有個問題，就是i的一部分超出陰影部分，這就不對了。請看下圖（為了看得更清楚，下面子串用細條紋表示）：

      

其實核心的一句話就在於迴文翻轉了還是迴文這一句.

圖上也是在詮釋這一句,所以,利用前面已經匹配過的最大的迴文串,就是儘可能利用訪問過的資源

圖1中,以如果i大於mx的話,那麼就完全沒有前面的資訊可以用,只好乖乖的一個一個左右匹配,

但是如果i<mx的話,那麼就說明前面可以有相應的資源可以利用.因為以id的左右的迴文肯定包括i關於id對稱的j點處的一部分或者全部迴文.

所以如果是包括全部的話就是圖1的情況

如果只是包含部分的情況那麼就是圖2.

此時，根據對稱型只能得出p[i]和p[j]紅色陰影部分是相等的，這就為什麼有取最小值這個操作：

 

if(mx > i)  //在這個之類可以藉助前面算的一部分
    p[i] = min(mx - i,p[2 * id - i]);  

     下面程式碼就很容易看懂了。

      最後遍歷一遍p陣列，找出最大的p[i]-1就是所求的最長迴文字串長度，下面證明一下：

    （1）因為p[i]記錄插入分隔符之後的迴文字串半徑，注意插入分隔符之後的字串中的迴文字串肯定是奇數長度，所以以i為中心的迴文字串長度為2*p[i]-1。

例如：bb=>#b#b#

           bab=>#b#a#a#b#

    （2）注意上面兩個例子的關係。#b#b#減去一個#號的長度就是原來的2倍。即((2*p[i]-1)-1)/2 = p(i)-1，得證。

       演算法的有效比較次數為MaxId 次，所以說這個演算法的時間複雜度為O(n)。