【python資料探勘課程】二十.KNN最近鄰分類演算法分析詳解及平衡秤TXT資料集讀取
1.KNN演算法基礎原理知識
2.最近鄰分類演算法分析預測座標型別
3.Pandas讀取TXT資料集
4.KNN分析平衡秤資料集
5.演算法優化
本篇文章為基礎性文章,希望對你有所幫助,如果文章中存在錯誤或不足支援,還請海涵~同時,推薦大家閱讀我以前的文章瞭解基礎知識。自己真的太忙了,只能擠午休或深夜的時間學習新知識,但每次寫文內心都非常享受。
前文參考:
【Python資料探勘課程】一.安裝Python及爬蟲入門介紹
【Python資料探勘課程】二.Kmeans聚類資料分析及Anaconda介紹
【Python資料探勘課程】三.Kmeans聚類程式碼實現、作業及優化
【Python資料探勘課程】四.決策樹DTC資料分析及鳶尾資料集分析
【Python資料探勘課程】五.線性迴歸知識及預測糖尿病例項
【Python資料探勘課程】六.Numpy、Pandas和Matplotlib包基礎知識
【Python資料探勘課程】七.PCA降維操作及subplot子圖繪製
【Python資料探勘課程】八.關聯規則挖掘及Apriori實現購物推薦
【Python資料探勘課程】九.迴歸模型LinearRegression簡單分析氧化物資料
【python資料探勘課程】十.Pandas、Matplotlib、PCA繪圖實用程式碼補充
【python資料探勘課程】十一.Pandas、Matplotlib結合SQL語句視覺化分析
【python資料探勘課程】十二.Pandas、Matplotlib結合SQL語句對比圖分析
【python資料探勘課程】十三.WordCloud詞雲配置過程及詞頻分析
【python資料探勘課程】十四.Scipy呼叫curve_fit實現曲線擬合
【python資料探勘課程】十五.Matplotlib呼叫imshow()函式繪製熱圖
【python資料探勘課程】十六.邏輯迴歸LogisticRegression分析鳶尾花資料
【python資料探勘課程】十七.社交網路Networkx庫分析人物關係(初識篇)
【python資料探勘課程】十八.線性迴歸及多項式迴歸分析四個案例分享
【python資料探勘課程】十九.鳶尾花資料集視覺化、線性迴歸、決策樹花樣分析
一. KNN演算法基礎原理知識
K最近鄰(K-Nearest Neighbor,簡稱KNN)分類演算法是資料探勘分類技術中最簡單常用的方法之一。所謂K最近鄰,就是尋找K個最近的鄰居的意思,每個樣本都可以用它最接近的K個鄰居來代表。本小節主要講解KNN分類演算法的基礎知識及分析例項。
KNN分類演算法是最近鄰演算法,字面意思就是尋找最近鄰居,由Cover和Hart在1968年提出,簡單直觀易於實現。下面通過一個經典的例子來講解如何尋找鄰居,選取多少個鄰居。下圖是非常經典的KNN案例,需要判斷右邊這個動物是鴨子、雞還是鵝?它涉及到了KNN演算法的核心思想,判斷與這個樣本點相似的類別,再預測其所屬類別。由於它走路和叫聲像一隻鴨子,所以右邊的動物很可能是一隻鴨子。
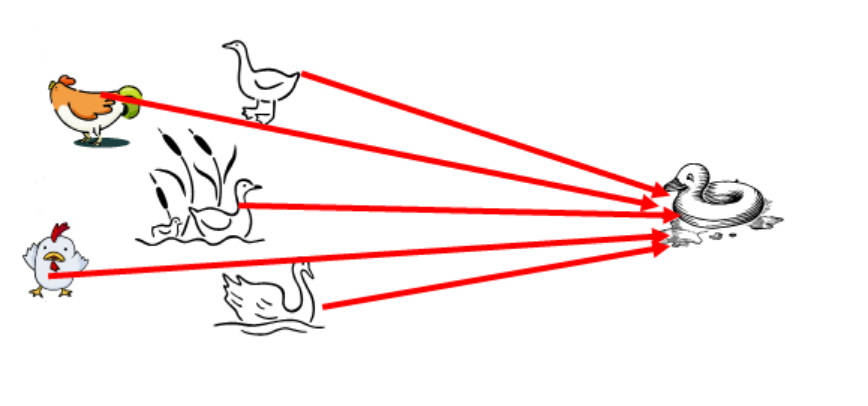
所以,KNN分類演算法的核心思想是從訓練樣本中尋找所有訓練樣本X中與測試樣本距離(歐氏距離)最近的前K個樣本(作為相似度),再選擇與待分類樣本距離最小的K個樣本作為X的K個最鄰近,並檢測這K個樣本大部分屬於哪一類樣本,則認為這個測試樣本類別屬於這一類樣本。
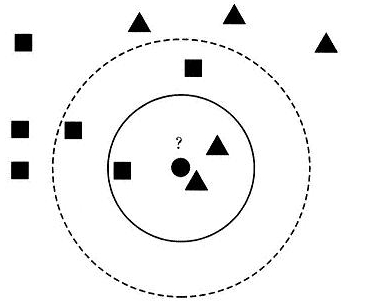
假設現在需要判斷下圖中的圓形圖案屬於三角形還是正方形類別,採用KNN演算法分析如下:
1.當K=3時,圖中第一個圈包含了三個圖形,其中三角形2個,正方形一個,該圓的則分類結果為三角形。
2.當K=5時,第二個圈中包含了5個圖形,三角形2個,正方形3個,則以3:2的投票結果預測圓為正方形類標。
總之,設定不同的K值,可能預測得到不同的結果。
二. 最近鄰分類演算法分析預測座標型別
KNN分類演算法的具體步驟如下:
1.計算測試樣本點到所有樣本點的歐式距離dist,採用勾股定理計算。
2.使用者自定義設定引數K,並選擇離帶測點最近的K個點。
3.從這K個點中,統計各個型別或類標的個數。
4.選擇出現頻率最大的類標號作為未知樣本的類標號,反饋最終預測結果。
KNN在Sklearn機器學習包中,實現的類是neighbors.KNeighborsClassifier,簡稱KNN演算法。構造方法為:
KNeighborsClassifier(algorithm='ball_tree',
leaf_size=30,
metric='minkowski',
metric_params=None,
n_jobs=1,
n_neighbors=3,
p=2,
weights='uniform')KNeighborsClassifier可以設定3種演算法:brute、kd_tree、ball_tree,設定K值引數為n_neighbors=3。
呼叫方法如下:
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=3, algorithm="ball_tree")
它也包括兩個方法:
訓練:nbrs.fit(data, target)
預測:pre = clf.predict(data)
下面這段程式碼是簡單呼叫KNN分類演算法進行預測的例子,程式碼如下。
# -*- coding: utf-8 -*-
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
X = np.array([[-1,-1],[-2,-2],[1,2], [1,1],[-3,-4],[3,2]])
Y = [0,0,1,1,0,1]
x = [[4,5],[-4,-3],[2,6]]
knn = KNeighborsClassifier(n_neighbors=3, algorithm="ball_tree")
knn.fit(X,Y)
pre = knn.predict(x)
print pre定義了一個二維陣列用於儲存6個點,其中x和y座標為負數的類標定義為0,x和y座標為正數的類標定義為1。呼叫knn.fit(X,Y)函式訓練模型後,再呼叫predict()函式預測[4,5]、[-4,-3]、[2,6]三個點的座標,輸出結果分別為:[1, 0, 1],其中x和y座標為正數的劃分為一類,負數的一類。
解釋:它相當於分別計算[4,5]點到前面X變數六個點的距離,採用歐式距離,然後選擇前3個(K=3)最近距離的點,看這三個點中屬於0和1類的個數,則該[4,5]點預測的型別則屬於較多的那個類別,即為1(正數)。
同時也可以計算K個最近點的下標和距離,程式碼和結果如下,返回距離k個最近的點和距離指數,indices可以理解為表示點的下標,distances為距離。
distances, indices = knn.kneighbors(X)
print indices
print distances
>>>
[1 0 1]
[[0 1 3]
[1 0 4]
[2 3 5]
[3 2 5]
[4 1 0]
[5 2 3]]
[[ 0. 1.41421356 2.82842712]
[ 0. 1.41421356 2.23606798]
[ 0. 1. 2. ]
[ 0. 1. 2.23606798]
[ 0. 2.23606798 3.60555128]
[ 0. 2. 2.23606798]]
>>> KNN分類演算法存在的優點包括:演算法思路較為簡單,易於實現;當有新樣本要加入訓練集中時,無需重新訓練,即重新訓練的代價低;計算時間和空間線性於訓練集的規模。
其缺點主要表現為分類速度慢,由於每次新的待分樣本都必須與所有訓練集一同計算比較相似度,以便取出靠前的K個已分類樣本。整個演算法的時間複雜度可以用O(m*n)表示,其中m是選出的特徵項(屬性)的個數,而n是訓練集樣本的個數。同時,各屬性的權重相同,影響了準確率,K值不好確定等會影響實驗結果。
下面通過一個完整的例項結合視覺化技術進行講解,加深同學們的印象。
三. Pandas讀取TXT資料集
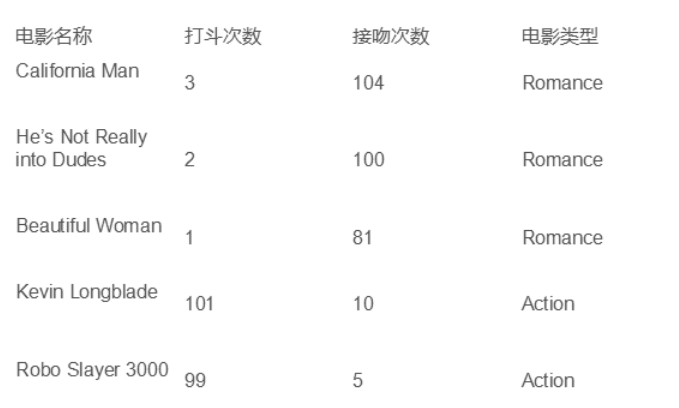
作者最早想分析電影資訊,如下圖所示,根據電影中出現的打鬥次數或親吻次數來判斷電影的型別,是屬於動作片、愛情片還是科幻片,但是無賴資料集不好構造,這裡修改為KNN分析平衡表資料集,但是其分析原理都是類似的,希望對您有所幫助。
該資料集者來自於UCI網路公開資料集,成為Balance Scale Dataset平衡表資料集。
下載地址為:http://archive.ics.uci.edu/ml/datasets/Balance+Scale。
資料集主要來自於平衡秤的重量和距離相關資料,共625個樣本,4個特徵。這個資料集被生成來模擬心理實驗結果。每個例子被分類為具有平衡尺度尖端向右,向左傾斜或平衡。屬性是左側重量,左側距離,右側重量和右側距離。找到類的正確方法是(左距離*左權重)和(右距離*右權重)中的較大者。如果他們平等,就是平衡的。
屬性如下表所示:
下載資料集至本地data.txt檔案,如下圖所示。
這裡作者採用Numpy擴充套件包中loadtxt()函式讀取data.txt檔案,注意資料集中每行資料都是採用逗號進行分割。
# -*- coding: utf-8 -*-
import os
import numpy as np
data = np.loadtxt("wine.txt",dtype=float,delimiter=",")
print data輸出內容如下所示,可以發現已經將資料讀取並儲存至data變數中。
[['B' '1' '1' '1' '1']
['R' '1' '1' '1' '2']
['R' '1' '1' '1' '3']
...,
['L' '5' '5' '5' '3']
['L' '5' '5' '5' '4']
['B' '5' '5' '5' '5']]由於資料中存在“B”、“R”、“L”三類字母,故需要轉換為字元型別(string)。同時該資料集存在一個特點,第一列為類標,後面四列為對應的資料集,則使用split()劃分第一列和剩餘4列資料,程式碼如下:
# -*- coding: utf-8 -*-
import os
import numpy as np
data = np.loadtxt("wine.txt",dtype=float,delimiter=",")
print data
yy, x = np.split(data, (1,), axis=1)
print yy.shape, x.shape
print x
print yy[:5] 輸出如下所示:
(625L, 1L) (625L, 4L)
[['1' '1' '1' '1']
['1' '1' '1' '2']
['1' '1' '1' '3']
...,
['5' '5' '5' '3']
['5' '5' '5' '4']
['5' '5' '5' '5']]
[['B']
['R']
['R']
['R']
['R']]同時這裡的類標為“B”、“R”、“L”,我也將其轉換為數字,其中“L”表示0,“B”表示1,“R”表示2。
程式碼如下:
#從字元型轉換為Int整型
X = x.astype(int)
print X
#字母轉換為數字
y = []
i = 0
print len(yy)
while i<len(yy):
if yy[i]=="L":
y.append(0)
elif yy[i]=="B":
y.append(1)
elif yy[i]=="R":
y.append(2)
i = i + 1
print y[:5]輸出內容如下所示,現在可以直接使用X陣列和y陣列進行KNN演算法分析。
[[1 1 1 1]
[1 1 1 2]
[1 1 1 3]
...,
[5 5 5 3]
[5 5 5 4]
[5 5 5 5]]
625
[1, 2, 2, 2, 2]四. KNN分析平衡秤資料集
接下來開始進行KNN演算法分類分析,其中KNN核心演算法主要步驟包括五步:
1.為了判斷未知例項的類別,以所有已知類別的例項為參照
2.選擇引數K
3.計算未知例項與所有已知例項的距離
4.選擇最近K個已知例項
5.根據少數服從多數的投票法則,讓未知例項歸類為K個最近鄰樣本中最多數的類標
呼叫SKlearn機器學習擴充套件包的核心程式碼如下所示:
from sklearn import neighbors
knn = neighbors.KNeighborsClassifier()
print knn輸出演算法原型如下:
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=5, p=2,
weights='uniform')
接下來呼叫fit()函式對資料集進行訓練,再呼叫predict函式對資料集進行預測,完整程式碼如下所示:
# -*- coding: utf-8 -*-
import os
import numpy as np
data = np.loadtxt("data.txt",dtype=str,delimiter=",")
print data
print type(data)
yy, x = np.split(data, (1,), axis=1)
print yy.shape, x.shape
print x
print yy[:5]
#從字元型轉換為Int整型
X = x.astype(int)
print X
#字母轉換為數字
y = []
i = 0
print len(yy)
while i<len(yy):
if yy[i]=="L":
y.append(0)
elif yy[i]=="B":
y.append(1)
elif yy[i]=="R":
y.append(2)
i = i + 1
print y[:5]
#KNN分析
from sklearn import neighbors
knn = neighbors.KNeighborsClassifier()
print knn
knn.fit(X,y)
pre = knn.predict(X)
print pre
#視覺化分析
import matplotlib.pyplot as plt
L1 = [x[0] for x in X]
L2 = [x[2] for x in X]
plt.scatter(L1, L2, c=pre, marker='s',s=200)
plt.show()
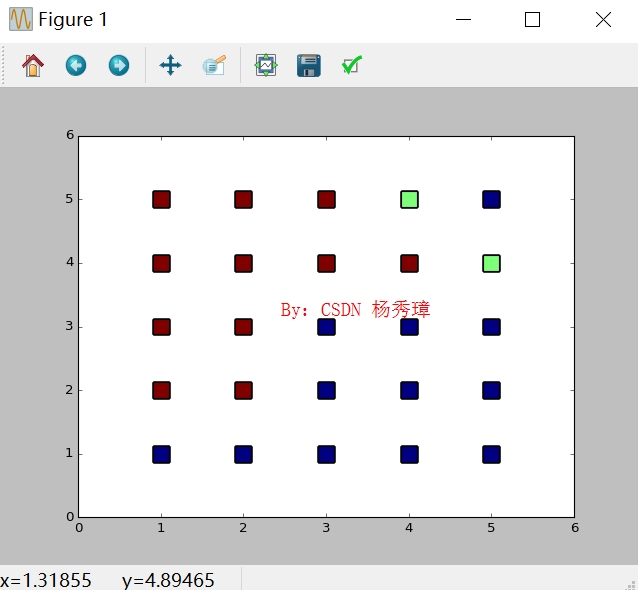
輸出預測結果如下所示,由於每列資料值為1到5,所以很多點出現重合。
最後簡單評價KNN演算法結果,程式碼如下:
#預測結果與真實結果比對
print sum(pre == y)
#輸出準確率 召回率 F值
from sklearn import metrics
print(metrics.classification_report(y,pre))
print(metrics.confusion_matrix(y,pre)) 輸出如圖所示圖形,其中625組資料中,共預測正確540組,Precision值為83%,召回率Recall為86%,F1特徵為84%,KNN演算法總體分析結果較好。
540
precision recall f1-score support
0 0.85 0.97 0.90 288
1 0.00 0.00 0.00 49
2 0.95 0.91 0.93 288
avg / total 0.83 0.86 0.84 625
[[279 4 5]
[ 41 0 8]
[ 10 17 261]]可以看到,該演算法的優點為易於理解,簡單容易實現,但是當資料量很大時,演算法的效率不是很理想。
五. 程式碼優化
最後提供一段優化後的程式碼,提取其中的兩列繪製相關的背景圖。
# -*- coding: utf-8 -*-
import os
import numpy as np
#第一步 匯入資料集
data = np.loadtxt("data.txt",dtype=str,delimiter=",")
print data
print type(data)
yy, x = np.split(data, (1,), axis=1)
print yy.shape, x.shape
#從字元型轉換為Int整型
X = x.astype(int)
#獲取x兩列資料,方便繪圖 對應x、y軸
X = X[:, 1:3]
print X
#字母轉換為數字
y = []
i = 0
print len(yy)
while i<len(yy):
if yy[i]=="L":
y.append(0)
elif yy[i]=="B":
y.append(1)
elif yy[i]=="R":
y.append(2)
i = i + 1
print y[:5]
#第二步 KNN分析
from sklearn import neighbors
knn = neighbors.KNeighborsClassifier()
print knn
knn.fit(X,y)
pre = knn.predict(X)
print pre
#第三步 資料評估
from sklearn import metrics
print sum(pre == y) #預測結果與真實結果比對
print(metrics.classification_report(y,pre)) #輸出準確率 召回率 F值
print(metrics.confusion_matrix(y,pre))
#第四步 建立網格
x1_min, x1_max = X[:,0].min()-0.1, X[:,0].max()+0.1 #第一列
x2_min, x2_max = X[:,1].min()-0.1, X[:,1].max()+0.1 #第二列
xx, yy = np.meshgrid(np.arange(x1_min, x1_max, 0.1),
np.arange(x2_min, x2_max, 0.1)) #生成網格型資料
print xx.shape, yy.shape #(42L, 42L) (42L, 42L)
print xx.ravel().shape, yy.ravel().shape #(1764L,) (1764L,)
print np.c_[xx.ravel(), yy.ravel()].shape #合併 (1764L, 2L)
#ravel()拉直函式
z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
print z
#第五步 繪圖視覺化
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF']) #顏色Map
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
plt.figure()
z = z.reshape(xx.shape)
plt.pcolormesh(xx, yy, z, cmap=cmap_light)
plt.scatter(X[:,0], X[:,1], c=y, cmap=cmap_bold, s=50)
plt.show()
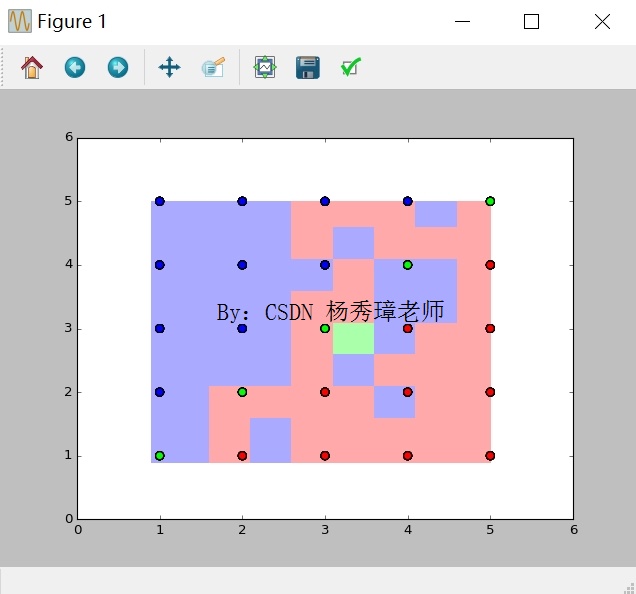
可以看到整個區域劃分為三種顏色,綠色區域、紅色區域和藍色區域。同時包括散點圖分佈,對應資料的類標,包括綠色、藍色和紅色的點。可以發現,相同顏色的點主要集中於該顏色區域,部分藍色點劃分至紅色區域或綠色點劃分至藍色區域,則表示預測結果與實際結果不一致。
感想雜談:
遇一人白首,擇一城終老。
經歷風雨,慢慢變老。
去年的今天,你提著蛋糕趕著公交,來到花溪,鼓起勇氣牽住了我的冰手; 今年的這天,你在緊急出差遵義前,準備蛋糕,送我驚喜,傾世溫柔。
很多人只看到了我的萬字情書,製作的視訊集錦,定期的狗糧,卻不知道你背後的關愛與付出,還有我的虧欠。謝謝這一年你給我的溫暖和安心,即使不在身邊,幾片文字,幾段聲音,搖首相望,也能感受到最純真的愛情。況且還有這麼多比韓劇還秀逗的劇情。來年我希望自己成長,學會擔當,學會取捨,撐起一個新的家庭。
回首,以前的秀璋真的很少講話,初中低頭走路上學,高中打不出一個屁來,大四畢業也才發了第一條說說,為什麼就改變呢? 確實,光靠我的勇氣,我可能還是那個悶不做聲的小屁娃,但你的勇氣和我的勇氣加起來,我們足夠應付整個世界,沒有遇見你,我哪來的勇氣,愛你就像愛生命。
PS: 失眠之夜,生日快樂。致大家: 一個人時,學會善待自己; 兩個人時,學會善待對方。
晚安,娜娜。晚安,貴陽。
希望文章對你有所幫助,尤其是我的學生,如果文章中存在錯誤或不足之處,還請海涵。
(By:Eastmount 2017-12-08 深夜12點 http://blog.csdn.net/eastmount/ )
相關文章
- 【python資料探勘課程】二十七.基於SVM分類器的紅酒資料分析Python
- 【python資料探勘課程】二十一.樸素貝葉斯分類器詳解及中文文字輿情分析Python
- 資料探勘——KNN演算法(手寫數字分類)KNN演算法
- 【python資料探勘課程】二十三.時間序列金融資料預測及Pandas庫詳解Python
- 【python資料探勘課程】二十四.KMeans文字聚類分析互動百科語料Python聚類
- 機器學習演算法-K近鄰(KNN)演算法(三):馬絞痛資料--kNN資料預處理+kNN分類pipeline(程式碼附詳細註釋)機器學習演算法KNN
- 【python資料探勘課程】十三.WordCloud詞雲配置過程及詞頻分析PythonCloud
- 【python資料探勘課程】二十五.Matplotlib繪製帶主題及聚類類標的散點圖Python聚類
- 《資料探勘導論》實驗課——實驗四、資料探勘之KNN,Naive BayesKNNAI
- 圖說十大資料探勘演算法(一)K最近鄰演算法大資料演算法
- 【python資料探勘課程】二十六.基於SnowNLP的豆瓣評論情感分析Python
- 萌新向Python資料分析及資料探勘 前言Python
- 【python資料探勘課程】十六.邏輯迴歸LogisticRegression分析鳶尾花資料Python邏輯迴歸
- 資料探勘(7):分類演算法評價演算法
- 【python資料探勘課程】二十二.Basemap地圖包安裝入門及基礎知識講解Python地圖
- 機器學習經典分類演算法 —— k-近鄰演算法(附python實現程式碼及資料集)機器學習演算法Python
- 【python資料探勘課程】十九.鳶尾花資料集視覺化、線性迴歸、決策樹花樣分析Python視覺化
- 資料探勘(6):決策樹分類演算法演算法
- 【Python資料探勘課程】九.迴歸模型LinearRegression簡單分析氧化物資料Python模型
- FCM聚類演算法詳解(Python實現iris資料集)聚類演算法Python
- Python資料探勘與分析速成班-CSDN公開課-專題視訊課程Python
- 《資料分析與資料探勘》--天津大學公開課
- 【Python資料探勘課程】七.PCA降維操作及subplot子圖繪製PythonPCA
- 【python資料探勘課程】十八.線性迴歸及多項式迴歸分析四個案例分享Python
- K-最近鄰法(KNN)簡介KNN
- 資料探勘資料集下載資源
- 資料探勘中分類演算法總結演算法
- 資料探勘十大演算法之Apriori詳解演算法
- 資料探勘的資料分析方法
- 【python資料探勘課程】十一.Pandas、Matplotlib結合SQL語句視覺化分析PythonSQL視覺化
- 【python資料探勘課程】十二.Pandas、Matplotlib結合SQL語句對比圖分析PythonSQL
- 資料探勘方向分析
- 手勢識別演算法: 資料濾波演算法、資料分演算法——KNN演算法KNN
- 資料探勘與分析 概念與演算法演算法
- python 資料探勘演算法簡要Python演算法
- HS系列USB資料採集卡,及高速多通道資料分析軟體詳解
- 資料探勘—邏輯迴歸分類—信用卡欺詐分析邏輯迴歸
- 資料分析與挖掘 - R語言:KNN演算法R語言KNN演算法