【python資料探勘課程】十六.邏輯迴歸LogisticRegression分析鳶尾花資料

Eastmount發表於2017-09-10
Python邏輯迴歸
今天是教師節，容我先感嘆下。
祝天下所有老師教師節快樂，這是自己的第二個教師節，這一年來，無限感慨，有給一個人的指導，有給十幾個人講畢設，有幾十人的實驗，有上百人的課堂，也有給上千人的Python網路直播。但每當站到講臺前，還是那麼興奮，那麼緊張，那麼享受，彷彿整個世界都是我的，很滿足。

站在講臺前的老師永遠是最美的，很榮幸能教導自己的每一個學生，很開心給每一個陌生網友和朋友解惑，這是緣分，應該珍惜；再苦再累，都覺得值當。最後還是祝所有同行教師節快樂，娜老師和璋老師，節日快樂！用離開北理選擇回來教書的那首詩結束。

《再見，北理工》
但行好事，莫問前程。
待隨滿天李桃，在追學友趣事。
別時到一句珍重，
不去思量，非常難忘。
無人可以訴衷腸，那又何妨。
留一段剪影，於心中回放。
幾十年生死，不也兩茫茫。


言歸正傳，前面第九篇文章作者介紹了線性迴歸相關知識，但是很多時候資料是非線性的，所以這篇文章主要講述邏輯迴歸及Sklearn機器學習包中的LogisticRegression演算法。希望文章對你有所幫助，如果文章中存在錯誤或不足之處，還請海涵~

前文推薦：
【Python資料探勘課程】一.安裝Python及爬蟲入門介紹
【Python資料探勘課程】二.Kmeans聚類資料分析及Anaconda介紹
【Python資料探勘課程】三.Kmeans聚類程式碼實現、作業及優化
【Python資料探勘課程】四.決策樹DTC資料分析及鳶尾資料集分析
【Python資料探勘課程】五.線性迴歸知識及預測糖尿病例項
【Python資料探勘課程】六.Numpy、Pandas和Matplotlib包基礎知識
【Python資料探勘課程】七.PCA降維操作及subplot子圖繪製
【Python資料探勘課程】八.關聯規則挖掘及Apriori實現購物推薦
【Python資料探勘課程】九.迴歸模型LinearRegression簡單分析氧化物資料
【python資料探勘課程】十.Pandas、Matplotlib、PCA繪圖實用程式碼補充
【python資料探勘課程】十一.Pandas、Matplotlib結合SQL語句視覺化分析
【python資料探勘課程】十二.Pandas、Matplotlib結合SQL語句對比圖分析
【python資料探勘課程】十三.WordCloud詞雲配置過程及詞頻分析
【python資料探勘課程】十四.Scipy呼叫curve_fit實現曲線擬合
【python資料探勘課程】十五.Matplotlib呼叫imshow()函式繪製熱圖


一. 邏輯迴歸

在前面講述的迴歸模型中，處理的因變數都是數值型區間變數，建立的模型描述是因變數的期望與自變數之間的線性關係。比如常見的線性迴歸模型：

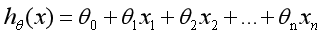
而在採用迴歸模型分析實際問題中，所研究的變數往往不全是區間變數而是順序變數或屬性變數，比如二項分佈問題。通過分析年齡、性別、體質指數、平均血壓、疾病指數等指標，判斷一個人是否換糖尿病，Y=0表示未患病，Y=1表示患病，這裡的響應變數是一個兩點（0-1）分佈變數，它就不能用h函式連續的值來預測因變數Y（只能取0或1）。
總之，線性迴歸模型通常是處理因變數是連續變數的問題，如果因變數是定性變數，線性迴歸模型就不再適用了，需採用邏輯迴歸模型解決。

邏輯迴歸（Logistic Regression）是用於處理因變數為分類變數的迴歸問題，常見的是二分類或二項分佈問題，也可以處理多分類問題，它實際上是屬於一種分類方法。
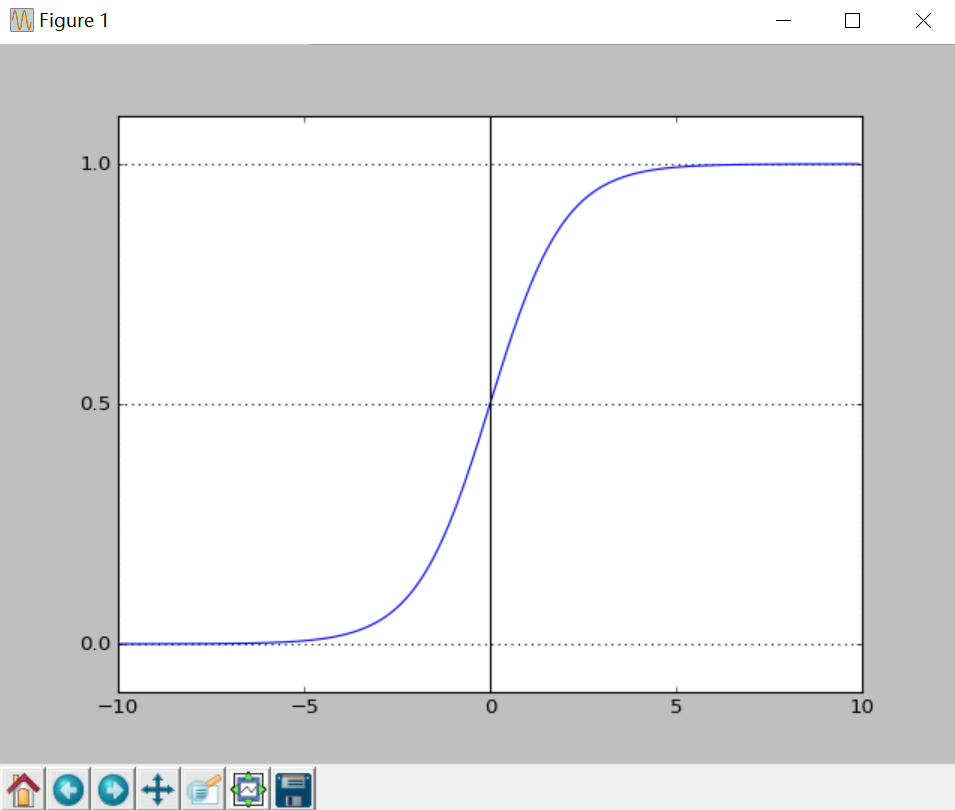
二分類問題的概率與自變數之間的關係圖形往往是一個S型曲線，如圖所示，採用的Sigmoid函式實現。



這裡我們將該函式定義如下：



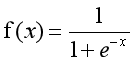
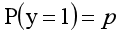
函式的定義域為全體實數，值域在[0,1]之間，x軸在0點對應的結果為0.5。當x取值足夠大的時候，可以看成0或1兩類問題，大於0.5可以認為是1類問題，反之是0類問題，而剛好是0.5，則可以劃分至0類或1類。對於0-1型變數，y=1的概率分佈公式定義如下：



y=0的概率分佈公式定義如下：



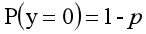
其離散型隨機變數期望值公式如下：



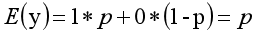
採用線性模型進行分析，其公式變換如下：



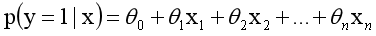
而實際應用中，概率p與因變數往往是非線性的，為了解決該類問題，我們引入了logit變換，使得logit(p)與自變數之
間存線上性相關的關係，邏輯迴歸模型定義如下：



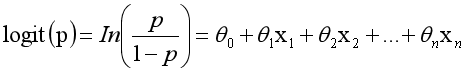
通過推導，概率p變換如下，這與Sigmoid函式相符，也體現了概率p與因變數之間的非線性關係。以0.5為界限，預測p大於0.5時，我們判斷此時y更可能為1，否則y為0。



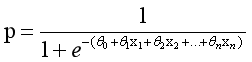
得到所需的Sigmoid函式後，接下來只需要和前面的線性迴歸一樣，擬合出該式中n個引數θ即可。test17_05.py為繪製Sigmoid曲線，輸出上圖所示。

import matplotlib.pyplot as plt
import numpy as np

def Sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))

x= np.arange(-10, 10, 0.1)
h = Sigmoid(x)            #Sigmoid函式
plt.plot(x, h)
plt.axvline(0.0, color='k')   #座標軸上加一條豎直的線（0位置）
plt.axhspan(0.0, 1.0, facecolor='1.0', alpha=1.0, ls='dotted')  
plt.axhline(y=0.5, ls='dotted', color='k') 
plt.yticks([0.0, 0.5, 1.0])  #y軸標度
plt.ylim(-0.1, 1.1)       #y軸範圍
plt.show()
由於篇幅有限，邏輯迴歸構造損失函式J函式，求解最小J函式及迴歸引數θ的方法就不在敘述，原理和前面小節一樣，請讀者下去深入研究。



二. LogisticRegression迴歸演算法

LogisticRegression迴歸模型在Sklearn.linear_model子類下，呼叫sklearn邏輯迴歸演算法步驟比較簡單，即：
    (1) 匯入模型。呼叫邏輯迴歸LogisticRegression()函式。
    (2) fit()訓練。呼叫fit(x,y)的方法來訓練模型，其中x為資料的屬性，y為所屬型別。
    (3) predict()預測。利用訓練得到的模型對資料集進行預測，返回預測結果。

程式碼如下：

from sklearn.linear_model import LogisticRegression  #匯入邏輯迴歸模型 
clf = LogisticRegression()
print clf
clf.fit(train_feature,label)
predict['label'] = clf.predict(predict_feature)
輸出結果如下：
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
          penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
          verbose=0, warm_start=False)
其中，引數penalty表示懲罰項（L1、L2值可選。L1向量中各元素絕對值的和，作用是產生少量的特徵，而其他特徵都是0，常用於特徵選擇；L2向量中各個元素平方之和再開根號，作用是選擇較多的特徵，使他們都趨近於0。）； C值的目標函式約束條件：s.t.||w||1<C，預設值是0，C值越小，則正則化強度越大。


三. 分析鳶尾花資料集

下面將結合Scikit-learn官網的邏輯迴歸模型分析鳶尾花示例，給大家進行詳細講解及擴充。由於該資料集分類標籤劃分為3類（0類、1類、2類），很好的適用於邏輯迴歸模型。

1. 鳶尾花資料集

在Sklearn機器學習包中，整合了各種各樣的資料集，包括前面的糖尿病資料集，這裡引入的是鳶尾花卉（Iris）資料集，它是很常用的一個資料集。鳶尾花有三個亞屬，分別是山鳶尾（Iris-setosa）、變色鳶尾（Iris-versicolor）和維吉尼亞鳶尾（Iris-virginica）。

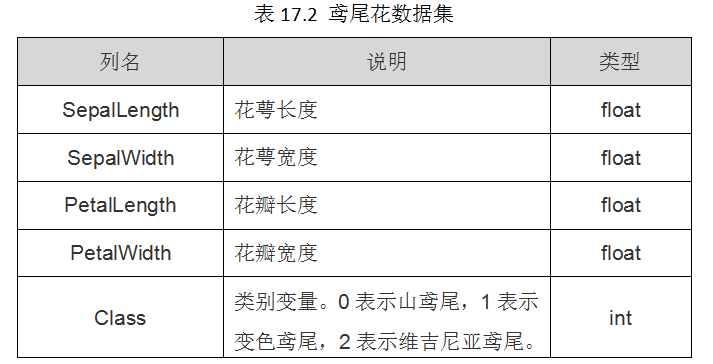
該資料集一共包含4個特徵變數，1個類別變數。共有150個樣本，iris是鳶尾植物，這裡儲存了其萼片和花瓣的長寬，共4個屬性，鳶尾植物分三類。如表17.2所示：


iris裡有兩個屬性iris.data，iris.target。data是一個矩陣，每一列代表了萼片或花瓣的長寬，一共4列，每一列代表某個被測量的鳶尾植物，一共取樣了150條記錄。
from sklearn.datasets import load_iris   #匯入資料集iris
iris = load_iris()  #載入資料集
print iris.data
輸出如下所示：
[[ 5.1  3.5  1.4  0.2]
 [ 4.9  3.   1.4  0.2]
 [ 4.7  3.2  1.3  0.2]
 [ 4.6  3.1  1.5  0.2]
 ....
 [ 6.7  3.   5.2  2.3]
 [ 6.3  2.5  5.   1.9]
 [ 6.5  3.   5.2  2. ]
 [ 6.2  3.4  5.4  2.3]
 [ 5.9  3.   5.1  1.8]]
target是一個陣列，儲存了data中每條記錄屬於哪一類鳶尾植物，所以陣列的長度是150，陣列元素的值因為共有3類鳶尾植物，所以不同值只有3個。種類為山鳶尾、雜色鳶尾、維吉尼亞鳶尾。
print iris.target          #輸出真實標籤
print len(iris.target)      #150個樣本 每個樣本4個特徵
print iris.data.shape  

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
150
(150L, 4L)
從輸出結果可以看到，類標共分為三類，前面50個類標位0，中間50個類標位1，後面為2。下面給詳細介紹使用決策樹進行對這個資料集進行測試的程式碼。

2. 散點圖繪製

下列程式碼主要是載入鳶尾花資料集，包括資料data和標籤target，然後獲取其中兩列資料或兩個特徵，核心程式碼為：X = [x[0] for x in DD]，獲取的值賦值給X變數，最後呼叫scatter()函式繪製散點圖。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris    #匯入資料集iris
  
#載入資料集  
iris = load_iris()  
print iris.data          #輸出資料集  
print iris.target         #輸出真實標籤  
#獲取花卉兩列資料集  
DD = iris.data  
X = [x[0] for x in DD]  
print X  
Y = [x[1] for x in DD]  
print Y  
  
#plt.scatter(X, Y, c=iris.target, marker='x')
plt.scatter(X[:50], Y[:50], color='red', marker='o', label='setosa') #前50個樣本
plt.scatter(X[50:100], Y[50:100], color='blue', marker='x', label='versicolor') #中間50個
plt.scatter(X[100:], Y[100:],color='green', marker='+', label='Virginica') #後50個樣本
plt.legend(loc=2) #左上角
plt.show()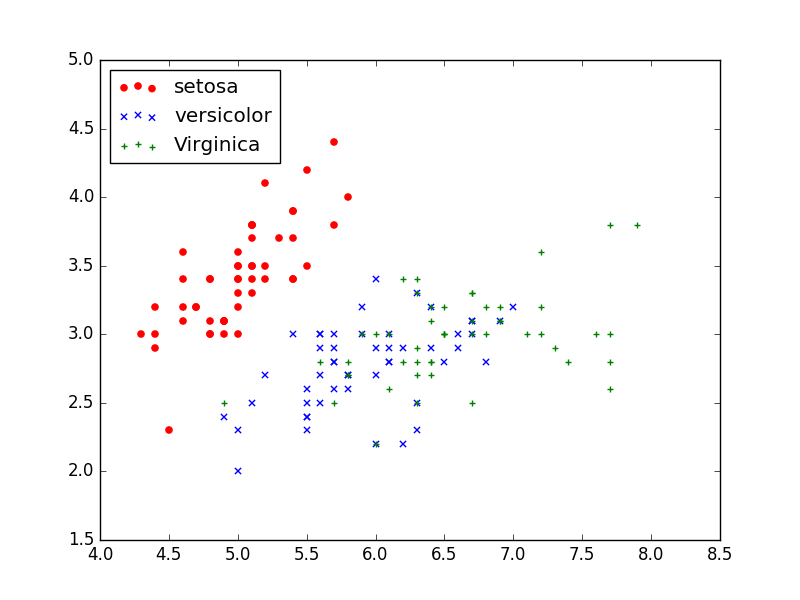
繪製散點圖如圖所示：


3. 邏輯迴歸分析

從圖中可以看出，資料集線性可分的，可以劃分為3類，分別對應三種型別的鳶尾花，下面採用邏輯迴歸對其進行分類預測。前面使用X=[x[0] for x in DD]獲取第一列資料，Y=[x[1] for x in DD]獲取第二列資料，這裡採用另一種方法，iris.data[:, :2]獲取其中兩列資料（兩個特徵），完整程式碼如下：

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris   
from sklearn.linear_model import LogisticRegression 

#載入資料集
iris = load_iris()         
X = X = iris.data[:, :2]   #獲取花卉兩列資料集
Y = iris.target           

#邏輯迴歸模型
lr = LogisticRegression(C=1e5)  
lr.fit(X,Y)

#meshgrid函式生成兩個網格矩陣
h = .02
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

#pcolormesh函式將xx,yy兩個網格矩陣和對應的預測結果Z繪製在圖片上
Z = lr.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(8,6))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)

#繪製散點圖
plt.scatter(X[:50,0], X[:50,1], color='red',marker='o', label='setosa')
plt.scatter(X[50:100,0], X[50:100,1], color='blue', marker='x', label='versicolor')
plt.scatter(X[100:,0], X[100:,1], color='green', marker='s', label='Virginica') 

plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.legend(loc=2) 
plt.show()
下面作者對匯入資料集後的程式碼進行詳細講解。

lr = LogisticRegression(C=1e5)  
lr.fit(X,Y)
初始化邏輯迴歸模型並進行訓練，C=1e5表示目標函式。

x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
獲取的鳶尾花兩列資料，對應為花萼長度和花萼寬度，每個點的座標就是(x,y)。 先取X二維陣列的第一列（長度）的最小值、最大值和步長h（設定為0.02）生成陣列，再取X二維陣列的第二列（寬度）的最小值、最大值和步長h生成陣列， 最後用meshgrid函式生成兩個網格矩陣xx和yy，如下所示：

[[ 3.8   3.82  3.84 ...,  8.36  8.38  8.4 ]
 [ 3.8   3.82  3.84 ...,  8.36  8.38  8.4 ]
 ..., 
 [ 3.8   3.82  3.84 ...,  8.36  8.38  8.4 ]
 [ 3.8   3.82  3.84 ...,  8.36  8.38  8.4 ]]
[[ 1.5   1.5   1.5  ...,  1.5   1.5   1.5 ]
 [ 1.52  1.52  1.52 ...,  1.52  1.52  1.52]
 ..., 
 [ 4.88  4.88  4.88 ...,  4.88  4.88  4.88]
 [ 4.9   4.9   4.9  ...,  4.9   4.9   4.9 ]]

Z = lr.predict(np.c_[xx.ravel(), yy.ravel()])
呼叫ravel()函式將xx和yy的兩個矩陣轉變成一維陣列，由於兩個矩陣大小相等，因此兩個一維陣列大小也相等。np.c_[xx.ravel(), yy.ravel()]是獲取矩陣，即：

xx.ravel() 
[ 3.8   3.82  3.84 ...,  8.36  8.38  8.4 ]
yy.ravel() 
[ 1.5  1.5  1.5 ...,  4.9  4.9  4.9]
np.c_[xx.ravel(), yy.ravel()]
[[ 3.8   1.5 ]
 [ 3.82  1.5 ]
 [ 3.84  1.5 ]
 ..., 
 [ 8.36  4.9 ]
 [ 8.38  4.9 ]
 [ 8.4   4.9 ]]

總結下：上述操作是把第一列花萼長度資料按h取等分作為行，並複製多行得到xx網格矩陣；再把第二列花萼寬度資料按h取等分，作為列，並複製多列得到yy網格矩陣；最後將xx和yy矩陣都變成兩個一維陣列，呼叫np.c_[]函式組合成一個二維陣列進行預測。
呼叫predict()函式進行預測，預測結果賦值給Z。即：

Z = logreg.predict(np.c_[xx.ravel(), yy.ravel()])
[1 1 1 ..., 2 2 2]
size: 39501

Z = Z.reshape(xx.shape)
呼叫reshape()函式修改形狀，將其Z轉換為兩個特徵（長度和寬度），則39501個資料轉換為171*231的矩陣。Z = Z.reshape(xx.shape)輸出如下：

[[1 1 1 ..., 2 2 2]
 [1 1 1 ..., 2 2 2]
 [0 1 1 ..., 2 2 2]
 ..., 
 [0 0 0 ..., 2 2 2]
 [0 0 0 ..., 2 2 2]
 [0 0 0 ..., 2 2 2]]

plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
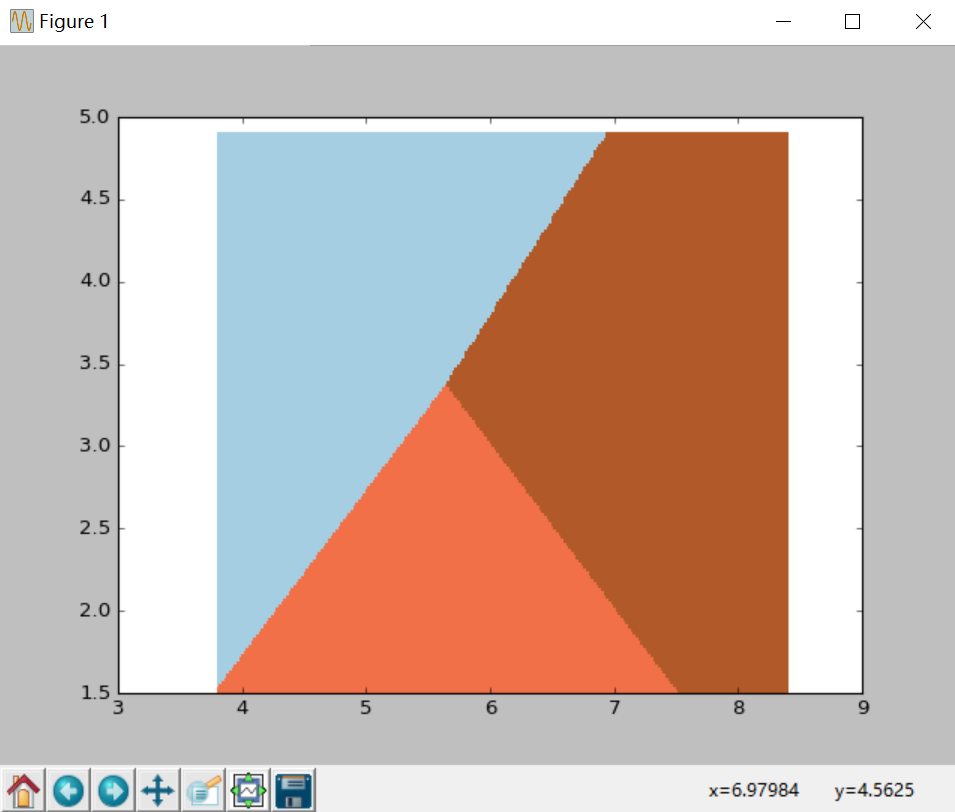
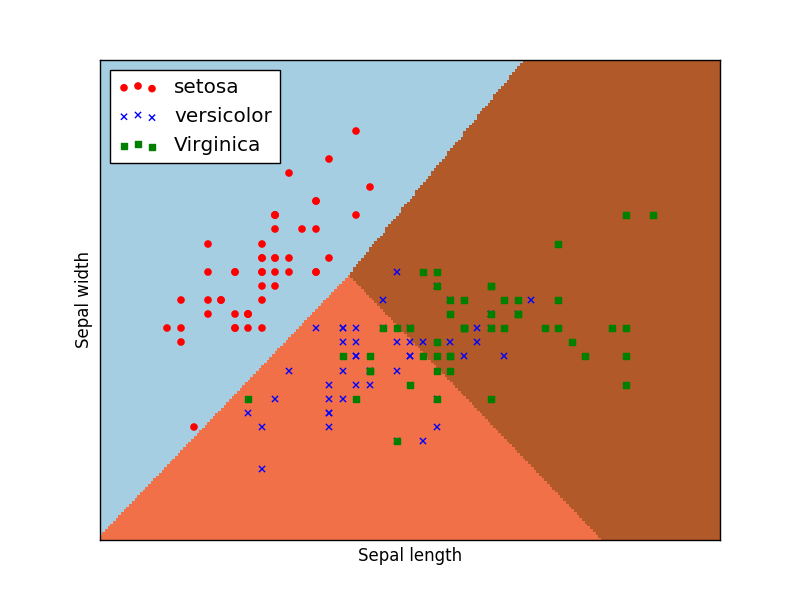
呼叫pcolormesh()函式將xx、yy兩個網格矩陣和對應的預測結果Z繪製在圖片上，可以發現輸出為三個顏色區塊，分佈表示分類的三類區域。cmap=plt.cm.Paired表示繪圖樣式選擇Paired主題。輸出的區域如下圖所示：



plt.scatter(X[:50,0], X[:50,1], color='red',marker='o', label='setosa')
呼叫scatter()繪製散點圖，第一個引數為第一列資料（長度），第二個引數為第二列資料（寬度），第三、四個引數為設定點的顏色為紅色，款式為圓圈，最後標記為setosa。

輸出如下圖所示，經過邏輯迴歸後劃分為三個區域，左上角部分為紅色的圓點，對應setosa鳶尾花；右上角部分為綠色方塊，對應virginica鳶尾花；中間下部分為藍色星形，對應versicolor鳶尾花。散點圖為各資料點真實的花型別，劃分的三個區域為資料點預測的花型別，預測的分類結果與訓練資料的真實結果結果基本一致，部分鳶尾花出現交叉。



迴歸演算法作為統計學中最重要的工具之一，它通過建立一個迴歸方程用來預測目標值，並求解這個迴歸方程的迴歸係數。本篇文章詳細講解了邏輯迴歸模型的原理知識，結合Sklearn機器學習庫的LogisticRegression演算法分析了鳶尾花分類情況。更多知識點希望讀者下來後進行擴充，也推薦大學從Sklearn開源知識官網學習最新的例項。
希望文章對你有所幫助，祝自己和娜老師教師節快樂~接著工作去了

(By:Eastmount 2017-09-10 中午12點  http://blog.csdn.net/eastmount/ )


相關文章