【python資料探勘課程】十四.Scipy呼叫curve_fit實現曲線擬合

        前面系列文章講過各種知識，包括繪製曲線、散點圖、冪分佈等，而如何在在散點圖一堆點中擬合一條直線，也變得非常重要。這篇文章主要講述呼叫Scipy擴充套件包的curve_fit函式實現曲線擬合，同時計算出擬合的函式、引數等。希望文章對你有所幫助，如果文章中存在錯誤或不足之處，還請海涵~

        前文推薦：
       【Python資料探勘課程】一.安裝Python及爬蟲入門介紹
       【Python資料探勘課程】二.Kmeans聚類資料分析及Anaconda介紹
       【Python資料探勘課程】三.Kmeans聚類程式碼實現、作業及優化
       【Python資料探勘課程】四.決策樹DTC資料分析及鳶尾資料集分析
       【Python資料探勘課程】五.線性迴歸知識及預測糖尿病例項
       【Python資料探勘課程】六.Numpy、Pandas和Matplotlib包基礎知識
       【Python資料探勘課程】七.PCA降維操作及subplot子圖繪製
       【Python資料探勘課程】八.關聯規則挖掘及Apriori實現購物推薦
       【Python資料探勘課程】九.迴歸模型LinearRegression簡單分析氧化物資料
       【python資料探勘課程】十.Pandas、Matplotlib、PCA繪圖實用程式碼補充
       【python資料探勘課程】十一.Pandas、Matplotlib結合SQL語句視覺化分析
       【python資料探勘課程】十二.Pandas、Matplotlib結合SQL語句對比圖分析
       【python資料探勘課程】十三.WordCloud詞雲配置過程及詞頻分析

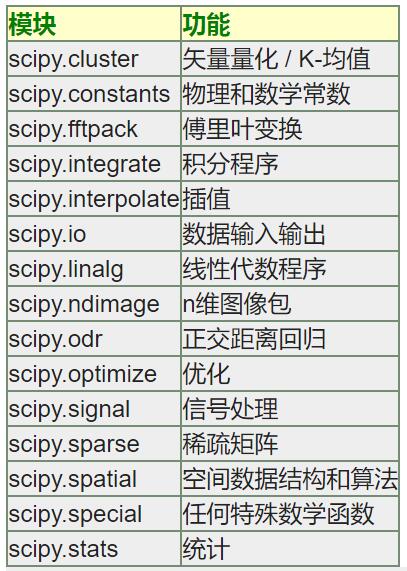
一. Scipy介紹

        SciPy (pronounced "Sigh Pie") 是一個開源的數學、科學和工程計算包。它是一款方便、易於使用、專為科學和工程設計的Python工具包，包括統計、優化、整合、線性代數模組、傅立葉變換、訊號和影象處理、常微分方程求解器等等。
        官方地址：https://www.scipy.org/

        Scipy常用的模組及功能如下圖所示：
        強烈推薦劉神的文章：Scipy高階科學計算 - 劉一痕

        Scipy優化和擬合採用的是optimize模組，該模組提供了函式最小值(標量或多維)、曲線擬合和尋找等式的根的有用演算法。

        官方介紹：scipy.optimize.curve_fit
        下面將從例項進行詳細介紹，包括：
        1.呼叫 numpy.polyfit() 函式實現一次二次多項式擬合；
        2.Pandas匯入資料後，呼叫Scipy實現次方擬合；
        3.實現np.exp()形式e的次方擬合；
        4.實現三個引數的形式擬合；
        5.最後通過冪率圖形分析介紹自己的一些想法和問題。

二. 曲線擬合

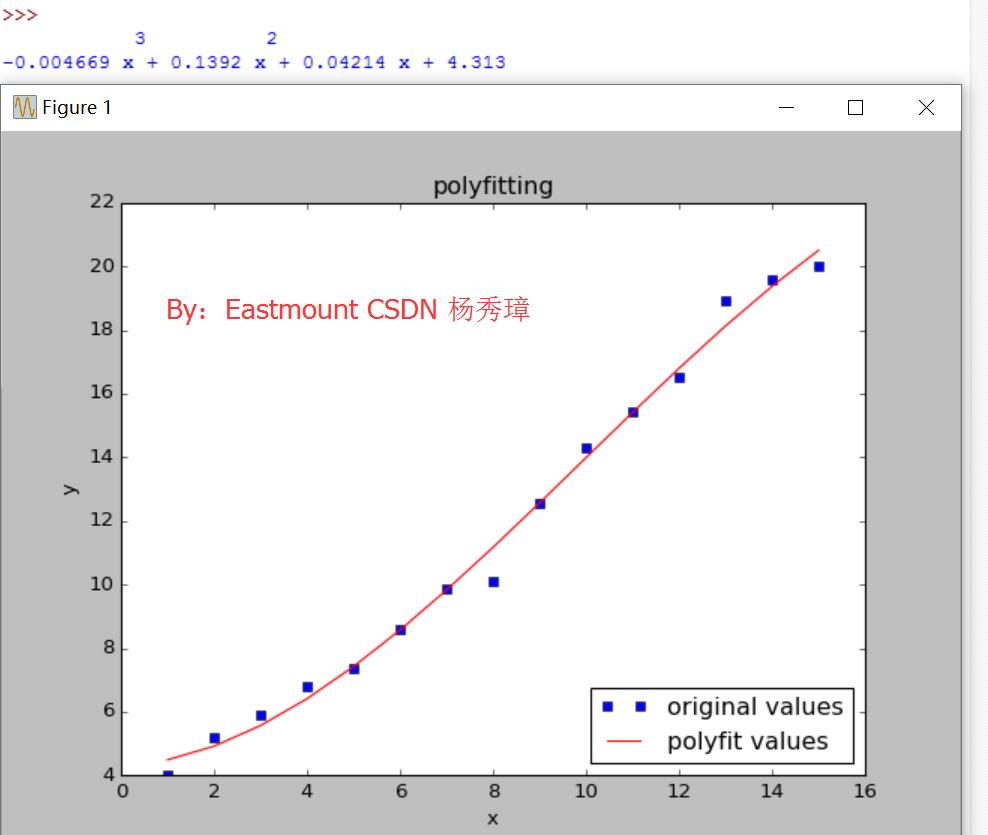
1.多項式擬合

        首先通過numpy.arange定義x、y座標，然後呼叫polyfit()函式進行3次多項式擬合，最後呼叫Matplotlib函式進行散點圖繪製(x,y)座標，並繪製預測的曲線。
        完整程式碼：

#encoding=utf-8  
import numpy as np
import matplotlib.pyplot as plt

#定義x、y散點座標
x = np.arange(1, 16, 1)
num = [4.00, 5.20, 5.900, 6.80, 7.34,
       8.57, 9.86, 10.12, 12.56, 14.32,
       15.42, 16.50, 18.92, 19.58, 20.00]
y = np.array(num)

#用3次多項式擬合
f1 = np.polyfit(x, y, 3)
p1 = np.poly1d(f1)
print(p1)

#也可使用yvals=np.polyval(f1, x)
yvals = p1(x)  #擬合y值

#繪圖
plot1 = plt.plot(x, y, 's',label='original values')
plot2 = plt.plot(x, yvals, 'r',label='polyfit values')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4) #指定legend的位置右下角
plt.title('polyfitting')
plt.show()
plt.savefig('test.png')

        輸出結果如下圖所示，包括藍色的正方形散點和紅色的擬合曲線。
        多項式函式為: y=-0.004669 x3 + 0.1392 x2 + 0.04214 x + 4.313

        補充：給出函式，可以用 Origin 進行繪圖的，也比較方便。

2.e的b/x次方擬合

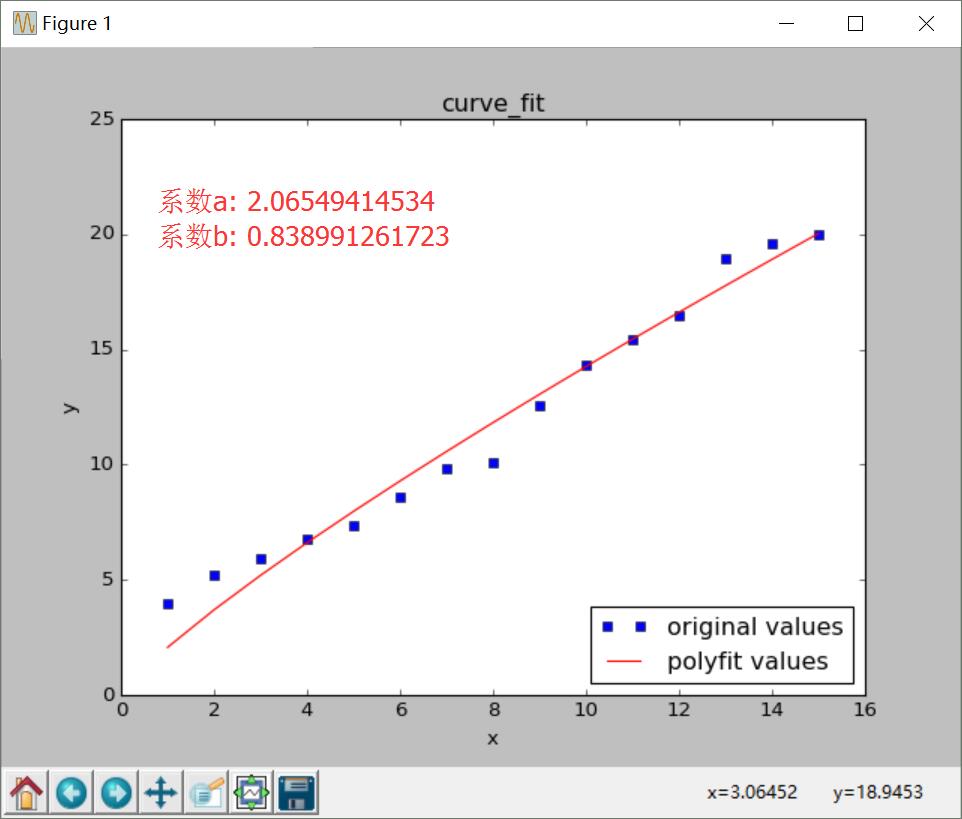
        下面採用Scipy的curve_fit()對上面的資料進行e的b/x次方擬合。資料集如下：

x = np.arange(1, 16, 1)
num = [4.00, 5.20, 5.900, 6.80, 7.34,
       8.57, 9.86, 10.12, 12.56, 14.32,
       15.42, 16.50, 18.92, 19.58, 20.00]
y = np.array(num)

        其中，x座標從1到15，y對應Num陣列，比如第一個點(1, 4.00)、最後一個點(15, 20.00)。
        然後呼叫curve_fit()函式，核心步驟：
        (1) 定義需要擬合的函式型別，如：
            def func(x, a, b):
                return a*np.exp(b/x)
        (2) 呼叫 popt, pcov = curve_fit(func, x, y) 函式進行擬合，並將擬合係數儲存在popt中，a=popt[0]、b=popt[1]進行呼叫；
        (3) 呼叫func(x, a, b)函式，其中x表示橫軸表，a、b表示對應的引數。
        完整程式碼如下：

#encoding=utf-8  
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

#自定義函式 e指數形式
def func(x, a, b):
    return a*np.exp(b/x)

#定義x、y散點座標
x = np.arange(1, 16, 1)
num = [4.00, 5.20, 5.900, 6.80, 7.34,
       8.57, 9.86, 10.12, 12.56, 14.32,
       15.42, 16.50, 18.92, 19.58, 20.00]
y = np.array(num)

#非線性最小二乘法擬合
popt, pcov = curve_fit(func, x, y)
#獲取popt裡面是擬合係數
a = popt[0] 
b = popt[1]
yvals = func(x,a,b) #擬合y值
print u'係數a:', a
print u'係數b:', b

#繪圖
plot1 = plt.plot(x, y, 's',label='original values')
plot2 = plt.plot(x, yvals, 'r',label='polyfit values')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4) #指定legend的位置右下角
plt.title('curve_fit')
plt.show()
plt.savefig('test2.png')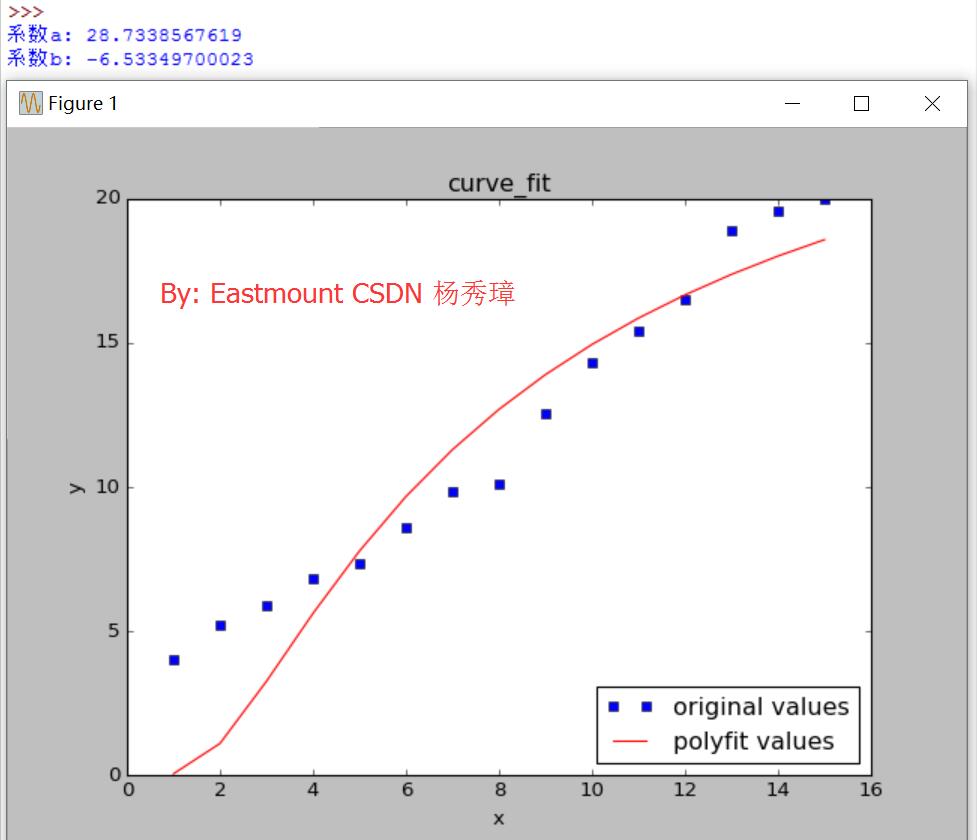

        繪製的圖形如下所示，擬合效果沒有多項式的好。

3.aX的b次方擬合

        第三種方法是通過Pandas匯入資料，因為通常資料都會儲存在csv、excel或資料庫中，所以這裡結合讀寫資料繪製a*x的b次方形式。
        假設本地存在一個data.csv檔案，資料集如下圖所示：

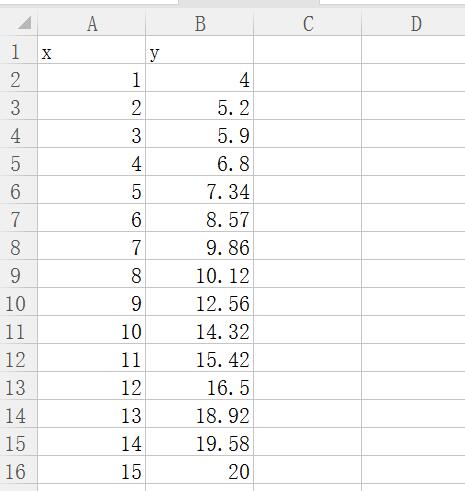
       然後呼叫Pandas擴充套件包讀取資料，並獲取x、y值顯示，這段程式碼如下：

#匯入資料及x、y散點座標
data = pd.read_csv("data.csv")
print data
print(data.shape)    
print(data.head(5)) #顯示前5行資料
x = data['x'] #獲取x列
y = data['y'] #獲取y列
print x
print y

        比如 print y 輸出結果：

0      4.00
1      5.20
2      5.90
3      6.80
4      7.34
5      8.57
6      9.86
7     10.12
8     12.56
9     14.32
10    15.42
11    16.50
12    18.92
13    19.58
14    20.00
Name: y, dtype: float64

        最後完整的擬合程式碼如下所示：

#encoding=utf-8  
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import pandas as pd  

#自定義函式 e指數形式
def func(x, a, b):
    return a*pow(x,b)

#匯入資料及x、y散點座標
data = pd.read_csv("data.csv")
print data
print(data.shape)    
print(data.head(5)) #顯示前5行資料
x = data['x']
y = data['y']
print x
print y

#非線性最小二乘法擬合
popt, pcov = curve_fit(func, x, y)
#獲取popt裡面是擬合係數
a = popt[0] 
b = popt[1]
yvals = func(x,a,b) #擬合y值
print u'係數a:', a
print u'係數b:', b

#繪圖
plot1 = plt.plot(x, y, 's',label='original values')
plot2 = plt.plot(x, yvals, 'r',label='polyfit values')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4) #指定legend的位置右下角
plt.title('curve_fit')
plt.savefig('test3.png')
plt.show()

        輸出結果如下圖所示：

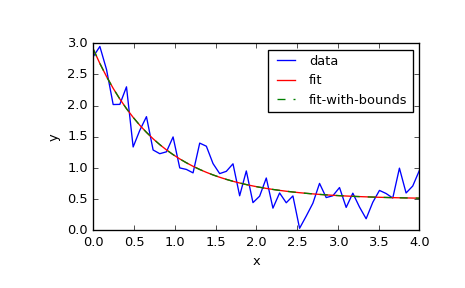
4.三個引數擬合

        最後介紹官方給出的例項，講述傳遞三個引數，通常為 a*e(b/x)+c形式。

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

def func(x, a, b, c):
    return a * np.exp(-b * x) + c

# define the data to be fit with some noise
xdata = np.linspace(0, 4, 50)
y = func(xdata, 2.5, 1.3, 0.5)
y_noise = 0.2 * np.random.normal(size=xdata.size)
ydata = y + y_noise
plt.plot(xdata, ydata, 'b-', label='data')

# Fit for the parameters a, b, c of the function `func`
popt, pcov = curve_fit(func, xdata, ydata)
plt.plot(xdata, func(xdata, *popt), 'r-', label='fit')

# Constrain the optimization to the region of ``0 < a < 3``, ``0 < b < 2``
# and ``0 < c < 1``:
popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 2., 1.]))
plt.plot(xdata, func(xdata, *popt), 'g--', label='fit-with-bounds')

plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

        輸出結果如下圖所示：

三. 冪律分佈擬合及疑問

        下面是我冪率分佈的實驗，因為涉及到保密，所以只提出幾個問題。
        圖1是多項式的擬合結果，基本符合圖形趨勢。
        圖2是冪指數擬合結果，冪指數為-1.18也符合人類的基本活動規律。

        問題：
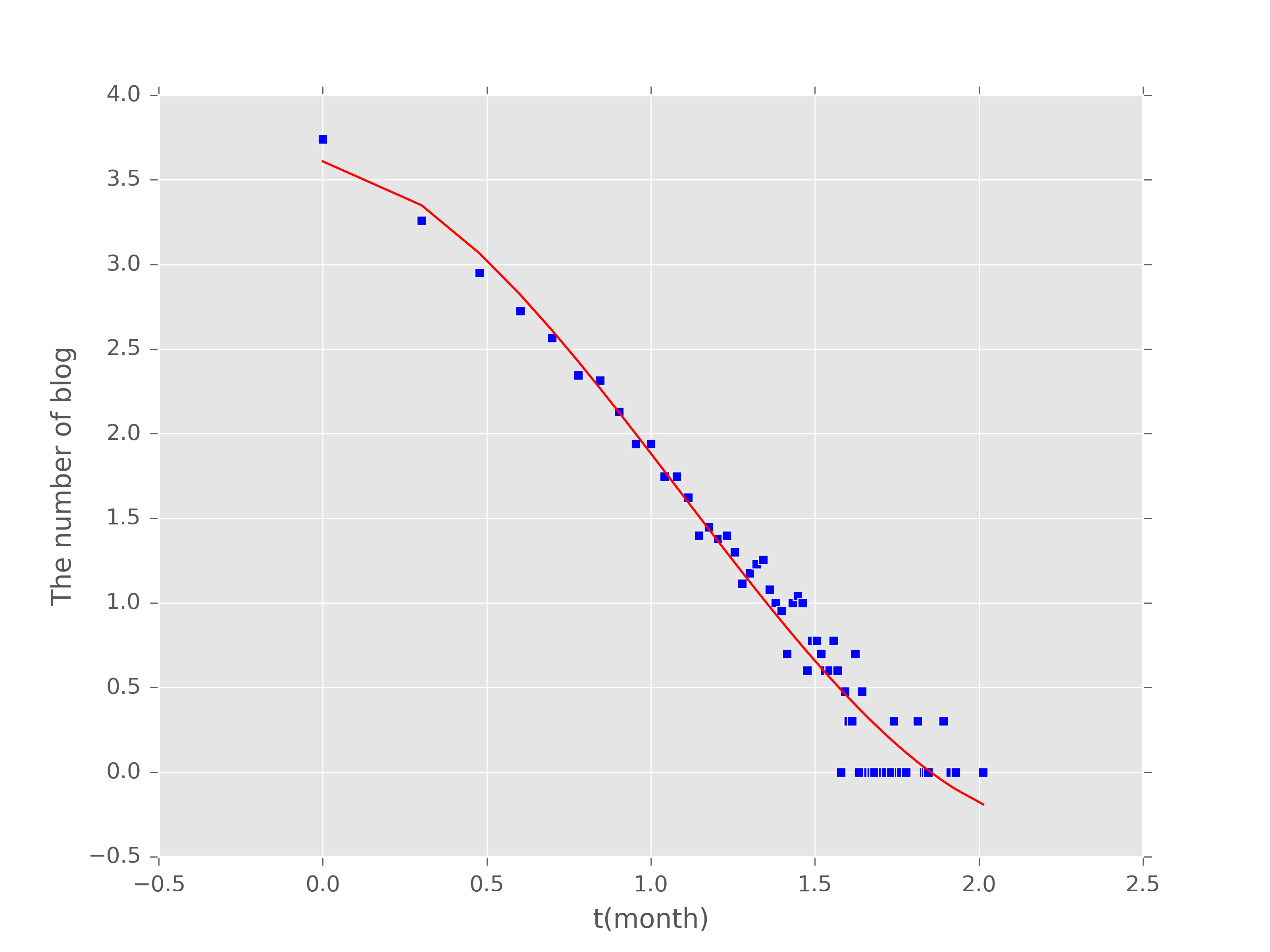
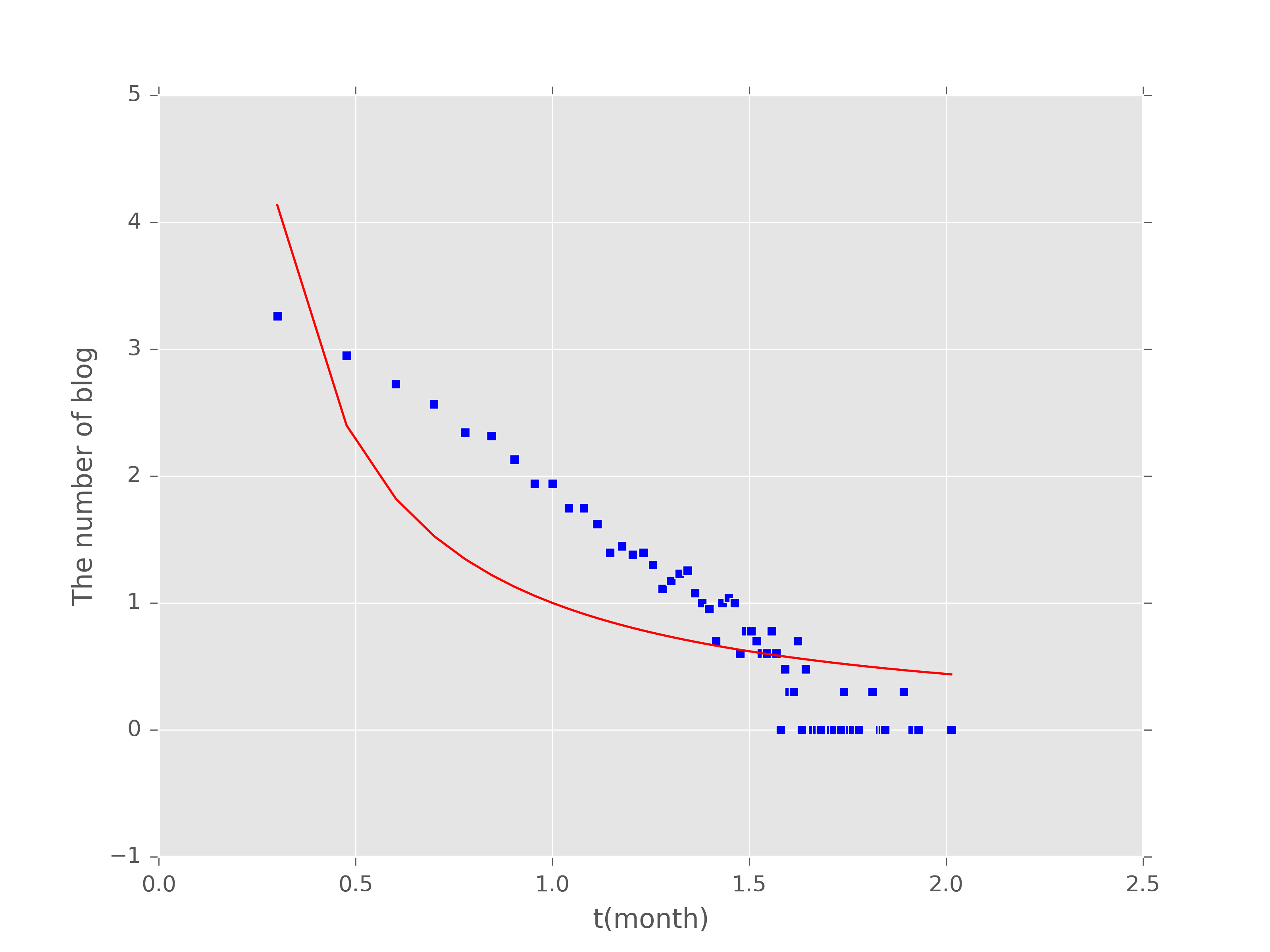
        1.為什麼冪律分佈擬合的圖形不太好，而指數卻很好；
        2.計算冪指數及擬合是否只對中間那部分效果好的進行擬合；
        3.e的b/x次方、多項方程、x的b次方哪個效果好？