【Python資料探勘課程】九.迴歸模型LinearRegression簡單分析氧化物資料

Eastmount發表於2017-03-05
Python模型
        這篇文章主要介紹三個知識點，也是我《資料探勘與分析》課程講課的內容。同時主要參考學生的課程提交作業內容進行講述，包括：
        1.迴歸模型及基礎知識；
        2.UCI資料集；
        3.迴歸模型簡單資料分析。

        前文推薦：
       【Python資料探勘課程】一.安裝Python及爬蟲入門介紹
       【Python資料探勘課程】二.Kmeans聚類資料分析及Anaconda介紹
       【Python資料探勘課程】三.Kmeans聚類程式碼實現、作業及優化
       【Python資料探勘課程】四.決策樹DTC資料分析及鳶尾資料集分析
       【Python資料探勘課程】五.線性迴歸知識及預測糖尿病例項
       【Python資料探勘課程】六.Numpy、Pandas和Matplotlib包基礎知識
       【Python資料探勘課程】七.PCA降維操作及subplot子圖繪製
       【Python資料探勘課程】八.關聯規則挖掘及Apriori實現購物推薦
      

        希望這篇文章對你有所幫助，尤其是剛剛接觸資料探勘以及大資料的同學，這些基礎知識真的非常重要。如果文章中存在不足或錯誤的地方，還請海涵~
        感謝ZJ學生提供的資料集與作品相關報告，學生確實還是學到了些東西。
        授課知識強推第五節課內容：五.線性迴歸知識及預測糖尿病例項


一. 演算法簡介-迴歸模型

1.初識迴歸

      “子女的身高趨向於高於父母的身高的平均值，但一般不會超過父母的身高。”
                                                                        -- 《遺傳的身高向平均數方向的迴歸》
        迴歸(Regression)這一概念最早由英國生物統計學家高爾頓和他的學生皮爾遜在研究父母親和子女的身高遺傳特性時提出。如今，我們做迴歸分析時所討論的“迴歸”和這種趨勢中效應已經沒有任何瓜葛了，它只是指源於高爾頓工作的那樣——用一個或多個自變數來預測因變數的數學方法。

        在一個迴歸模型中，我們需要關注或預測的變數叫做因變數（響應變數或結果變數），我們選取的用來解釋因變數變化的變數叫做自變數（解釋變數或預測變數）。



        迴歸是統計學中最有力的工具之一。機器學習監督學習演算法分為分類演算法和迴歸演算法兩種，其實就是根據類別標籤分佈型別為離散型、連續性而定義的。
        分類演算法用於離散型分佈預測，如KNN、決策樹、樸素貝葉斯、adaboost、SVM、Logistic迴歸都是分類演算法；迴歸演算法用於連續型分佈預測，針對的是數值型的樣本，使用迴歸，可以在給定輸入的時候預測出一個數值，這是對分類方法的提升，因為這樣可以預測連續型資料而不僅僅是離散的類別標籤。

        迴歸的目的就是建立一個迴歸方程用來預測目標值，迴歸的求解就是求這個迴歸方程的迴歸係數。預測的方法即迴歸係數乘以輸入值再全部相加就得到了預測值。


        迴歸最簡單的定義：給出一個點集D，用一個函式去擬合這個點集，並且使得點集與擬合函式間的誤差最小，如果這個函式曲線是一條直線，那就被稱為線性迴歸，如果曲線是一條二次曲線，就被稱為二次迴歸。

2.線性迴歸

         假定預測值與樣本特徵間的函式關係是線性的，迴歸分析的任務，就在於根據樣本X和Y的觀察值，去估計函式h，尋求變數之間近似的函式關係。定義：

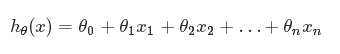
        其中，n = 特徵數目；xj = 每個訓練樣本第j個特徵的值，可以認為是特徵向量中的第j個值。
為了方便，記x0= 1，則多變數線性迴歸可以記為：
        其中，θ、x都表示(n+1，1)維列向量。

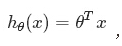
        注意：多元和多次是兩個不同的概念，“多元”指方程有多個引數，“多次”指的是方程中引數的最高次冪。多元線性方程是假設預測值y與樣本所有特徵值符合一個多元一次線性方程。


3.求解線性迴歸

        迴歸常常指線性迴歸，迴歸的求解就是多元線性迴歸方程的求解。假設有連續型值標籤(標籤值分佈為Y)的樣本，有X={x1,x2,...,xn}個特徵，迴歸就是求解迴歸係數θ=θ0, θ1,…,θn。那麼，手裡有一些X和對應的Y,怎樣才能找到θ呢？

         在迴歸方程裡，求得特徵對應的最佳迴歸係數的方法是最小化誤差的平方和。這裡的誤差是指預測y值和真實y值之間的差值，使用該誤差的簡單累加將使得正差值和負差值相互抵消，所以採用平方誤差（最小二乘法）。平方誤差可以寫做：


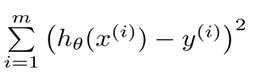
        在數學上，求解過程就轉化為求一組θ值使求上式取到最小值，那麼求解方法有梯度下降法、Normal Equation等等。

        梯度下降有如下特點：需要預先選定步長a、需要多次迭代、特徵值需要Scaling（統一到同一個尺度範圍）。因此比較複雜，還有一種不需要迭代的求解方式——Normal Equation，簡單、方便、不需要Feature Scaling。Normal Equation方法中需要計算X的轉置與逆矩陣，計算量很大，因此特徵個數多時計算會很慢，只適用於特徵個數小於100000時使用；當特徵數量大於100000時使用梯度法。

        另外，當X不可逆時就有嶺迴歸演算法的用武之地了。


        3.1 梯度下降法（Gradient Descent）

        根據平方誤差，定義該線性迴歸模型的損耗函式（Cost Function）為：   

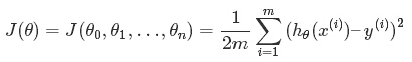
        線性迴歸的損耗函式的值與迴歸係數θ的關係是碗狀的，只有一個最小點。線性迴歸的求解過程如同Logistic迴歸，區別在於學習模型函式hθ(x)不同。

        3.2 普通最小二乘法（Normal Equation）
        Normal Equation演算法也叫做普通最小二乘法（ordinary least squares），其特點是：給定輸人矩陣X，如果X T X的逆存在並可以求得的話，就可以直接採用該方法求解。其求解理論也十分簡單：既然是是求最小誤差平方和，另其導數為0即可得出迴歸係數。

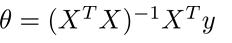
        矩陣X為（m，n+1）矩陣（m表示樣本數、n表示一個樣本的特徵數），y為（m，1）列向量。 上述公式中包含XTX, 也就是需要對矩陣求逆，因此這個方程只在逆矩陣存在的時候適用。

4.迴歸模型效能度量

         資料集上計算出的迴歸方程並不一定意味著它是最佳的，可以便用預測值yHat和原始值y的相關性來度量回歸方程的好壞。相關性取值範圍0~1，值越高說明迴歸模型效能越好。
         線性迴歸是假設值標籤與特徵值之間的關係是線性的，但有些時候資料間的關係可能會更加複雜，使用線性的模型就難以擬合，就需要引入多項式曲線迴歸（多元多次擬合）或者其他迴歸模型，如迴歸樹。

        注意：
        多元迴歸存在多重共線性，自相關性和異方差性。線性迴歸對異常值非常敏感。它會嚴重影響迴歸線，最終影響預測值。多重共線性會增加係數估計值的方差，使得在模型輕微變化下，估計非常敏感，結果就是係數估計值不穩定。


二. 資料集介紹

        在資料分析中資料集是最重要的資訊，推薦資料集UCI：
        http://archive.ics.uci.edu/ml/machine-learning-databases/
        該資料集包括6種型別的玻璃，各個特徵是定義它們的氧化物含量（即鈉，鐵，鉀等）。Mg：鎂 Ai：鋁 Si：矽 K：鉀 Ca：鈣 Ba：鋇  Fe：鐵  Type of glass：級屬性。
        資料集位glass.csv檔案，如下圖所示：



        詳細內容如下：

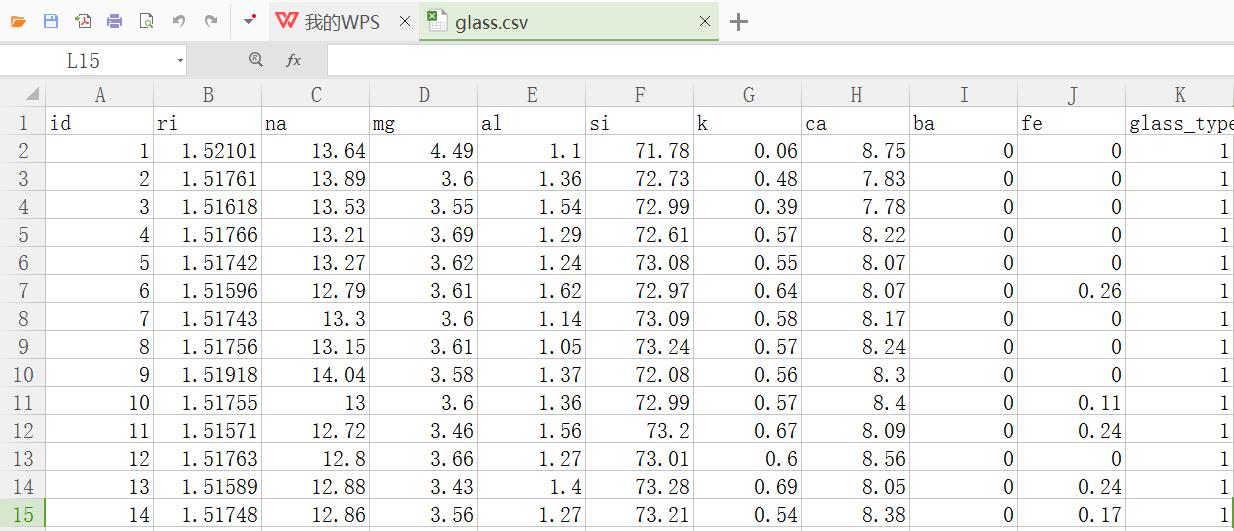
id	ri	na	mg	al	si	k	ca	ba	fe	glass_type
1	1.52101	13.64	4.49	1.1	71.78	0.06	8.75	0	0	1
2	1.51761	13.89	3.6	1.36	72.73	0.48	7.83	0	0	1
3	1.51618	13.53	3.55	1.54	72.99	0.39	7.78	0	0	1
4	1.51766	13.21	3.69	1.29	72.61	0.57	8.22	0	0	1
5	1.51742	13.27	3.62	1.24	73.08	0.55	8.07	0	0	1
6	1.51596	12.79	3.61	1.62	72.97	0.64	8.07	0	0.26	1
7	1.51743	13.3	3.6	1.14	73.09	0.58	8.17	0	0	1
8	1.51756	13.15	3.61	1.05	73.24	0.57	8.24	0	0	1
9	1.51918	14.04	3.58	1.37	72.08	0.56	8.3	0	0	1
10	1.51755	13	3.6	1.36	72.99	0.57	8.4	0	0.11	1
11	1.51571	12.72	3.46	1.56	73.2	0.67	8.09	0	0.24	1
12	1.51763	12.8	3.66	1.27	73.01	0.6	8.56	0	0	1
13	1.51589	12.88	3.43	1.4	73.28	0.69	8.05	0	0.24	1
14	1.51748	12.86	3.56	1.27	73.21	0.54	8.38	0	0.17	1
15	1.51763	12.61	3.59	1.31	73.29	0.58	8.5	0	0	1
16	1.51761	12.81	3.54	1.23	73.24	0.58	8.39	0	0	1
17	1.51784	12.68	3.67	1.16	73.11	0.61	8.7	0	0	1
18	1.52196	14.36	3.85	0.89	71.36	0.15	9.15	0	0	1
19	1.51911	13.9	3.73	1.18	72.12	0.06	8.89	0	0	1
20	1.51735	13.02	3.54	1.69	72.73	0.54	8.44	0	0.07	1
21	1.5175	12.82	3.55	1.49	72.75	0.54	8.52	0	0.19	1
22	1.51966	14.77	3.75	0.29	72.02	0.03	9	0	0	1
23	1.51736	12.78	3.62	1.29	72.79	0.59	8.7	0	0	1
24	1.51751	12.81	3.57	1.35	73.02	0.62	8.59	0	0	1
25	1.5172	13.38	3.5	1.15	72.85	0.5	8.43	0	0	1
26	1.51764	12.98	3.54	1.21	73	0.65	8.53	0	0	1
27	1.51793	13.21	3.48	1.41	72.64	0.59	8.43	0	0	1
28	1.51721	12.87	3.48	1.33	73.04	0.56	8.43	0	0	1
29	1.51768	12.56	3.52	1.43	73.15	0.57	8.54	0	0	1
30	1.51784	13.08	3.49	1.28	72.86	0.6	8.49	0	0	1
31	1.51768	12.65	3.56	1.3	73.08	0.61	8.69	0	0.14	1
32	1.51747	12.84	3.5	1.14	73.27	0.56	8.55	0	0	1
33	1.51775	12.85	3.48	1.23	72.97	0.61	8.56	0.09	0.22	1
34	1.51753	12.57	3.47	1.38	73.39	0.6	8.55	0	0.06	1
35	1.51783	12.69	3.54	1.34	72.95	0.57	8.75	0	0	1
36	1.51567	13.29	3.45	1.21	72.74	0.56	8.57	0	0	1
37	1.51909	13.89	3.53	1.32	71.81	0.51	8.78	0.11	0	1
38	1.51797	12.74	3.48	1.35	72.96	0.64	8.68	0	0	1
39	1.52213	14.21	3.82	0.47	71.77	0.11	9.57	0	0	1
40	1.52213	14.21	3.82	0.47	71.77	0.11	9.57	0	0	1
41	1.51793	12.79	3.5	1.12	73.03	0.64	8.77	0	0	1
42	1.51755	12.71	3.42	1.2	73.2	0.59	8.64	0	0	1
43	1.51779	13.21	3.39	1.33	72.76	0.59	8.59	0	0	1
44	1.5221	13.73	3.84	0.72	71.76	0.17	9.74	0	0	1
45	1.51786	12.73	3.43	1.19	72.95	0.62	8.76	0	0.3	1
46	1.519	13.49	3.48	1.35	71.95	0.55	9	0	0	1
47	1.51869	13.19	3.37	1.18	72.72	0.57	8.83	0	0.16	1
48	1.52667	13.99	3.7	0.71	71.57	0.02	9.82	0	0.1	1
49	1.52223	13.21	3.77	0.79	71.99	0.13	10.02	0	0	1
50	1.51898	13.58	3.35	1.23	72.08	0.59	8.91	0	0	1
51	1.5232	13.72	3.72	0.51	71.75	0.09	10.06	0	0.16	1
52	1.51926	13.2	3.33	1.28	72.36	0.6	9.14	0	0.11	1
53	1.51808	13.43	2.87	1.19	72.84	0.55	9.03	0	0	1
54	1.51837	13.14	2.84	1.28	72.85	0.55	9.07	0	0	1
55	1.51778	13.21	2.81	1.29	72.98	0.51	9.02	0	0.09	1
56	1.51769	12.45	2.71	1.29	73.7	0.56	9.06	0	0.24	1
57	1.51215	12.99	3.47	1.12	72.98	0.62	8.35	0	0.31	1
58	1.51824	12.87	3.48	1.29	72.95	0.6	8.43	0	0	1
59	1.51754	13.48	3.74	1.17	72.99	0.59	8.03	0	0	1
60	1.51754	13.39	3.66	1.19	72.79	0.57	8.27	0	0.11	1
61	1.51905	13.6	3.62	1.11	72.64	0.14	8.76	0	0	1
62	1.51977	13.81	3.58	1.32	71.72	0.12	8.67	0.69	0	1
63	1.52172	13.51	3.86	0.88	71.79	0.23	9.54	0	0.11	1
64	1.52227	14.17	3.81	0.78	71.35	0	9.69	0	0	1
65	1.52172	13.48	3.74	0.9	72.01	0.18	9.61	0	0.07	1
66	1.52099	13.69	3.59	1.12	71.96	0.09	9.4	0	0	1
67	1.52152	13.05	3.65	0.87	72.22	0.19	9.85	0	0.17	1
68	1.52152	13.05	3.65	0.87	72.32	0.19	9.85	0	0.17	1
69	1.52152	13.12	3.58	0.9	72.2	0.23	9.82	0	0.16	1
70	1.523	13.31	3.58	0.82	71.99	0.12	10.17	0	0.03	1
71	1.51574	14.86	3.67	1.74	71.87	0.16	7.36	0	0.12	2
72	1.51848	13.64	3.87	1.27	71.96	0.54	8.32	0	0.32	2
73	1.51593	13.09	3.59	1.52	73.1	0.67	7.83	0	0	2
74	1.51631	13.34	3.57	1.57	72.87	0.61	7.89	0	0	2
75	1.51596	13.02	3.56	1.54	73.11	0.72	7.9	0	0	2
76	1.5159	13.02	3.58	1.51	73.12	0.69	7.96	0	0	2
77	1.51645	13.44	3.61	1.54	72.39	0.66	8.03	0	0	2
78	1.51627	13	3.58	1.54	72.83	0.61	8.04	0	0	2
79	1.51613	13.92	3.52	1.25	72.88	0.37	7.94	0	0.14	2
80	1.5159	12.82	3.52	1.9	72.86	0.69	7.97	0	0	2
81	1.51592	12.86	3.52	2.12	72.66	0.69	7.97	0	0	2
82	1.51593	13.25	3.45	1.43	73.17	0.61	7.86	0	0	2
83	1.51646	13.41	3.55	1.25	72.81	0.68	8.1	0	0	2
84	1.51594	13.09	3.52	1.55	72.87	0.68	8.05	0	0.09	2
85	1.51409	14.25	3.09	2.08	72.28	1.1	7.08	0	0	2
86	1.51625	13.36	3.58	1.49	72.72	0.45	8.21	0	0	2
87	1.51569	13.24	3.49	1.47	73.25	0.38	8.03	0	0	2
88	1.51645	13.4	3.49	1.52	72.65	0.67	8.08	0	0.1	2
89	1.51618	13.01	3.5	1.48	72.89	0.6	8.12	0	0	2
90	1.5164	12.55	3.48	1.87	73.23	0.63	8.08	0	0.09	2
91	1.51841	12.93	3.74	1.11	72.28	0.64	8.96	0	0.22	2
92	1.51605	12.9	3.44	1.45	73.06	0.44	8.27	0	0	2
93	1.51588	13.12	3.41	1.58	73.26	0.07	8.39	0	0.19	2
94	1.5159	13.24	3.34	1.47	73.1	0.39	8.22	0	0	2
95	1.51629	12.71	3.33	1.49	73.28	0.67	8.24	0	0	2
96	1.5186	13.36	3.43	1.43	72.26	0.51	8.6	0	0	2
97	1.51841	13.02	3.62	1.06	72.34	0.64	9.13	0	0.15	2
98	1.51743	12.2	3.25	1.16	73.55	0.62	8.9	0	0.24	2
99	1.51689	12.67	2.88	1.71	73.21	0.73	8.54	0	0	2
100	1.51811	12.96	2.96	1.43	72.92	0.6	8.79	0.14	0	2
101	1.51655	12.75	2.85	1.44	73.27	0.57	8.79	0.11	0.22	2
102	1.5173	12.35	2.72	1.63	72.87	0.7	9.23	0	0	2
103	1.5182	12.62	2.76	0.83	73.81	0.35	9.42	0	0.2	2
104	1.52725	13.8	3.15	0.66	70.57	0.08	11.64	0	0	2
105	1.5241	13.83	2.9	1.17	71.15	0.08	10.79	0	0	2
106	1.52475	11.45	0	1.88	72.19	0.81	13.24	0	0.34	2
107	1.53125	10.73	0	2.1	69.81	0.58	13.3	3.15	0.28	2
108	1.53393	12.3	0	1	70.16	0.12	16.19	0	0.24	2
109	1.52222	14.43	0	1	72.67	0.1	11.52	0	0.08	2
110	1.51818	13.72	0	0.56	74.45	0	10.99	0	0	2
111	1.52664	11.23	0	0.77	73.21	0	14.68	0	0	2
112	1.52739	11.02	0	0.75	73.08	0	14.96	0	0	2
113	1.52777	12.64	0	0.67	72.02	0.06	14.4	0	0	2
114	1.51892	13.46	3.83	1.26	72.55	0.57	8.21	0	0.14	2
115	1.51847	13.1	3.97	1.19	72.44	0.6	8.43	0	0	2
116	1.51846	13.41	3.89	1.33	72.38	0.51	8.28	0	0	2
117	1.51829	13.24	3.9	1.41	72.33	0.55	8.31	0	0.1	2
118	1.51708	13.72	3.68	1.81	72.06	0.64	7.88	0	0	2
119	1.51673	13.3	3.64	1.53	72.53	0.65	8.03	0	0.29	2
120	1.51652	13.56	3.57	1.47	72.45	0.64	7.96	0	0	2
121	1.51844	13.25	3.76	1.32	72.4	0.58	8.42	0	0	2
122	1.51663	12.93	3.54	1.62	72.96	0.64	8.03	0	0.21	2
123	1.51687	13.23	3.54	1.48	72.84	0.56	8.1	0	0	2
124	1.51707	13.48	3.48	1.71	72.52	0.62	7.99	0	0	2
125	1.52177	13.2	3.68	1.15	72.75	0.54	8.52	0	0	2
126	1.51872	12.93	3.66	1.56	72.51	0.58	8.55	0	0.12	2
127	1.51667	12.94	3.61	1.26	72.75	0.56	8.6	0	0	2
128	1.52081	13.78	2.28	1.43	71.99	0.49	9.85	0	0.17	2
129	1.52068	13.55	2.09	1.67	72.18	0.53	9.57	0.27	0.17	2
130	1.5202	13.98	1.35	1.63	71.76	0.39	10.56	0	0.18	2
131	1.52177	13.75	1.01	1.36	72.19	0.33	11.14	0	0	2
132	1.52614	13.7	0	1.36	71.24	0.19	13.44	0	0.1	2
133	1.51813	13.43	3.98	1.18	72.49	0.58	8.15	0	0	2
134	1.518	13.71	3.93	1.54	71.81	0.54	8.21	0	0.15	2
135	1.51811	13.33	3.85	1.25	72.78	0.52	8.12	0	0	2
136	1.51789	13.19	3.9	1.3	72.33	0.55	8.44	0	0.28	2
137	1.51806	13	3.8	1.08	73.07	0.56	8.38	0	0.12	2
138	1.51711	12.89	3.62	1.57	72.96	0.61	8.11	0	0	2
139	1.51674	12.79	3.52	1.54	73.36	0.66	7.9	0	0	2
140	1.51674	12.87	3.56	1.64	73.14	0.65	7.99	0	0	2
141	1.5169	13.33	3.54	1.61	72.54	0.68	8.11	0	0	2
142	1.51851	13.2	3.63	1.07	72.83	0.57	8.41	0.09	0.17	2
143	1.51662	12.85	3.51	1.44	73.01	0.68	8.23	0.06	0.25	2
144	1.51709	13	3.47	1.79	72.72	0.66	8.18	0	0	2
145	1.5166	12.99	3.18	1.23	72.97	0.58	8.81	0	0.24	2
146	1.51839	12.85	3.67	1.24	72.57	0.62	8.68	0	0.35	2
147	1.51769	13.65	3.66	1.11	72.77	0.11	8.6	0	0	3
148	1.5161	13.33	3.53	1.34	72.67	0.56	8.33	0	0	3
149	1.5167	13.24	3.57	1.38	72.7	0.56	8.44	0	0.1	3
150	1.51643	12.16	3.52	1.35	72.89	0.57	8.53	0	0	3
151	1.51665	13.14	3.45	1.76	72.48	0.6	8.38	0	0.17	3
152	1.52127	14.32	3.9	0.83	71.5	0	9.49	0	0	3
153	1.51779	13.64	3.65	0.65	73	0.06	8.93	0	0	3
154	1.5161	13.42	3.4	1.22	72.69	0.59	8.32	0	0	3
155	1.51694	12.86	3.58	1.31	72.61	0.61	8.79	0	0	3
156	1.51646	13.04	3.4	1.26	73.01	0.52	8.58	0	0	3
157	1.51655	13.41	3.39	1.28	72.64	0.52	8.65	0	0	3
158	1.52121	14.03	3.76	0.58	71.79	0.11	9.65	0	0	3
159	1.51776	13.53	3.41	1.52	72.04	0.58	8.79	0	0	3
160	1.51796	13.5	3.36	1.63	71.94	0.57	8.81	0	0.09	3
161	1.51832	13.33	3.34	1.54	72.14	0.56	8.99	0	0	3
162	1.51934	13.64	3.54	0.75	72.65	0.16	8.89	0.15	0.24	3
163	1.52211	14.19	3.78	0.91	71.36	0.23	9.14	0	0.37	3
164	1.51514	14.01	2.68	3.5	69.89	1.68	5.87	2.2	0	5
165	1.51915	12.73	1.85	1.86	72.69	0.6	10.09	0	0	5
166	1.52171	11.56	1.88	1.56	72.86	0.47	11.41	0	0	5
167	1.52151	11.03	1.71	1.56	73.44	0.58	11.62	0	0	5
168	1.51969	12.64	0	1.65	73.75	0.38	11.53	0	0	5
169	1.51666	12.86	0	1.83	73.88	0.97	10.17	0	0	5
170	1.51994	13.27	0	1.76	73.03	0.47	11.32	0	0	5
171	1.52369	13.44	0	1.58	72.22	0.32	12.24	0	0	5
172	1.51316	13.02	0	3.04	70.48	6.21	6.96	0	0	5
173	1.51321	13	0	3.02	70.7	6.21	6.93	0	0	5
174	1.52043	13.38	0	1.4	72.25	0.33	12.5	0	0	5
175	1.52058	12.85	1.61	2.17	72.18	0.76	9.7	0.24	0.51	5
176	1.52119	12.97	0.33	1.51	73.39	0.13	11.27	0	0.28	5
177	1.51905	14	2.39	1.56	72.37	0	9.57	0	0	6
178	1.51937	13.79	2.41	1.19	72.76	0	9.77	0	0	6
179	1.51829	14.46	2.24	1.62	72.38	0	9.26	0	0	6
180	1.51852	14.09	2.19	1.66	72.67	0	9.32	0	0	6
181	1.51299	14.4	1.74	1.54	74.55	0	7.59	0	0	6
182	1.51888	14.99	0.78	1.74	72.5	0	9.95	0	0	6
183	1.51916	14.15	0	2.09	72.74	0	10.88	0	0	6
184	1.51969	14.56	0	0.56	73.48	0	11.22	0	0	6
185	1.51115	17.38	0	0.34	75.41	0	6.65	0	0	6
186	1.51131	13.69	3.2	1.81	72.81	1.76	5.43	1.19	0	7
187	1.51838	14.32	3.26	2.22	71.25	1.46	5.79	1.63	0	7
188	1.52315	13.44	3.34	1.23	72.38	0.6	8.83	0	0	7
189	1.52247	14.86	2.2	2.06	70.26	0.76	9.76	0	0	7
190	1.52365	15.79	1.83	1.31	70.43	0.31	8.61	1.68	0	7
191	1.51613	13.88	1.78	1.79	73.1	0	8.67	0.76	0	7
192	1.51602	14.85	0	2.38	73.28	0	8.76	0.64	0.09	7
193	1.51623	14.2	0	2.79	73.46	0.04	9.04	0.4	0.09	7
194	1.51719	14.75	0	2	73.02	0	8.53	1.59	0.08	7
195	1.51683	14.56	0	1.98	73.29	0	8.52	1.57	0.07	7
196	1.51545	14.14	0	2.68	73.39	0.08	9.07	0.61	0.05	7
197	1.51556	13.87	0	2.54	73.23	0.14	9.41	0.81	0.01	7
198	1.51727	14.7	0	2.34	73.28	0	8.95	0.66	0	7
199	1.51531	14.38	0	2.66	73.1	0.04	9.08	0.64	0	7
200	1.51609	15.01	0	2.51	73.05	0.05	8.83	0.53	0	7
201	1.51508	15.15	0	2.25	73.5	0	8.34	0.63	0	7
202	1.51653	11.95	0	1.19	75.18	2.7	8.93	0	0	7
203	1.51514	14.85	0	2.42	73.72	0	8.39	0.56	0	7
204	1.51658	14.8	0	1.99	73.11	0	8.28	1.71	0	7
205	1.51617	14.95	0	2.27	73.3	0	8.71	0.67	0	7
206	1.51732	14.95	0	1.8	72.99	0	8.61	1.55	0	7
207	1.51645	14.94	0	1.87	73.11	0	8.67	1.38	0	7
208	1.51831	14.39	0	1.82	72.86	1.41	6.47	2.88	0	7
209	1.5164	14.37	0	2.74	72.85	0	9.45	0.54	0	7
210	1.51623	14.14	0	2.88	72.61	0.08	9.18	1.06	0	7
211	1.51685	14.92	0	1.99	73.06	0	8.4	1.59	0	7
212	1.52065	14.36	0	2.02	73.42	0	8.44	1.64	0	7
213	1.51651	14.38	0	1.94	73.61	0	8.48	1.57	0	7
214	1.51711	14.23	0	2.08	73.36	0	8.62	1.67	0	7

       PS：現在正在步入第四科學正規化，第一正規化是實驗（哥白尼），第二正規化是理論（牛頓），第三正規化是計算（四色填充地圖），第四正規化是資料。


三. 迴歸模型分析

        迴歸模型分析程式碼如下：
        注意：1) pandas、Matplotlib、seaboard三種不同方法繪製圖形，基本類似。
                   2) 程式碼對應結果不進行詳細分析，只提供方法，為提升學生閱讀程式碼能力。

# -*- coding: utf-8 -*-
"""
Created on Sun Mar 05 18:10:07 2017

@author: eastmount & zj
"""

#匯入玻璃識別資料集
import pandas as pd
glass=pd.read_csv("glass.csv")
#顯示前6行資料
print(glass.shape)
print(glass.head(6))

import seaborn as sns
import matplotlib.pyplot as plt
sns.set(font_scale=1.5)
sns.lmplot(x='al', y='ri', data=glass, ci=None)
#利用Pandas畫散點圖
glass.plot(kind='scatter', x='al', y='ri')
plt.show()

#利用matplotlib做等效的散點圖
plt.scatter(glass.al, glass.ri)
plt.xlabel('al')
plt.ylabel('ri')

#擬合線性迴歸模型
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
feature_cols = ['al']
X = glass[feature_cols]
y = glass.ri
linreg.fit(X, y)
plt.show()

#對於所有的x值做出預測       
glass['ri_pred'] = linreg.predict(X)
print("預測的前六行:")
print(glass.head(6))

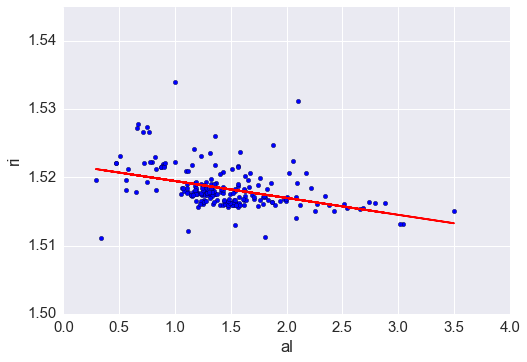
#用直線表示預測結果
plt.plot(glass.al, glass.ri_pred, color='red')
plt.xlabel('al')
plt.ylabel('Predicted ri')
plt.show()

#將直線結果和散點圖同時顯示出來
plt.scatter(glass.al, glass.ri)
plt.plot(glass.al, glass.ri_pred, color='red')
plt.xlabel('al')
plt.ylabel('ri')
plt.show()

#利用相關方法線性預測
linreg.intercept_ + linreg.coef_ * 2
#使用預測方法計算Al = 2的預測
linreg.predict(2)

#鋁檢驗係數
ai=zip(feature_cols, linreg.coef_)
print(ai)

#使用預測方法計算Al = 3的預測
pre=linreg.predict(3)
print(pre)

#檢查glass_type
sort=glass.glass_type.value_counts().sort_index()
print(sort)

#型別1、2、3的窗戶玻璃
#型別5，6，7是家用玻璃
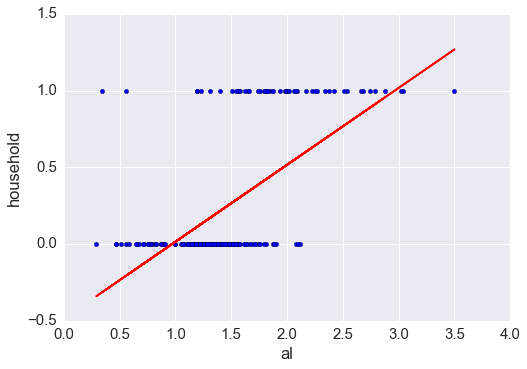
glass['household'] = glass.glass_type.map({1:0, 2:0, 3:0, 5:1, 6:1, 7:1})
print(glass.head())

plt.scatter(glass.al, glass.household)
plt.xlabel('al')
plt.ylabel('household')
plt.show()

#擬合線性迴歸模型並儲存預測
feature_cols = ['al']
X = glass[feature_cols]
y = glass.household
linreg.fit(X, y)
glass['household_pred'] = linreg.predict(X)
plt.show()

#包括迴歸線的散點圖
plt.scatter(glass.al, glass.household)
plt.plot(glass.al, glass.household_pred, color='red')
plt.xlabel('al')
plt.ylabel('household')
plt.show()
        輸出結果如下：
預測的前六行:
   id       ri     na    mg    al     si     k    ca   ba    fe  glass_type  \
0   1  1.52101  13.64  4.49  1.10  71.78  0.06  8.75  0.0  0.00           1   
1   2  1.51761  13.89  3.60  1.36  72.73  0.48  7.83  0.0  0.00           1   
2   3  1.51618  13.53  3.55  1.54  72.99  0.39  7.78  0.0  0.00           1   
3   4  1.51766  13.21  3.69  1.29  72.61  0.57  8.22  0.0  0.00           1   
4   5  1.51742  13.27  3.62  1.24  73.08  0.55  8.07  0.0  0.00           1   
5   6  1.51596  12.79  3.61  1.62  72.97  0.64  8.07  0.0  0.26           1   

    ri_pred  
0  1.519220  
1  1.518576  
2  1.518130  
3  1.518749  
4  1.518873  
5  1.517932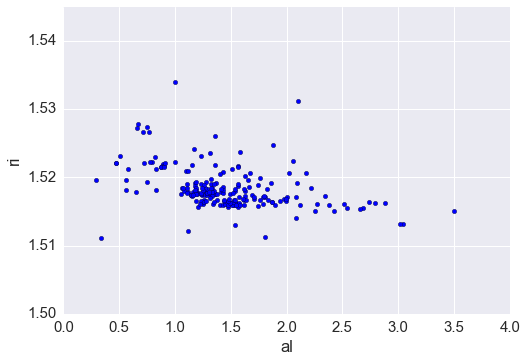
        部分輸出如下圖所示，繪製圖形al和ri基本點狀圖：



        將預測的線性迴歸直線結果和散點圖同時顯示出來：




        擬合邏輯迴歸程式碼：

# -*- coding: utf-8 -*-
"""
Created on Sun Mar 05 18:28:56 2017

@author: eastmount & zj
"""

#-------------邏輯迴歸-----------------

#擬合Logistic迴歸模型，儲存類預測
import numpy as np
nums = np.array([5, 15, 8])
np.where(nums > 10, 'big', 'small')  


#將household_pred轉換為 1或0   
glass['household_pred_class'] = np.where(glass.household_pred >= 0.5, 1, 0)
print(glass.head(6))
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression(C=1e9)
feature_cols = ['al']
X = glass[feature_cols]
y = glass.household
logreg.fit(X, y)
glass['household_pred_class'] = logreg.predict(X)


#繪圖-顯示預測結果
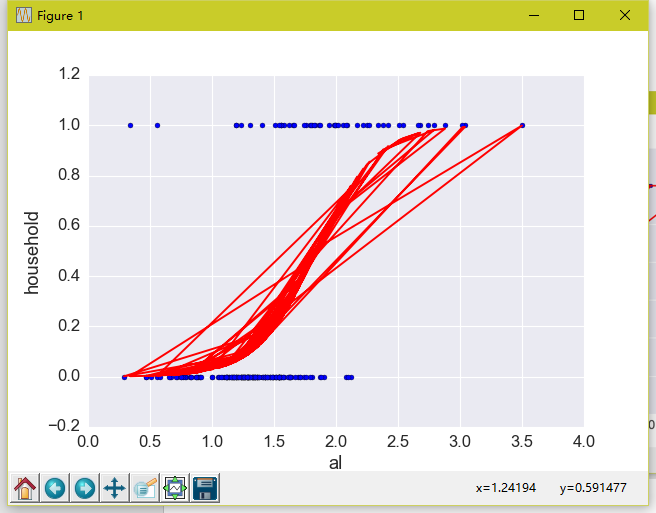
plt.scatter(glass.al, glass.household)
plt.plot(glass.al, glass.household_pred_class, color='red')
plt.xlabel('al')
plt.ylabel('household')
plt.show()

glass['household_pred_prob'] = logreg.predict_proba(X)[:, 1]
#繪圖 繪製預測概率

plt.scatter(glass.al, glass.household)
plt.plot(glass.al, glass.household_pred_prob, color='red')
plt.xlabel('al')
plt.ylabel('household')
plt.show()

#檢查一些例子的預測
print (logreg.predict_proba (1))
print (logreg.predict_proba(2))
print (logreg. predict_proba (3))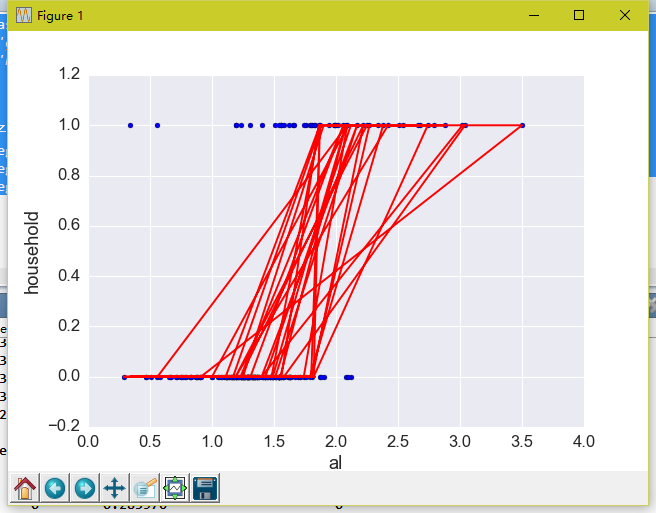
輸出如下圖所示：





        最後希望這篇文章對你有所幫助，尤其是我的學生和接觸資料探勘、機器學習的博友。新學期開始，各種事情，專注教學、科研及專案，加油~
        愛你的一切，伴著尤克里裡的琴聲寫了一下午，謝謝我的女神。
       (By:Eastmount 2017-03-05 下午6點半  http://blog.csdn.net/eastmount/ )


相關文章