【Python資料探勘課程】八.關聯規則挖掘及Apriori實現購物推薦

Eastmount發表於2016-11-28
Python
        這篇文章主要介紹三個知識點，也是我《資料探勘與分析》課程講課的內容。
        1.關聯規則挖掘概念及實現過程；
        2.Apriori演算法挖掘頻繁項集；
        3.Python實現關聯規則挖掘及置信度、支援度計算。

        前文推薦：
       【Python資料探勘課程】一.安裝Python及爬蟲入門介紹
       【Python資料探勘課程】二.Kmeans聚類資料分析及Anaconda介紹
       【Python資料探勘課程】三.Kmeans聚類程式碼實現、作業及優化
       【Python資料探勘課程】四.決策樹DTC資料分析及鳶尾資料集分析
       【Python資料探勘課程】五.線性迴歸知識及預測糖尿病例項
       【Python資料探勘課程】六.Numpy、Pandas和Matplotlib包基礎知識
       【Python資料探勘課程】七.PCA降維操作及subplot子圖繪製

        希望這篇文章對你有所幫助，尤其是剛剛接觸資料探勘以及大資料的同學，這些基礎知識真的非常重要。如果文章中存在不足或錯誤的地方，還請海涵~
        參考：
        關聯規則挖掘之Apriori演算法實現超市購物 - eastmount
        關聯規則簡介與Apriori演算法 - 百度文庫guaidaoK


一. 關聯規則挖掘概念及實現過程

        1.關聯規則
        關聯規則（Association Rules）是反映一個事物與其他事物之間的相互依存性和關聯性，如果兩個或多個事物之間存在一定的關聯關係，那麼，其中一個事物就能通過其他事物預測到。關聯規則是資料探勘的一個重要技術，用於從大量資料中挖掘出有價值的資料項之間的相關關係。
        關聯規則首先被Agrawal, lmielinski and Swami在1993年的SIGMOD會議上提出。
        關聯規則挖掘的最經典的例子就是沃爾瑪的啤酒與尿布的故事，通過對超市購物籃資料進行分析，即顧客放入購物籃中不同商品之間的關係來分析顧客的購物習慣，發現美國婦女們經常會叮囑丈夫下班後為孩子買尿布，30%-40%的丈夫同時會順便購買喜愛的啤酒，超市就把尿布和啤酒放在一起銷售增加銷售額。有了這個發現後，超市調整了貨架的設定，把尿布和啤酒擺放在一起銷售，從而大大增加了銷售額。

        2.常見案例
        前面講述了關聯規則挖掘對超市購物籃的例子，使用Apriori對資料進行頻繁項集挖掘與關聯規則的產生是一個非常有用的技術，其中我們眾所周知的例子如：
        (1) 沃爾瑪超市的尿布與啤酒
        (2) 超市的牛奶與麵包
        (3) 百度文庫推薦相關文件
        (4) 淘寶推薦相關書籍
        (5) 醫療推薦可能的治療組合
        (6) 銀行推薦相關聯業務
        這些都是商務智慧和關聯規則在實際生活中的運用。

        
        3.置信度與支援度
        (1) 什麼是規則？
        規則形如"如果…那麼…(If…Then…)"，前者為條件，後者為結果。例如一個顧客，如果買了可樂，那麼他也會購買果汁。
        如何來度量一個規則是否夠好？有兩個量，置信度（Confidence）和支援度（Support），假如存在如下表的購物記錄。

        (2) 基本概念
        關聯規則挖掘是尋找給定資料集中項之間的有趣聯絡。如下圖所示：


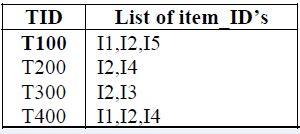
        其中，I={ I1, I2, … Im } 是m個不同專案的集合,集合中的元素稱為專案（Item）。
        專案的集合I稱為專案集合（Itemset），長度為k的項整合為k-項集（k-Itemset）。
        設任務相關的資料D是資料庫事務的集合，其中每個事務T是項的集合，使得T⊆I。每個事務有一個識別符號TID；設A是一個項集，事務T包含A當且僅當A⊆I，則關聯規則形式為A=>B（其中A⊂I，B⊂I，並且A∩B= ∅），交易集D中包含交易的個數記為|D|。

        在關聯規則度量中有兩個重要的度量值：支援度和置信度。
        對於關聯規則R:A=>B，則：
        支援度（suppport）：是交易集中同時包含A和B的交易數與所有交易數之比。
                            Support(A=>B)=P(A∪B)=count(A∪B)/|D|
        置信度（confidence）：是包含A和B交易數與包含A的交易數之比。
                            Confidence(A=>B)=P(B|A)=support(A∪B)/support(A)

        (3) 支援度
        支援度（Support）計算在所有的交易集中，既有A又有B的概率。例如在5條記錄中，既有橙汁又有可樂的記錄有2條。則此條規則的支援度為 2/5=0.4，即：
                                               Support(A=>B)=P(AB)
        現在這條規則可表述為，如果一個顧客購買了橙汁，則有50%(置信度)的可能購買可樂。而這樣的情況（即買了橙汁會再買可樂）會有40%（支援度）的可能發生。 



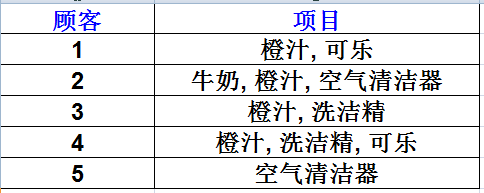
        (4) 置信度
        置信度（confidence）表示了這條規則有多大程度上值得可信。設條件的項的集合為A,結果的集合為B。置信度計算在A中，同時也含有B的概率（即：if A ,then B的概率）。即 ：
                                               Confidence(A=>B)=P(B|A)
        例如計算“如果Orange則Coke”的置信度。由於在含有“橙汁”的4條交易中，僅有2條交易含有“可樂”，其置信度為0.5。

        (5) 最小支援度與頻繁集
        發現關聯規則要求項集必須滿足的最小支援閾值，稱為項集的最小支援度（Minimum Support），記為supmin。支援度大於或等於supmin的項集稱為頻繁項集，簡稱頻繁集，反之則稱為非頻繁集。通常k-項集如果滿足supmin，稱為k-頻繁集，記作Lk。關聯規則的最小置信度（Minimum Confidence）記為confmin，它表示關聯規則需要滿足的最低可靠性。

        (6) 關聯規則







        (7) 強關聯規則
        如果規則R：X=>Y 滿足 support(X=>Y) >= supmin 且 confidence(X=>Y)>=confmin，稱關聯規則X=>Y為強關聯規則，否則稱關聯規則X=>Y為弱關聯規則。
        在挖掘關聯規則時，產生的關聯規則要經過supmin和confmin的衡量，篩選出來的強關聯規則才能用於指導商家的決策。



二. Apriori演算法挖掘頻繁項集

        關聯規則對購物籃進行挖掘，通常採用兩個步驟進行：
        a.找出所有頻繁項集（文章中我使用Apriori演算法>=最小支援度的項集）
        b.由頻繁項集產生強關聯規則，這些規則必須大於或者等於最小支援度和最小置信度。
        下面將通超市購物的例子對關聯規則挖掘Apriori演算法進行分析。

        Apriori演算法是一種對有影響的挖掘布林關聯規則頻繁項集的演算法，通過演算法的連線和剪枝即可挖掘頻繁項集。
        Apriori演算法將發現關聯規則的過程分為兩個步驟：
        1.通過迭代，檢索出事務資料庫中的所有頻繁項集，即支援度不低於使用者設定的閾值的項集；
        2.利用頻繁項集構造出滿足使用者最小置信度的規則。
        挖掘或識別出所有頻繁項集是該演算法的核心，佔整個計算量的大部分。 



        補充頻繁項集相關知識：
        K-項集：指包含K個項的項集；
        項集的出現頻率：指包含項集的事務數，簡稱為項集的頻率、支援度計數或計數；
        頻繁項集：如果項集的出現頻率大於或等於最小支援度計數閾值，則稱它為頻繁項集，其中頻繁K-項集的集合通常記作Lk。
        下面直接通過例子描述該演算法：如下圖所示，使用Apriori演算法關聯規則挖掘資料集中的頻繁項集。（最小支援度計數為2）

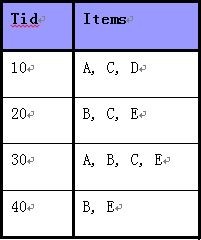
        具體過程如下所示：

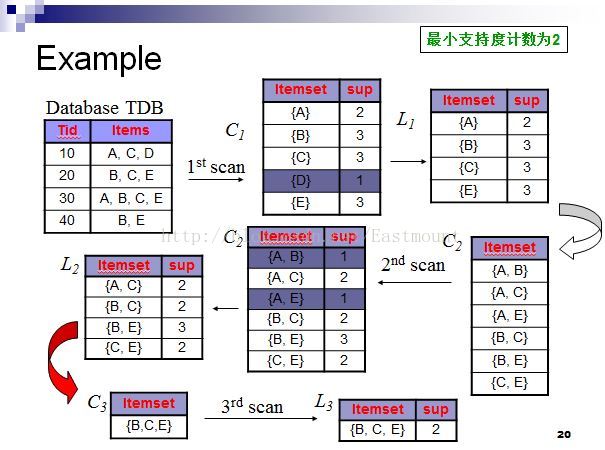
        具體分析結果：
        第一次掃描：對每個候選商品計數得C1，由於候選{D}支援度計數為1<最小支援度計數2，故刪除{D}得頻繁1-項集合L1；
        第二次掃描：由L1產生候選C2並對候選計數得C2，比較候選支援度計數與最小支援度計數2得頻繁2-項集合L2；
        第三次掃描：用Apriori演算法對L2進行連線和剪枝產生候選3項集合C3的過程如下：
        1.連線：
        C3=L2\bowtie(連線)L2={{A,C},{B,C},{B,E},{C,E}}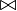\bowtie{{A,C},{B,C},{B,E},{C,E}}={{A,B,C},{A,C,E},{B,C,E}}
        2.剪枝：
        {A,B,C}的2項子集{A,B},{A,C}和{B,C}，其中{A,B}不是2項子集L2，因此不是頻繁的，從C3中刪除；
        {A,C,E}的2項子集{A,C},{A,E}和{C,E}，其中{A,E}不是2項子集L2，因此不是頻繁的，從C3中刪除；
        {B,C,E}的2項子集{B,C},{B,E}和{C,E}，它的所有2項子集都是L2的元素，保留C3中。
        經過Apriori演算法對L2連線和剪枝後產生候選3項集的集合為C3={B,C,E}. 在對該候選商品計數，由於等於最小支援度計數2，故得頻繁3-項集合L3，同時由於4-項集中僅1個，故C4為空集，演算法終止。



三. 舉例：頻繁項集產生強關聯規則

        強關聯規：如果規則R：X=>Y滿足support(X=>Y)>=supmin(最小支援度，它用於衡量規則需要滿足的最低重要性)且confidence(X=>Y)>=confmin（最小置信度，它表示關聯規則需要滿足的最低可靠性）稱關聯規則X=>Y為強關聯規則，否則稱關聯規則X=>Y為弱關聯規則。
        例子：
        現有A、B、C、D、E五種商品的交易記錄表，找出所有頻繁項集，假設最小支援度>=50%，最小置信度>=50%。
        對於關聯規則R：A=>B，則：
        支援度（suppport）：是交易集中同時包含A和B的交易數與所有交易數之比。
                            Support(A=>B)=P(A∪B)=count(A∪B)/|D|
        置信度（confidence）：是包含A和B交易數與包含A的交易數之比。
                            Confidence(A=>B)=P(B|A)=support(A∪B)/support(A)


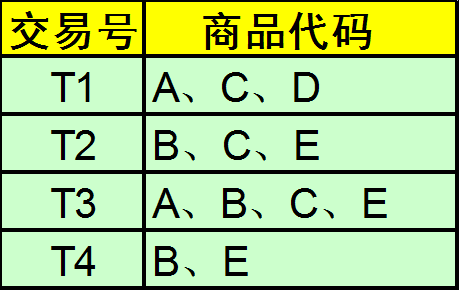
        計算過程如下，K=1的時候項集{A}在T1、T3中出現2次，共4條交易，故支援度為2/4=50%，依次計算。其中項集{D}在T1出現，其支援度為1/4=25%，小於最小支援度50%，故去除，得到L1。
        然後對L1中項集兩兩組合，再分別計算其支援度，其中項集{A, B}在T3中出現1次，其支援度=1/4=25%，小於最小支援度50%，故去除，同理得到L2項集。



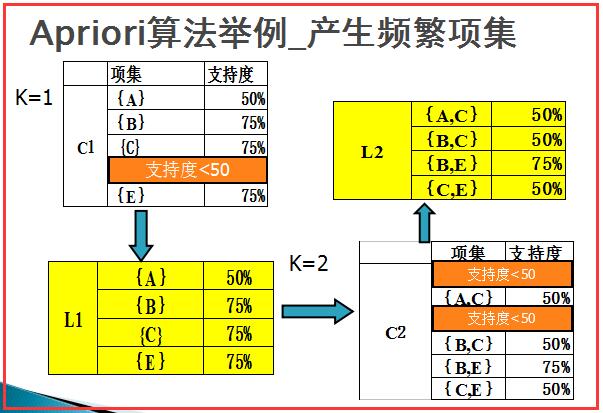
        然後如下圖所示，對L2中的項集進行組合，其中超過三項的進行過濾，最後計算得到L3項集{B，C，E}。


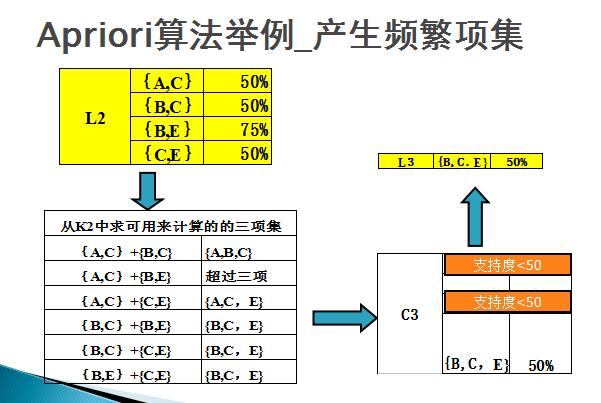
        最後對計算置信度，如下圖所示。


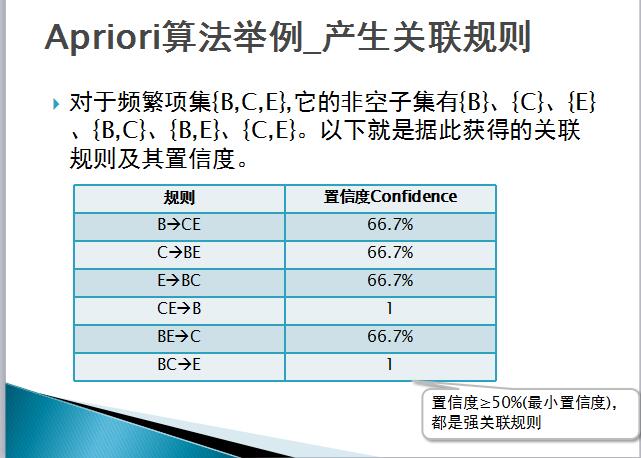
        Apriori演算法弊端：需要多次掃描資料表。如果頻繁集最多包含10個項，那麼就需要掃描交易資料表10遍，這需要很大的I/O負載。同時，產生大量頻繁集，若有100個專案，可能產生候選項數目。
        故：Jiawei Han等人在2000年提出了一種基於FP-樹的關聯規則挖掘演算法FP_growth，它採取“分而治之”的策略，將提供頻繁專案集的資料庫壓縮成一棵頻繁模式樹（FP-樹）。
        推薦一張圖，詳細分析關聯規則的過程：



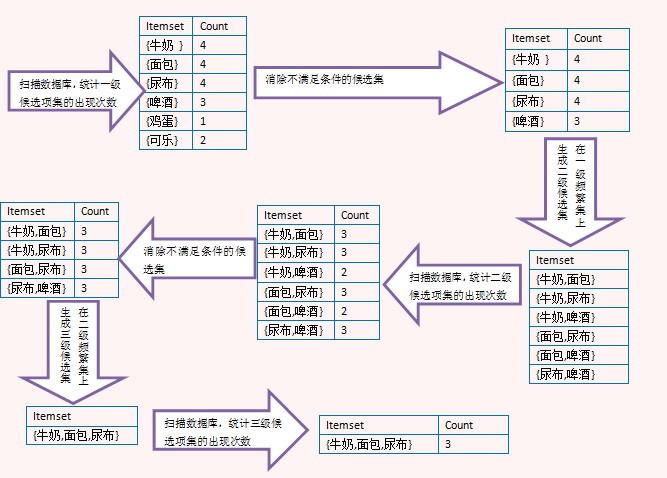
        參考文獻：
        [1]高明 . 關聯規則挖掘演算法的研究及其應用[D].山東師範大學. 2006
        [2]李彥偉 . 基於關聯規則的資料探勘方法研究[D].江南大學. 2011
        [3]肖勁橙，林子禹，毛超.關聯規則在零售商業的應用[J].計算機工程.2004,30(3):189-190.
        [4]秦亮曦，史忠植.關聯規則研究綜述[J].廣西大學學報.2005,30(4):310-317.
        [5]陳志泊，韓慧，王建新，孫俏，聶耿青．資料倉儲與資料探勘[M].北京：清華大學出版社.2009.
        [6]沈良忠.關聯規則中Apriori 演算法的C#實現研究[J].電腦知識與技術.2009,5(13):3501-3504.
        [7]趙衛東.商務智慧(第二版)[M].北京：清華大學出版社.2011.


四. Python實現關聯規則挖掘及置信度、支援度計算

        由於這部分程式碼在Sklearn中沒有相關庫，自己後面會實現並替換，目前參考空木大神的部落格。地址：http://blog.csdn.net/u010454729/article/details/49078505

# -*- coding: utf-8 -*-
"""
Created on Mon Nov 28 03:29:51 2016

地址：http://blog.csdn.net/u010454729/article/details/49078505

@author: 參考CSDN u010454729 
"""

# coding=utf-8  
def  loadDataSet():  
    return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]  
  
def createC1(dataSet):                  #構建所有候選項集的集合  
    C1 = []  
    for transaction in dataSet:  
        for item in transaction:  
            if not [item] in C1:  
                C1.append([item])       #C1新增的是列表，對於每一項進行新增，{1},{3},{4},{2},{5}  
    C1.sort()  
    return map(frozenset, C1)           #使用frozenset，被“冰凍”的集合，為後續建立字典key-value使用。  
  
def scanD(D,Ck,minSupport):             #由候選項集生成符合最小支援度的項集L。引數分別為資料集、候選項集列表，最小支援度  
    ssCnt = {}  
    for tid in D:                       #對於資料集裡的每一條記錄  
        for can in Ck:                  #每個候選項集can  
            if can.issubset(tid):       #若是候選集can是作為記錄的子集，那麼其值+1,對其計數  
                if not ssCnt.has_key(can):#ssCnt[can] = ssCnt.get(can,0)+1一句可破，沒有的時候為0,加上1,有的時候用get取出，加1  
                    ssCnt[can] = 1  
                else:  
                    ssCnt[can] +=1  
    numItems = float(len(D))    
    retList  = []  
    supportData = {}  
    for key in ssCnt:  
        support = ssCnt[key]/numItems   #除以總的記錄條數，即為其支援度  
        if support >= minSupport:  
            retList.insert(0,key)       #超過最小支援度的項集，將其記錄下來。  
        supportData[key] = support  
    return retList, supportData  
  
def aprioriGen(Lk, k):                  #建立符合置信度的項集Ck,  
    retList = []  
    lenLk   = len(Lk)  
    for i in range(lenLk):  
        for j in range(i+1, lenLk):     #k=3時，[:k-2]即取[0],對{0,1},{0,2},{1,2}這三個項集來說，L1=0，L2=0，將其合併得{0,1,2}，當L1=0,L2=1不新增，  
            L1 = list(Lk[i])[:k-2]  
            L2 = list(Lk[j])[:k-2]  
            L1.sort()  
            L2.sort()  
            if L1==L2:  
                retList.append(Lk[i]|Lk[j])  
    return retList  
  
def apriori(dataSet, minSupport = 0.5):  
    C1 = createC1(dataSet)  
    D  = map(set,dataSet)  
    L1, supportData = scanD(D,C1,minSupport)  
    L  = [L1]                           #L將包含滿足最小支援度，即經過篩選的所有頻繁n項集，這裡新增頻繁1項集  
    k  = 2  
    while (len(L[k-2])>0):              #k=2開始，由頻繁1項集生成頻繁2項集，直到下一個打的項集為空  
        Ck = aprioriGen(L[k-2], k)  
        Lk, supK = scanD(D, Ck, minSupport)  
        supportData.update(supK)        #supportData為字典，存放每個項集的支援度，並以更新的方式加入新的supK  
        L.append(Lk)  
        k +=1  
    return L,supportData  
  
dataSet = loadDataSet()  
C1 = createC1(dataSet)  
print "所有候選1項集C1:\n",C1  
  
D = map(set, dataSet)  
print "資料集D:\n",D  
  
L1, supportData0 = scanD(D,C1, 0.5)  
print "符合最小支援度的頻繁1項集L1:\n",L1  
  
L, suppData = apriori(dataSet)  
print "所有符合最小支援度的項集L：\n",L  
print "頻繁2項集：\n",aprioriGen(L[0],2)  
L, suppData = apriori(dataSet, minSupport=0.7)  
print "所有符合最小支援度為0.7的項集L：\n",L
        輸出結果：
所有候選1項集C1:
[frozenset([1]), frozenset([2]), frozenset([3]), frozenset([4]), frozenset([5])]
資料集D:
[set([1, 3, 4]), set([2, 3, 5]), set([1, 2, 3, 5]), set([2, 5])]
符合最小支援度的頻繁1項集L1:
[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])]
所有符合最小支援度的項集L：
[[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])], [frozenset([1, 3]), frozenset([2, 5]), 
frozenset([2, 3]), frozenset([3, 5])], [frozenset([2, 3, 5])], []]
頻繁2項集：
[frozenset([1, 3]), frozenset([1, 2]), frozenset([1, 5]), frozenset([2, 3]), frozenset([3, 5]), frozenset([2, 5])]
所有符合最小支援度為0.7的項集L：
[[frozenset([3]), frozenset([2]), frozenset([5])], [frozenset([2, 5])], []]


        最後希望這篇文章對你有所幫助，尤其是我的學生和接觸資料探勘、機器學習的博友。星期天晚上和思華在辦公室寫到三點半，慶幸這麼好多可愛的學生，自己也在成長，經歷很多終究是好事，最近沉醉某些事中，希望能成真！加油~
       (By:Eastmount 2016-11-28 凌晨3點半  http://blog.csdn.net/eastmount/ )


相關文章