【Python資料探勘課程】五.線性迴歸知識及預測糖尿病例項
今天主要講述的內容是關於一元線性迴歸的知識,Python實現,包括以下內容:
1.機器學習常用資料集介紹
2.什麼是線性回顧
3.LinearRegression使用方法
4.線性迴歸判斷糖尿病
前文推薦:
【Python資料探勘課程】一.安裝Python及爬蟲入門介紹
【Python資料探勘課程】二.Kmeans聚類資料分析及Anaconda介紹
【Python資料探勘課程】三.Kmeans聚類程式碼實現、作業及優化
【Python資料探勘課程】四.決策樹DTC資料分析及鳶尾資料集分析
希望這篇文章對你有所幫助,尤其是剛剛接觸資料探勘以及大資料的同學,同時準備嘗試以案例為主的方式進行講解。如果文章中存在不足或錯誤的地方,還請海涵~
同時這篇文章是我上課的內容,所以參考了一些知識,強烈推薦大家學習史丹佛的機器學習Ng教授課程和Scikit-Learn中的內容。由於自己數學不是很好,自己也還在學習中,所以文章以程式碼和一元線性迴歸為主,數學方面的當自己學到一定的程度,才能進行深入的分享及介紹。抱歉~
一. 資料集介紹
1.diabetes dataset資料集
資料集參考:http://scikit-learn.org/stable/datasets/
這是一個糖尿病的資料集,主要包括442行資料,10個屬性值,分別是:Age(年齡)、性別(Sex)、Body mass index(體質指數)、Average Blood Pressure(平均血壓)、S1~S6一年後疾病級數指標。Target為一年後患疾病的定量指標。
輸出如下所示:
# -*- coding: utf-8 -*-
"""
Created on Thu Oct 27 02:37:05 2016
@author: yxz15
"""
from sklearn import datasets
diabetes = datasets.load_diabetes() #載入資料
print diabetes.data #資料
print diabetes.target #類標
print u'總行數: ', len(diabetes.data), len(diabetes.target) #資料總行數
print u'特徵數: ', len(diabetes.data[0]) #每行資料集維數
print u'資料型別: ', diabetes.data.shape #型別
print type(diabetes.data), type(diabetes.target) #資料集型別
"""
[[ 0.03807591 0.05068012 0.06169621 ..., -0.00259226 0.01990842
-0.01764613]
[-0.00188202 -0.04464164 -0.05147406 ..., -0.03949338 -0.06832974
-0.09220405]
...
[-0.04547248 -0.04464164 -0.0730303 ..., -0.03949338 -0.00421986
0.00306441]]
[ 151. 75. 141. 206. 135. 97. 138. 63. 110. 310. 101.
...
64. 48. 178. 104. 132. 220. 57.]
總行數: 442 442
特徵數: 10
資料型別: (442L, 10L)
<type 'numpy.ndarray'> <type 'numpy.ndarray'>
""" 2.sklearn常見資料集
常見的sklearn資料集包括,強烈推薦下面這篇文章:
http://blog.csdn.net/sa14023053/article/details/52086695
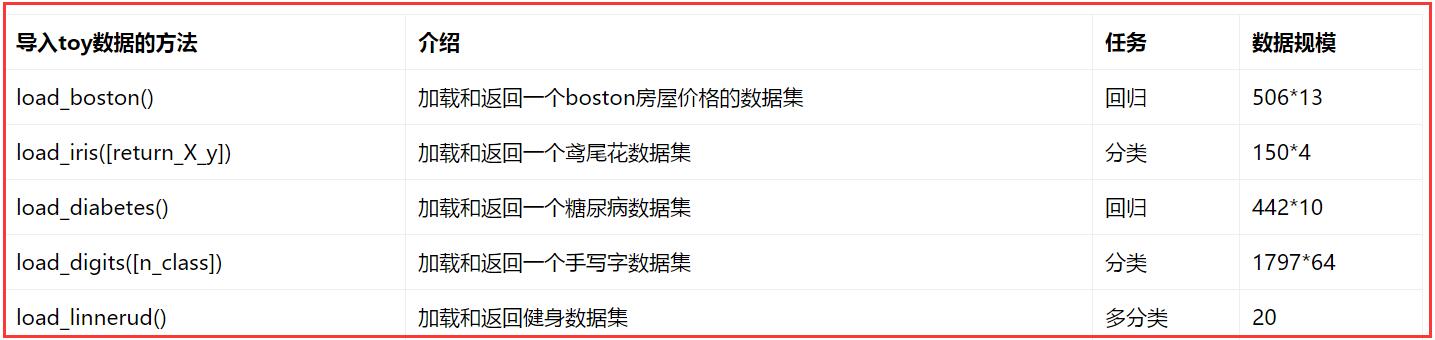
sklearn包含一些不許要下載的toy資料集,見下表,包括波士頓房屋資料集、鳶尾花資料集、糖尿病資料集、手寫字資料集和健身資料集等。
3.UCI資料集
常用資料集包括:http://archive.ics.uci.edu/ml/datasets.html

二. 什麼是線性迴歸
1.機器學習簡述
機器學習(Machine Learning )包括:
a.監督學習(Supervised Learning):迴歸(Regression)、分類(Classification)
例:訓練過程中知道結果。小孩給水果分類,給他蘋果告訴他是蘋果,反覆訓練學習。在給他說過,問他是什麼?他回答準確,如果是桃子,他不能回答為蘋果。
b.無監督學習(Unsupervised Learning):聚類(Clustering)
例:訓練過程中不知道結果。給小孩一堆水果,如蘋果、橘子、桃子,小孩開始不知道需要分類的水果是什麼,讓小孩對水果進行分類。分類完成後,給他一個蘋果,小孩應該把它放到蘋果堆中。
c.增強學習(Reinforcement Learning)
例:ML過程中,對行為做出評價,評價有正面的和負面兩種。通過學習評價,程式應做出更好評價的行為。
d.推薦系統(Recommender System)
2.史丹佛公開課:第二課 單變數線性迴歸
這是NG教授的很著名的課程,這裡主要引用52nlp的文章,真的太完美了。推薦閱讀該作者的更多文章:
Coursera公開課筆記: 史丹佛大學機器學習第二課"單變數線性迴歸(Linear regression with one variable)"
<1>模型表示(Model Representation)
房屋價格預測問題,有監督學習問題。每個樣本的輸入都有正確輸出或答案,它也是一個迴歸問題,預測一個真實值的輸出。
訓練集表示如下:
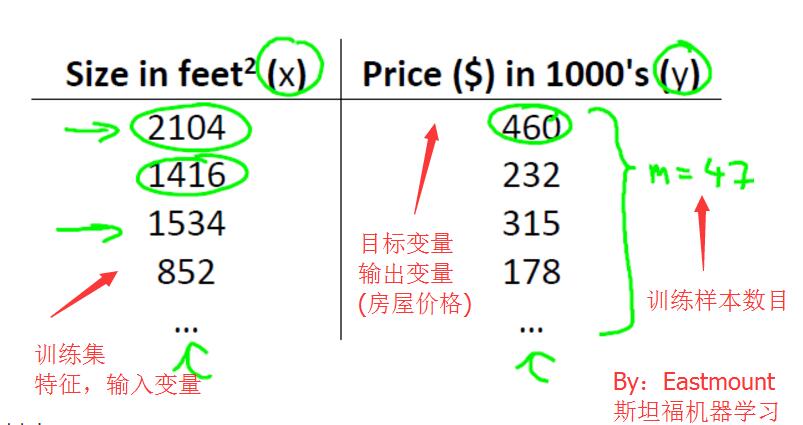
對於房價預測問題,訊息過程如下所示:
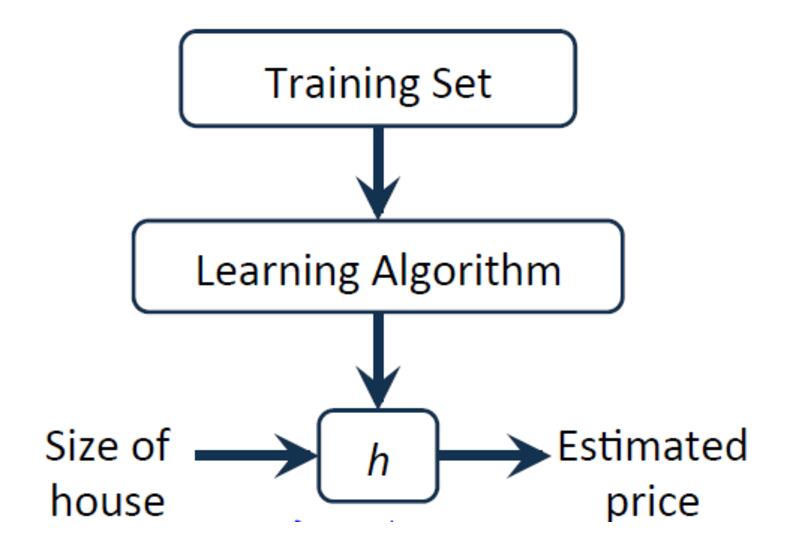
<2>成本函式(Cost Function)
對於上面的公式函式h(x),如何求theta0和theta1引數呢?
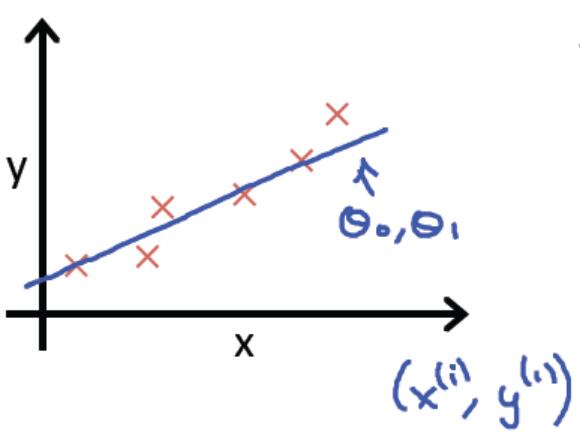
Cost Function可表示為:
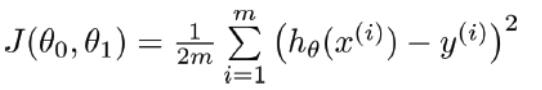
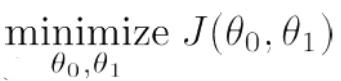
總的來說,線性迴歸主要包括一下四個部分,分別是Hypothesis、Parameters、Cost Function、Goal。右圖位簡化版,theta0賦值為0。

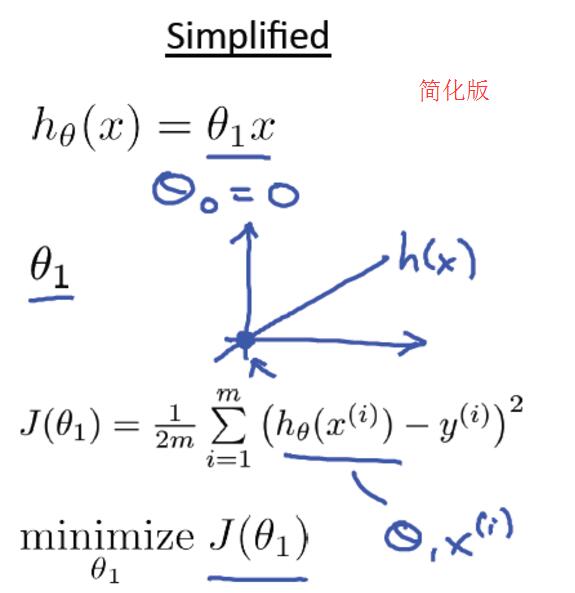
然後令θ1分別取1、0.5、-0.5等值,同步對比hθ(x)和J(θ0,θ1)在二維座標系中的變化情況,具體可參考原PPT中的對比圖,很直觀。
<3>梯度下降(Gradient descent)
應用的場景之一最小值問題:
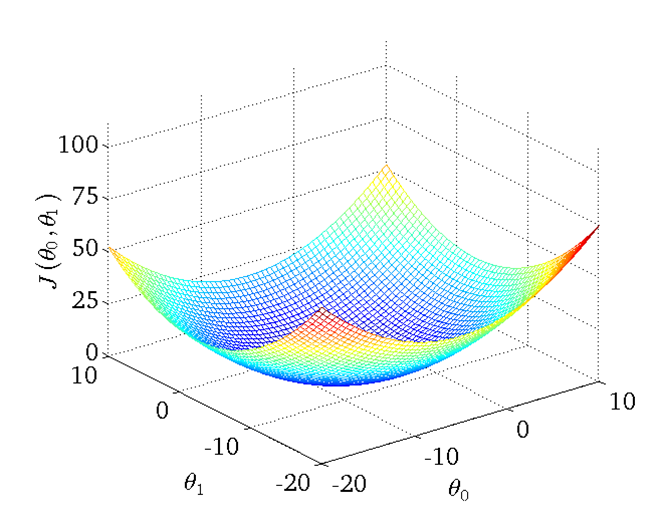
對於一些函式,例如J(θ0,θ1)
目標: minθ0,θ1J(θ0,θ1)
方法的框架:
a. 給θ0, θ1一個初始值,例如都等於0;
b. 每次改變θ0, θ1的時候都保持J(θ0,θ1)遞減,直到達到一個我們滿意的最小值;
對於任一J(θ0,θ1) , 初始位置不同,最終達到的極小值點也不同,例如以下例子:
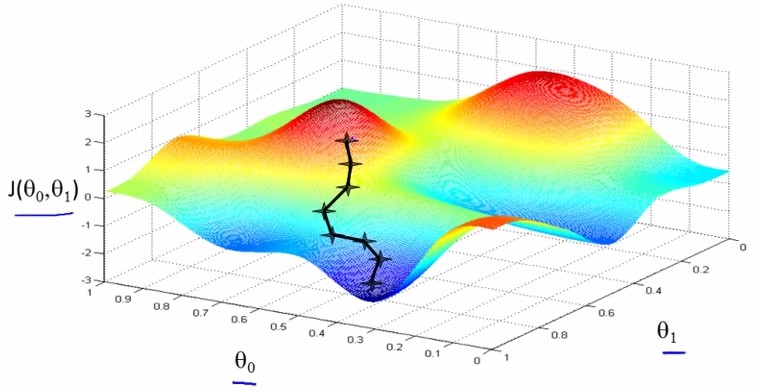
3.一元迴歸模型
轉自文章:http://blog.sina.com.cn/s/blog_68c81f3901019hhp.html
<1>什麼是線性迴歸?
迴歸函式的具體解釋和定義,可檢視任何一本“概率論與數理統計”的書。我看的是“陳希孺”的。
這裡我講幾點:
1)統計迴歸分析的任務,就在於根據 x1,x2,...,xp 線性迴歸和Y的觀察值,去估計函式f,尋求變數之間近似的函式關係。
2)我們常用的是,假定f函式的數學形式已知,其中若干個引數未知,要通過自變數和因變數的觀察值去估計未知的引數值。這叫“引數迴歸”。其中應用最廣泛的是f為線性函式的假設:
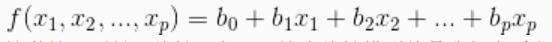
3)自變數只有一個時,叫做一元線性迴歸。
f(x) = b0+b1x
自變數有多個時,叫做多元線性迴歸。
f(x1,x2,...,xp) = b0 + b1x1 + b2x2 + ... + bpxp
4)分類(Classification)與迴歸(Regression)都屬於監督學習,他們的區別在於:
分類:用於預測有限的離散值,如是否得了癌症(0,1),或手寫數字的判斷,是0,1,2,3,4,5,6,7,8還是9等。分類中,預測的可能的結果是有限的,且提前給定的。
迴歸:用於預測實數值,如給定了房子的面積,地段,和房間數,預測房子的價格。
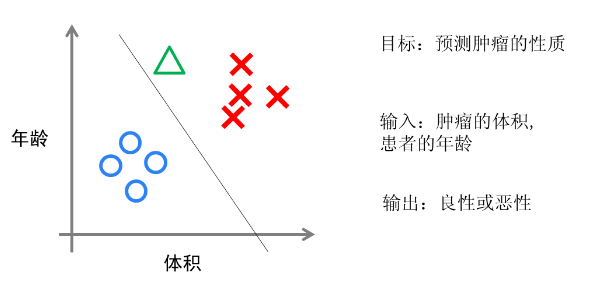
<2>一元線性迴歸
假設:我們要預測房價。當前自變數(輸入特徵)是房子面積x,因變數是房價y.給定了一批訓練集資料。我們要做的是利用手上的訓練集資料,得出x與y之間的函式f關係,並用f函式來預測任意麵積x對應的房價。
假設x與y是線性關係,則我們可以接著假設一元線性迴歸函式如下來代表y的預測值:
我們有訓練集了,那麼問題就成了如何利用現有的訓練集來判定未知引數 (θ0,θ1) 的值,使其讓h的值更接近實際值y? 訓練集指的是已知x,y值的資料集合!
一種方法是計算它的成本函式(Cost function),即預測出來的h的值與實際值y之間的方差的大小來決定當前的(θ0,θ1)值是否是最優的!
常用的成本函式是最小二乘法:
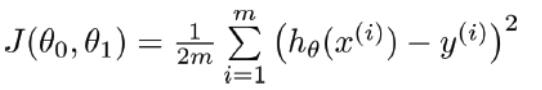

<3>模型總結
整個一元線性迴歸通過下面這張圖總結即可:

參考文章:史丹佛大學機器學習——線性迴歸(Linear Regression)
最後,梯度下降和多元迴歸模型將繼續學習,當我學到一定程度,再進行分享。
http://www.52nlp.cn/coursera公開課筆記-史丹佛大學機器學習第四課多變數
三. LinearRegression使用方法
LinearRegression模型在Sklearn.linear_model下,它主要是通過fit(x,y)的方法來訓練模型,其中x為資料的屬性,y為所屬型別。
sklearn中引用迴歸模型的程式碼如下:
from sklearn import linear_model #匯入線性模型
regr = linear_model.LinearRegression() #使用線性迴歸
print regr
輸出的函式原型如下所示:
LinearRegression(copy_X=True,
fit_intercept=True,
n_jobs=1,
normalize=False)predict(): 預測。它通過fit()算出的模型引數構成的模型,對解釋變數進行預測其類屬性。預測方法將返回預測值y_pred。
這裡推薦"搬磚小工053"大神的文章,非常不錯,強烈推薦。
引用他文章的例子,參考:scikit-learn : 線性迴歸,多元迴歸,多項式迴歸
# -*- coding: utf-8 -*-
"""
Created on Fri Oct 28 00:44:55 2016
@author: yxz15
"""
from sklearn import linear_model #匯入線性模型
import matplotlib.pyplot as plt #繪圖
import numpy as np
#X表示匹薩尺寸 Y表示匹薩價格
X = [[6], [8], [10], [14], [18]]
Y = [[7], [9], [13], [17.5], [18]]
print u'資料集X: ', X
print u'資料集Y: ', Y
#迴歸訓練
clf = linear_model.LinearRegression() #使用線性迴歸
clf.fit(X, Y) #匯入資料集
res = clf.predict(np.array([12]).reshape(-1, 1))[0] #預測結果
print(u'預測一張12英寸匹薩價格:$%.2f' % res)
#預測結果
X2 = [[0], [10], [14], [25]]
Y2 = clf.predict(X2)
#繪製線性迴歸圖形
plt.figure()
plt.title(u'diameter-cost curver') #標題
plt.xlabel(u'diameter') #x軸座標
plt.ylabel(u'cost') #y軸座標
plt.axis([0, 25, 0, 25]) #區間
plt.grid(True) #顯示網格
plt.plot(X, Y, 'k.') #繪製訓練資料集散點圖
plt.plot(X2, Y2, 'g-') #繪製預測資料集直線
plt.show()
資料集X: [[6], [8], [10], [14], [18]]
資料集Y: [[7], [9], [13], [17.5], [18]]
預測一張12英寸匹薩價格:$13.68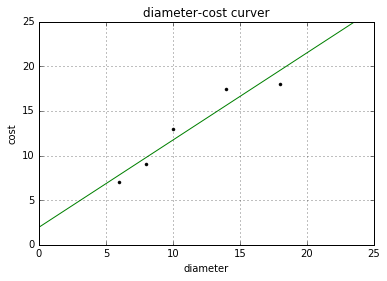
線性模型的迴歸係數W會儲存在他的coef_方法中,截距儲存在intercept_中。score(X,y,sample_weight=None) 評分函式,返回一個小於1的得分,可能會小於0。
print u'係數', clf.coef_
print u'截距', clf.intercept_
print u'評分函式', clf.score(X, Y)
'''
係數 [[ 0.9762931]]
截距 [ 1.96551743]
評分函式 0.910001596424
'''四. 線性迴歸判斷糖尿病
1.Diabetes資料集(糖尿病資料集)
糖尿病資料集包含442個患者的10個生理特徵(年齡,性別、體重、血壓)和一年以後疾病級數指標。
然後載入資料,同時將diabetes糖尿病資料集分為測試資料和訓練資料,其中測試資料為最後20行,訓練資料從0到-20行(不包含最後20行),即diabetes.data[:-20]。
from sklearn import datasets
#資料集
diabetes = datasets.load_diabetes() #載入資料
diabetes_x = diabetes.data[:, np.newaxis] #獲取一個特徵
diabetes_x_temp = diabetes_x[:, :, 2]
diabetes_x_train = diabetes_x_temp[:-20] #訓練樣本
diabetes_x_test = diabetes_x_temp[-20:] #測試樣本 後20行
diabetes_y_train = diabetes.target[:-20] #訓練標記
diabetes_y_test = diabetes.target[-20:] #預測對比標記
print u'劃分行數:', len(diabetes_x_temp), len(diabetes_x_train), len(diabetes_x_test)
print diabetes_x_test劃分行數: 442 422 20
[[ 0.07786339]
[-0.03961813]
[ 0.01103904]
[-0.04069594]
[-0.03422907]
[ 0.00564998]
[ 0.08864151]
[-0.03315126]
[-0.05686312]
[-0.03099563]
[ 0.05522933]
[-0.06009656]
[ 0.00133873]
[-0.02345095]
[-0.07410811]
[ 0.01966154]
[-0.01590626]
[-0.01590626]
[ 0.03906215]
[-0.0730303 ]]2.完整程式碼
改程式碼的任務是從生理特徵預測疾病級數,但僅獲取了一維特徵,即一元線性迴歸。【線性迴歸】的最簡單形式給資料集擬合一個線性模型,主要是通過調整一系列的參以使得模型的殘差平方和儘量小。
線性模型:y = βX+b
X:資料 y:目標變數 β:迴歸係數 b:觀測噪聲(bias,偏差)
參考文章:Linear Regression Example - Scikit-Learn
# -*- coding: utf-8 -*-
"""
Created on Fri Oct 28 01:21:30 2016
@author: yxz15
"""
from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
#資料集
diabetes = datasets.load_diabetes() #載入資料
#獲取一個特徵
diabetes_x_temp = diabetes.data[:, np.newaxis, 2]
diabetes_x_train = diabetes_x_temp[:-20] #訓練樣本
diabetes_x_test = diabetes_x_temp[-20:] #測試樣本 後20行
diabetes_y_train = diabetes.target[:-20] #訓練標記
diabetes_y_test = diabetes.target[-20:] #預測對比標記
#迴歸訓練及預測
clf = linear_model.LinearRegression()
clf.fit(diabetes_x_train, diabetes_y_train) #注: 訓練資料集
#係數 殘差平法和 方差得分
print 'Coefficients :\n', clf.coef_
print ("Residual sum of square: %.2f" %np.mean((clf.predict(diabetes_x_test) - diabetes_y_test) ** 2))
print ("variance score: %.2f" % clf.score(diabetes_x_test, diabetes_y_test))
#繪圖
plt.title(u'LinearRegression Diabetes') #標題
plt.xlabel(u'Attributes') #x軸座標
plt.ylabel(u'Measure of disease') #y軸座標
#點的準確位置
plt.scatter(diabetes_x_test, diabetes_y_test, color = 'black')
#預測結果 直線表示
plt.plot(diabetes_x_test, clf.predict(diabetes_x_test), color='blue', linewidth = 3)
plt.show() 執行結果如下所示,包括係數、殘差平方和、方差分數。
Coefficients :[ 938.23786125]
Residual sum of square: 2548.07
variance score: 0.47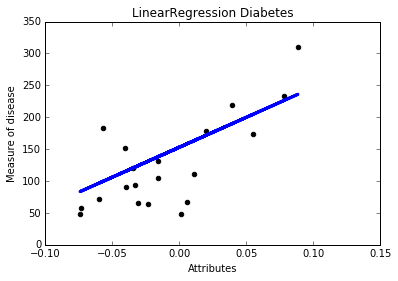
同時繪製圖形時,想去掉座標具體的值,可增加如下程式碼:
plt.xticks(())
plt.yticks(())五. 優化程式碼
下面是優化後的程式碼,增加了斜率、 截距的計算,同時增加了點圖到線性方程的距離,儲存圖片設定畫素。
# -*- coding: utf-8 -*-
"""
Created on Thu Dec 29 12:47:58 2011
@author: Administrator
"""
#第一步 資料集劃分
from sklearn import datasets
import numpy as np
#獲取資料 10*442
d = datasets.load_diabetes()
x = d.data
print u'獲取x特徵'
print len(x), x.shape
print x[:4]
#獲取一個特徵 第3列資料
x_one = x[:,np.newaxis, 2]
print x_one[:4]
#獲取的正確結果
y = d.target
print u'獲取的結果'
print y[:4]
#x特徵劃分
x_train = x_one[:-42]
x_test = x_one[-42:]
print len(x_train), len(x_test)
y_train = y[:-42]
y_test = y[-42:]
print len(y_train), len(y_test)
#第二步 線性迴歸實現
from sklearn import linear_model
clf = linear_model.LinearRegression()
print clf
clf.fit(x_train, y_train)
pre = clf.predict(x_test)
print u'預測結果'
print pre
print u'真實結果'
print y_test
#第三步 評價結果
cost = np.mean(y_test-pre)**2
print u'次方', 2**5
print u'平方和計算:', cost
print u'係數', clf.coef_
print u'截距', clf.intercept_
print u'方差', clf.score(x_test, y_test)
#第四步 繪圖
import matplotlib.pyplot as plt
plt.title("diabetes")
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x_test, y_test, 'k.')
plt.plot(x_test, pre, 'g-')
for idx, m in enumerate(x_test):
plt.plot([m, m],[y_test[idx],
pre[idx]], 'r-')
plt.savefig('power.png', dpi=300)
plt.show()
獲取x特徵
442 (442L, 10L)
[[ 0.03807591 0.05068012 0.06169621 0.02187235 -0.0442235 -0.03482076
-0.04340085 -0.00259226 0.01990842 -0.01764613]
[-0.00188202 -0.04464164 -0.05147406 -0.02632783 -0.00844872 -0.01916334
0.07441156 -0.03949338 -0.06832974 -0.09220405]
[ 0.08529891 0.05068012 0.04445121 -0.00567061 -0.04559945 -0.03419447
-0.03235593 -0.00259226 0.00286377 -0.02593034]
[-0.08906294 -0.04464164 -0.01159501 -0.03665645 0.01219057 0.02499059
-0.03603757 0.03430886 0.02269202 -0.00936191]]
[[ 0.06169621]
[-0.05147406]
[ 0.04445121]
[-0.01159501]]
獲取的結果
[ 151. 75. 141. 206.]
400 42
400 42
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
預測結果
[ 196.51241167 109.98667708 121.31742804 245.95568858 204.75295782
270.67732703 75.99442421 241.8354155 104.83633574 141.91879342
126.46776938 208.8732309 234.62493762 152.21947611 159.42995399
161.49009053 229.47459628 221.23405012 129.55797419 100.71606266
118.22722323 168.70056841 227.41445974 115.13701842 163.55022706
114.10695016 120.28735977 158.39988572 237.71514243 121.31742804
98.65592612 123.37756458 205.78302609 95.56572131 154.27961264
130.58804246 82.17483382 171.79077322 137.79852034 137.79852034
190.33200206 83.20490209]
真實結果
[ 175. 93. 168. 275. 293. 281. 72. 140. 189. 181. 209. 136.
261. 113. 131. 174. 257. 55. 84. 42. 146. 212. 233. 91.
111. 152. 120. 67. 310. 94. 183. 66. 173. 72. 49. 64.
48. 178. 104. 132. 220. 57.]
次方 32
平方和計算: 83.192340827
係數 [ 955.70303385]
截距 153.000183957
方差 0.427204267067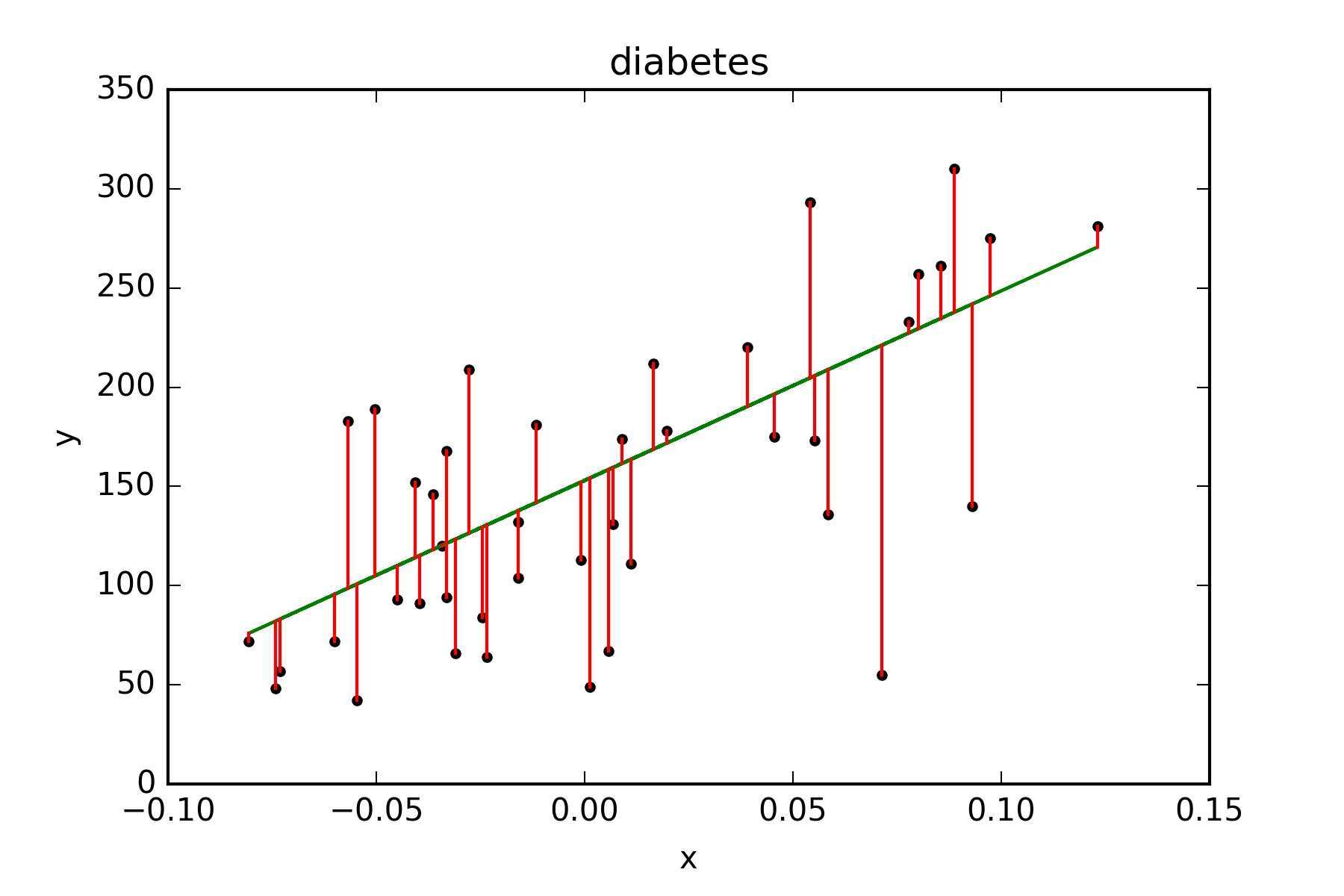
強烈推薦下面線性迴歸相關的文章,希望讀者自行閱讀:
[譯]針對科學資料處理的統計學習教程(scikit-learn教程2)Tacey Wong (重點)
scikit-learn : 線性迴歸 - 搬磚小工053
結合Scikit-learn介紹幾種常用的特徵選擇方法 - Bryan
用Python開始機器學習(3:資料擬合與廣義線性迴歸) - lsldd
Scikit Learn: 在python中機器學習 - yyliu
Python機器學習——線性模型 - 郝智恆
sklearn 資料載入工具(1) - 搬磚小工053
sklearn系列之----線性迴歸 - Gavin__Zhou
希望文章對你有所幫助,上課內容還需要繼續探索,這篇文章更希望你關注的是Python程式碼如何實現的,因為數學不好,所以詳細的推導過程,建議看文中的連結。
(By:Eastmount 2016-10-28 半夜3點半 http://blog.csdn.net/eastmount/ )
相關文章
- 【python資料探勘課程】十八.線性迴歸及多項式迴歸分析四個案例分享Python
- 【python資料探勘課程】十九.鳶尾花資料集視覺化、線性迴歸、決策樹花樣分析Python視覺化
- 【機器學習】線性迴歸預測機器學習
- 【python資料探勘課程】十六.邏輯迴歸LogisticRegression分析鳶尾花資料Python邏輯迴歸
- 資料探勘從入門到放棄(一):線性迴歸和邏輯迴歸邏輯迴歸
- 【Python資料探勘課程】九.迴歸模型LinearRegression簡單分析氧化物資料Python模型
- 【Python資料探勘課程】六.Numpy、Pandas和Matplotlib包基礎知識Python
- 【python資料探勘課程】二十三.時間序列金融資料預測及Pandas庫詳解Python
- 資料分析:線性迴歸
- 資料探勘比賽預備知識
- 預測演算法之多元線性迴歸演算法
- 採用線性迴歸實現訓練和預測(Python)Python
- 線性迴歸-如何對資料進行迴歸分析
- 【python資料探勘課程】二十二.Basemap地圖包安裝入門及基礎知識講解Python地圖
- 預測數值型資料:迴歸
- 【python資料探勘課程】十三.WordCloud詞雲配置過程及詞頻分析PythonCloud
- Stanford機器學習課程筆記——多變數線性迴歸模型機器學習筆記變數模型
- 使用線性迴歸模型預測黃金ETF價格模型
- 線性迴歸—求解介紹及迴歸擴充套件套件
- python實現線性迴歸之簡單迴歸Python
- 線性迴歸
- 支援向量機原理(五)線性支援迴歸
- 【機器學習】線性迴歸python實現機器學習Python
- 【Python資料探勘課程】七.PCA降維操作及subplot子圖繪製PythonPCA
- 機器學習-線性迴歸機器學習
- 1.3 - 線性迴歸
- 機器學習:線性迴歸機器學習
- 資料探勘之預測篇
- Alink漫談(十) :線性迴歸實現 之 資料預處理
- 【python資料探勘課程】十四.Scipy呼叫curve_fit實現曲線擬合Python
- 機器學習 | 線性迴歸與邏輯迴歸機器學習邏輯迴歸
- Stanford機器學習課程筆記——單變數線性迴歸和梯度下降法機器學習筆記變數梯度
- 用線性迴歸無編碼實現文章瀏覽數預測
- 機器學習(二):理解線性迴歸與梯度下降並做簡單預測機器學習梯度
- 模式識別與機器學習——迴歸的線性模型模式機器學習模型
- 【機器學習】--線性迴歸從初識到應用機器學習
- 知否,知否,線性迴歸基礎教程值得擁有
- 資料探勘-預測模型彙總模型