正方形矩陣旋轉90度

將矩陣順時針旋轉90度。

---

方法一：

public static void rotate(int a[][],int N)
    {
        int layer;
        for(layer=0; layer<N/2; layer++)
        {
            int last = N-1-layer;
            for(int i=layer; i<last; i++)
            {
                int offset = i-layer;
                int top = a[layer][i];
                a[layer][i] = a[last-offset][layer];
                a[last-offset][layer] = a[last][last-offset];
                a[last][last-offset] = a[i][last];
                a[i][last] = top;
            }
        }
    }

程式碼的過程如圖所示：

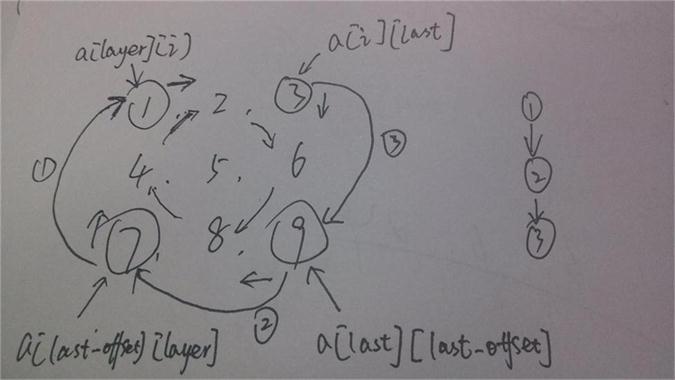
不用開闢新的空間。

方法二：

int[][] b = new int[N][N];
        for(int i=0;i<N;i++){
            for(int j=0;j<N;j++){
                b[N-1-j][N-1-i] = a[i][N-1-j];
            }
        }

第二種方法程式碼簡潔，但是需要開闢一個矩陣大小的空間。

當然我們推薦使用方法一。

---

矩陣乘法：

public int[][] multiMatrix(int[][] a , int[][] b)
    {
        int m = a.length;
        int n = b[0].length;
        int[][] result = new int[m][n];
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
            {
                int temp = 0;
                for (int k = 0; k < m; k++)
                {
                   temp += a[i][k]*b[k][j];
                }
                result[i][j] = temp;
            }
        return result;
    }