常見排序演算法小結

排序演算法經過了很長時間的演變，產生了很多種不同的方法。對於初學者來說，對它們進行整理便於理解記憶顯得很重要。每種演算法都有它特定的使用場合，很難通用。因此，我們很有必要對所有常見的排序演算法進行歸納。

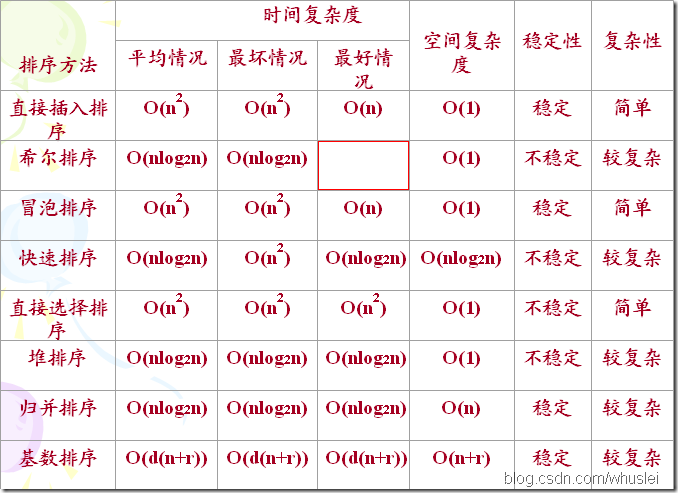
     我不喜歡死記硬背，我更偏向於弄清來龍去脈，理解性地記憶。比如下面這張圖，我們將圍繞這張圖來思考幾個問題。

     上面的這張圖來自一個PPT。它概括了資料結構中的所有常見的排序演算法。現在有以下幾個問題：

     1、每個演算法的思想是什麼？ 
     2、每個演算法的穩定性怎樣？時間複雜度是多少？ 
     3、在什麼情況下，演算法出現最好情況 or 最壞情況？ 
     4、每種演算法的具體實現又是怎樣的？

     這個是排序演算法裡面最基本，也是最常考的問題。下面是我的小結。

一、直接插入排序(插入排序)。

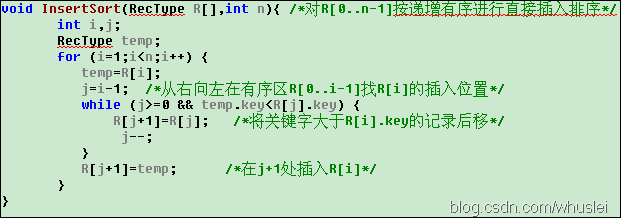
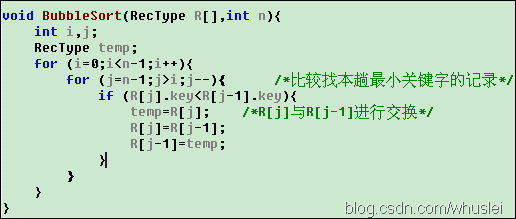
     1、演算法的虛擬碼(這樣便於理解)：    

     INSERTION-SORT (A, n)             A[1 . . n] 
     for j ←2 to n 
          do key ← A[ j] 
          i ← j – 1 
          while i > 0 and A[i] > key 
               do A[i+1] ← A[i] 
                    i ← i – 1 
          A[i+1] = key

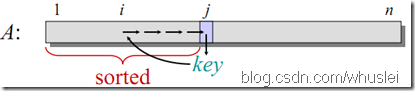
     2、思想：如下圖所示，每次選擇一個元素K插入到之前已排好序的部分A[1…i]中，插入過程中K依次由後向前與A[1…i]中的元素進行比較。若發現發現A[x]>=K,則將K插入到A[x]的後面，插入前需要移動元素。

     3、演算法時間複雜度。  
        最好的情況下：正序有序(從小到大)，這樣只需要比較n次，不需要移動。因此時間複雜度為O(n)  
        最壞的情況下：逆序有序,這樣每一個元素就需要比較n次，共有n個元素，因此實際複雜度為O(n^­2)  
        平均情況下：O(n^­2)

     4、穩定性。  
     理解性記憶比死記硬背要好。因此，我們來分析下。穩定性，就是有兩個相同的元素，排序先後的相對位置是否變化，主要用在排序時有多個排序規則的情況下。在插入排序中，K1是已排序部分中的元素，當K2和K1比較時，直接插到K1的後面(沒有必要插到K1的前面，這樣做還需要移動！！)，因此，插入排序是穩定的。

     5、程式碼(c版) blog.csdn.com/whuslei 
          

二、希爾排序(插入排序)

     1、思想：希爾排序也是一種插入排序方法,實際上是一種分組插入方法。先取定一個小於n的整數d1作為第一個增量,把表的全部記錄分成d1個組,所有距離為d1的倍數的記錄放在同一個組中,在各組內進行直接插入排序；然後,取第二個增量d2(＜d1),重複上述的分組和排序,直至所取的增量dt=1(dt<dt-1<…<d2<d1),即所有記錄放在同一組中進行直接插入排序為止。    

     例如：將 n 個記錄分成 d 個子序列： 
       { R[0]，   R[d]，     R[2d]，…，     R[kd] } 
       { R[1]，   R[1+d]， R[1+2d]，…，R[1+kd] } 
         … 
       { R[d-1]，R[2d-1]，R[3d-1]，…，R[(k+1)d-1] }

      
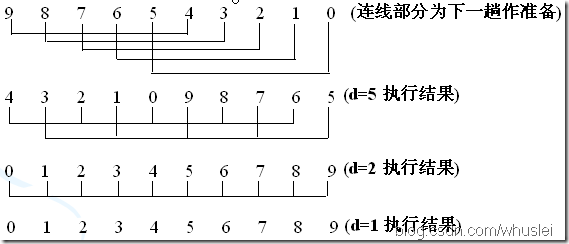
     說明：d=5 時，先從A[d]開始向前插入，判斷A[d-d]，然後A[d+1]與A[(d+1)-d]比較，如此類推，這一回合後將原序列分為d個組。<由後向前>

     2、時間複雜度。  
     最好情況：由於希爾排序的好壞和步長d的選擇有很多關係，因此，目前還沒有得出最好的步長如何選擇(現在有些比較好的選擇了，但不確定是否是最好的)。所以，不知道最好的情況下的演算法時間複雜度。  
     最壞情況下：O(N*logN)，最壞的情況下和平均情況下差不多。  
     平均情況下：O(N*logN)

     3、穩定性。  
     由於多次插入排序，我們知道一次插入排序是穩定的，不會改變相同元素的相對順序，但在不同的插入排序過程中，相同的元素可能在各自的插入排序中移動，最後其穩定性就會被打亂，所以shell排序是不穩定的。(有個猜測，方便記憶：一般來說，若存在不相鄰元素間交換，則很可能是不穩定的排序。)

     4、程式碼(c版) blog.csdn.com/whuslei 
           

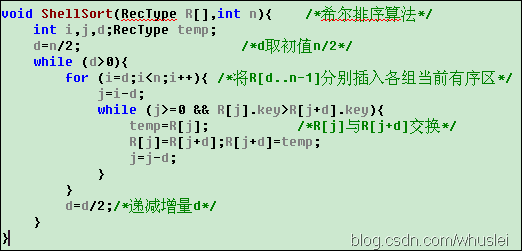
三、氣泡排序(交換排序)

       1、基本思想：通過無序區中相鄰記錄關鍵字間的比較和位置的交換,使關鍵字最小的記錄如氣泡一般逐漸往上“漂浮”直至“水面”。 
             2、時間複雜度  
     最好情況下：正序有序，則只需要比較n次。故，為O(n)  
      最壞情況下:  逆序有序，則需要比較(n-1)+(n-2)+……+1，故，為O(N*N)

      3、穩定性  
      排序過程中只交換相鄰兩個元素的位置。因此，當兩個數相等時，是沒必要交換兩個數的位置的。所以，它們的相對位置並沒有改變，氣泡排序演算法是穩定的！

      4、程式碼(c版) blog.csdn.com/whuslei 
          

四、快速排序(交換排序)

     1、思想：它是由氣泡排序改進而來的。在待排序的n個記錄中任取一個記錄(通常取第一個記錄),把該記錄放入適當位置後,資料序列被此記錄劃分成兩部分。所有關鍵字比該記錄關鍵字小的記錄放置在前一部分,所有比它大的記錄放置在後一部分,並把該記錄排在這兩部分的中間(稱為該記錄歸位),這個過程稱作一趟快速排序。

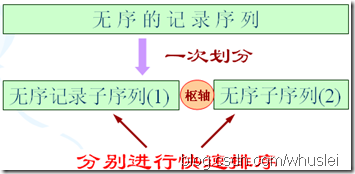           說明：最核心的思想是將小的部分放在左邊，大的部分放到右邊，實現分割。         
     2、演算法複雜度  
      最好的情況下：因為每次都將序列分為兩個部分(一般二分都複雜度都和logN相關)，故為 O(N*logN)  
      最壞的情況下：基本有序時，退化為氣泡排序，幾乎要比較N*N次，故為O(N*N)

      3、穩定性  
      由於每次都需要和中軸元素交換，因此原來的順序就可能被打亂。如序列為 5 3 3 4 3 8 9 10 11會將3的順序打亂。所以說，快速排序是不穩定的！

      4、程式碼(c版) 
           

五、直接選擇排序(選擇排序)

      1、思想：首先在未排序序列中找到最小元素，存放到排序序列的起始位置，然後，再從剩餘未排序元素中繼續尋找最小元素，然後放到排序序列末尾。以此類推，直到所有元素均排序完畢。具體做法是：選擇最小的元素與未排序部分的首部交換，使得序列的前面為有序。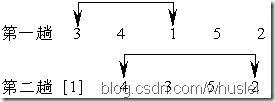  
      2、時間複雜度。 
      最好情況下：交換0次，但是每次都要找到最小的元素，因此大約必須遍歷N*N次，因此為O(N*N)。減少了交換次數！ 
      最壞情況下，平均情況下：O(N*N)

      3、穩定性 
      由於每次都是選取未排序序列A中的最小元素x與A中的第一個元素交換，因此跨距離了，很可能破壞了元素間的相對位置，因此選擇排序是不穩定的！

      4、程式碼(c版)blog.csdn.com/whuslei 
          

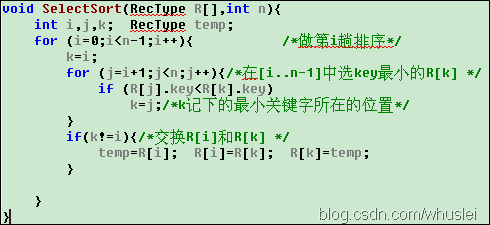
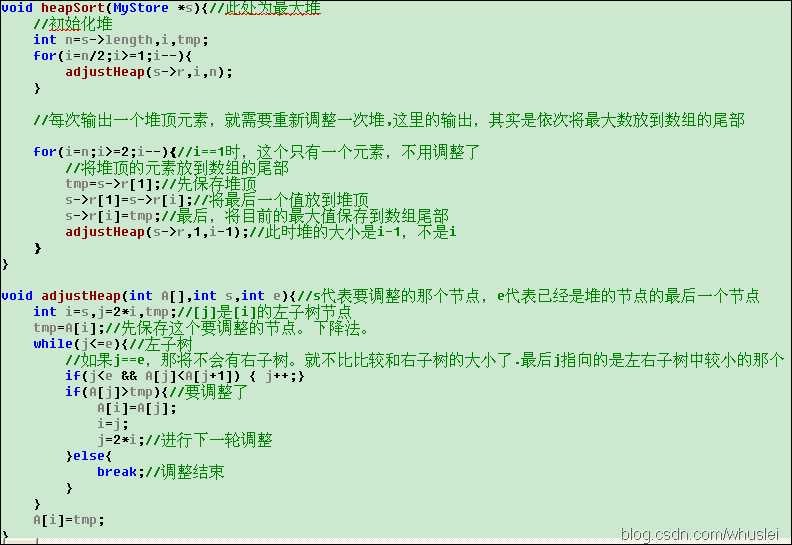
六、堆排序

     1、思想：利用完全二叉樹中雙親節點和孩子節點之間的內在關係，在當前無序區中選擇關鍵字最大(或者最小)的記錄。也就是說，以最小堆為例，根節點為最小元素，較大的節點偏向於分佈在堆底附近。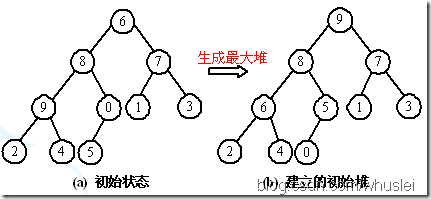 
      2、演算法複雜度 
         最壞情況下，接近於最差情況下：O(N*logN)，因此它是一種效果不錯的排序演算法。

      3、穩定性 
         堆排序需要不斷地調整堆，因此它是一種不穩定的排序！

      4、程式碼(c版，看程式碼後更容易理解！)      
          

七、歸併排序

      1、思想：多次將兩個或兩個以上的有序表合併成一個新的有序表。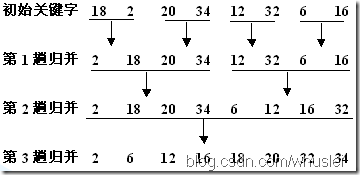 
       2、演算法時間複雜度 
          最好的情況下：一趟歸併需要n次，總共需要logN次，因此為O(N*logN) 
          最壞的情況下，接近於平均情況下，為O(N*logN) 
          說明：對長度為n的檔案，需進行logN 趟二路歸併，每趟歸併的時間為O(n)，故其時間複雜度無論是在最好情況下還是在最壞情況下均是O(nlgn)。

      3、穩定性 
         歸併排序最大的特色就是它是一種穩定的排序演算法。歸併過程中是不會改變元素的相對位置的。 
      4、缺點是，它需要O(n)的額外空間。但是很適合於多連結串列排序。 
      5、程式碼(略)blog.csdn.com/whuslei

八、基數排序

      1、思想：它是一種非比較排序。它是根據位的高低進行排序的，也就是先按個位排序，然後依據十位排序……以此類推。示例如下：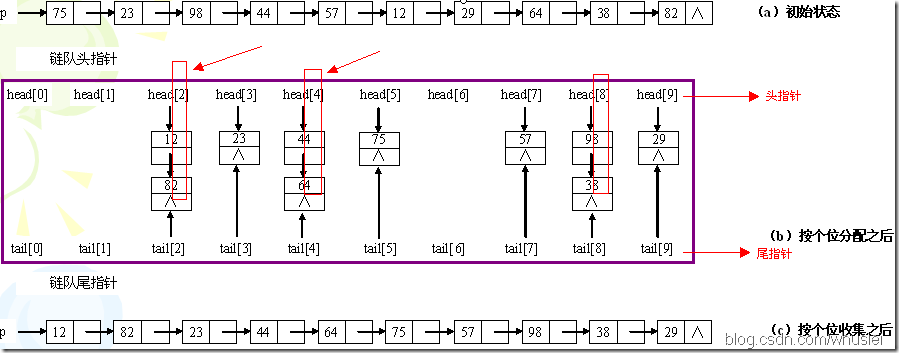 

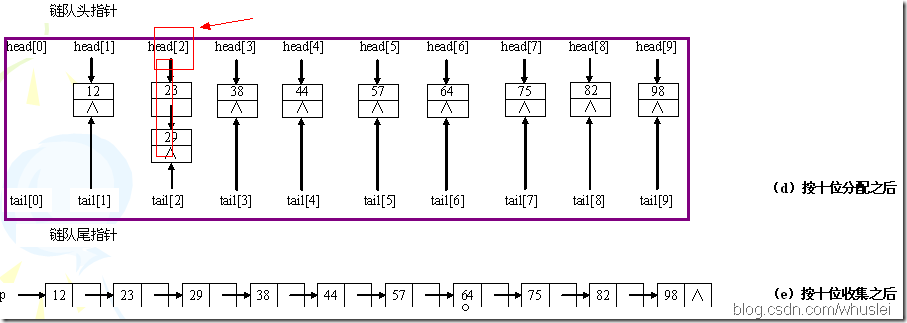        2、演算法的時間複雜度 
       分配需要O(n),收集為O(r),其中r為分配後連結串列的個數，以r=10為例，則有0～9這樣10個連結串列來將原來的序列分類。而d，也就是位數(如最大的數是1234，位數是4，則d=4)，即"分配-收集"的趟數。因此時間複雜度為O(d*(n+r))。

       3、穩定性 
          基數排序過程中不改變元素的相對位置，因此是穩定的！

       4、適用情況：如果有一個序列，知道數的範圍(比如1～1000)，用快速排序或者堆排序，需要O(N*logN)，但是如果採用基數排序，則可以達到O(4*(n+10))=O(n)的時間複雜度。算是這種情況下排序最快的！！

       5、程式碼(略)

     總結： 每種演算法都要它適用的條件，本文也僅僅是回顧了下基礎。如有不懂的地方請參考課本。 

原文地址：http://blog.csdn.net/whuslei/article/details/6442755?locationNum=2&fps=1