樹形結構的資料在專案開發中比較常見,比如比較典型的是論壇主題留言。
每一個主題(節點)可以有n個留言(子節點)。這些留言又可以有自己的留言。因此這種結構就是一顆樹。本文討論的是資料庫中如何儲存這種樹形結構。
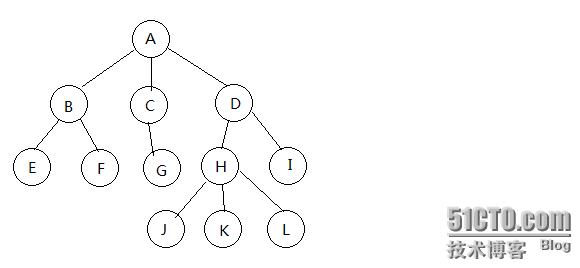
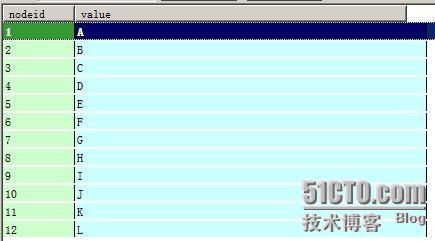
假設有如下一棵樹:
方法一
注意:本例中的資料庫是SQLite,因此SQL語句只對SQLite有效,其他資料庫可以參考該寫法。
要儲存於資料庫中,最簡單直接的方法,就是儲存每個元素的父節點ID。
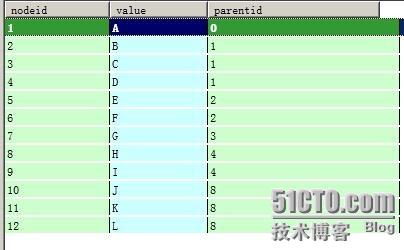
暫且把這種方法命名依賴父節點法,因此表結構設計如下:
儲存的資料如下格式:
這種結構下,如果查詢某一個節點的直接子節點,十分容易,比如要查詢D節點的子節點。
|
1
|
select * from tree1 where parentid=4
|
如果要插入某個節點,比如在D節點下,再次插入一個M節點。
只需要如下SQL:
|
1
|
INSERT INTO tree1 (value,parentid) VALUES('M',4);
|
這種結構在查詢某個節點的所有子節點,就稍顯複雜,無論是SELECT還是DELETE都可能涉及到獲取所有子節點的問題。比如要刪除一個節點並且該節點的子節點也要全部刪除,那麼首先要獲得所有子節點的ID,因為子節點並不只是直接子節點,還可能包含子節點的子節點。比如刪除D節點及其子節點,必須先查出D節點下的所有子節點,然後再做刪除,SQL如下:
|
1
2
3
4
|
select nodeid from tree1 where parentid=4 --返回8,9
select nodeid from tree1 where parentid in (8,9) --返回10,11,12
select nodeid from tree1 where parentid in (10,11,12) --返回空
delete from tree1 where nodeid in (4,8,9,10,11,12)
|
如果是隻刪除D節點,對於其它節點不做刪除而是做提升,那麼必須先修改子節點的parentid,然後才能刪除D節點。
正如上面演示的,對於這種依賴父節點法,最大的缺點就是無法直接獲得某個節點的所有子節點。因此如果要select所有的子節點,需要繁瑣的步驟,這不利於做聚合操作。
對於某些資料庫產品,支援遞迴查詢語句的,比如微軟的SQL Server,可以使用CTE技術實現遞迴查詢。比如,要查詢D節點的所有子節點。只需要如下語句:
|
1
2
3
4
5
6
|
WITH tmp AS(
SELECT * FROM Tree1 WHERE nodeid = 4
UNION ALL
SELECT a.* FROM Tree1 AS a,tmp AS b WHERE a.parentid = b. nodeid
)SELECT * FROM tmp
|
但是對於那些不支援遞迴查詢的資料庫來說,實現起來就比較複雜了。
方法二
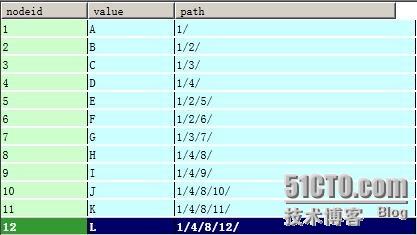
還有一種比較土的方法,就是儲存路徑。暫且命名為路徑列舉法。
這種方法,將儲存根結點到每個節點的路徑。
這種資料結構,可以一眼就看出子節點的深度。
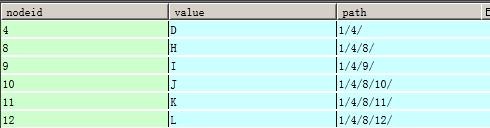
如果要查詢某個節點下的子節點,只需要根據path的路徑去匹配,比如要查詢D節點下的所有子節點。
|
1
|
select * from tree2 where path like '%/4/%'
|
或者出於效率考慮,直接寫成
|
1
|
select * from tree2 where path like '1/4/%'
|
如果要做聚合操作,也很容易,比如查詢D節點下一共有多少個節點。
select count(*) from tree2 where path like '1/4/%';
要插入一個節點,則稍微麻煩點。要插入自己,然後查出父節點的Path,並且把自己生成的ID更新到path中去。比如,要在L節點後面插入M節點。
首先插入自己M,然後得到一個nodeid比如nodeid=13,然後M要插入到L後面,因此,查出L的path為1/4/8/12/,因此update M的path為1/4/8/12/13
|
1
2
3
4
5
|
update tree2 set
path=(select path from tree2 where nodeid=12) --此處開始拼接
||last_insert_rowid()||'/'
wherenodeid= last_insert_rowid(); |
這種方法有一個明顯的缺點就是path欄位的長度是有限的,這意味著,不能無限制的增加節點深度。因此這種方法適用於儲存小型的樹結構。
方法三
下面介紹一種方法,稱之為閉包表。
該方法記錄了樹中所有節點的關係,不僅僅只是直接父子關係,它需要使用2張表,除了節點表本身之外,還需要使用1張表來儲存節祖先點和後代節點之間的關係(同時增加一行節點指向自身),並且根據需要,可以增加一個欄位,表示深度。因此這種方法資料量很多。設計的表結構如下:
Tree3表:
NodeRelation表:
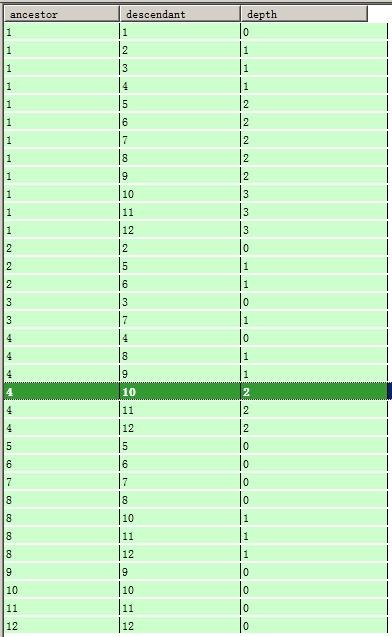
如例子中的樹,插入的資料如下:
Tree3表的資料
NodeRelation表的資料
可以看到,NodeRelation表的資料量很多。但是查詢非常方便。比如,要查詢D節點的子元素
只需要
|
1
|
select * from NodeRelation where ancestor=4;
|
要查詢節點D的直接子節點,則加上depth=1
|
1
|
select * from NodeRelation where ancestor=4 and depth=1;
|
要查詢節點J的所有父節點,SQL:
|
1
|
select * from NodeRelation where descendant=10;
|
如果是插入一個新的節點,比如在L節點後新增子節點M,則插入的節點除了M自身外,還有對應的節點關係。即還有哪些節點和新插入的M節點有後代關係。這個其實很簡單,只要和L節點有後代關係的,和M節點必定會有後代關係,並且和L節點深度為X的和M節點的深度必定為X+1。因此,在插入M節點後,找出L節點為後代的那些節點作為和M節點之間有後代關係,插入到資料表。
|
1
2
3
4
5
6
7
|
INSERT INTO tree3 (value) VALUES('M');--插入節點
INSERT INTO NodeRelation(ancestor,descendant,depth)
select n.ancestor,last_insert_rowid(),n.depth+1--此處深度+1作為和M節點的深度
from NodeRelation n
where n.descendant=12
Union ALL
select last_insert_rowid() ,last_insert_rowid(),0 --加上自身
|
在某些並不需要使用深度的情況下,甚至可以不需要depth欄位。
如果要刪除某個節點也很容易,比如,要刪除節點D,這種情況下,除了刪除tree3表中的D節點外,還需要刪除NodeRelation表中的關係。
首先以D節點為後代的關係要刪除,同時以D節點的後代為後代的這些關係也要刪除:
|
1
2
|
delete from NodeRelation where descendant in
(select descendant from NodeRelation where ancestor=4 );--查詢以D節點為祖先的那些節點,即D節點的後代。
|
這種刪除方法,雖然徹底,但是它也刪除了D節點和它原本的子節點的關係。
如果只是想割裂D節點和A節點的關係,而對於它原有的子節點的關係予以保留,則需要加入限定條件。
限制要刪除的關係的祖先不以D為祖先,即如果這個關係以D為祖先的,則不用刪除。因此把上面的SQL加上條件。
|
1
2
3
|
delete from NodeRelation where descendant in
(select descendant from NodeRelation where ancestor=4 );--查詢以D節點為祖先的那些節點,即D節點的後代。
and ancestor not in (select descendant from NodeRelation where ancestor =4 )
|
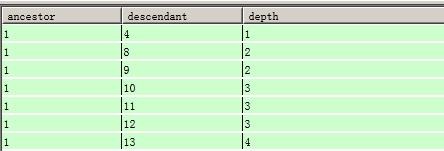
上面的SQL用文字描述就是,查詢出D節點的後代,如果一個關係的祖先不屬於D節點的後代,並且這個關係的後代屬於D節點的後代,就刪除它。
這樣的刪除,保留了D節點自身子節點的關係,如上面的例子,實際上刪除的節點關係為:
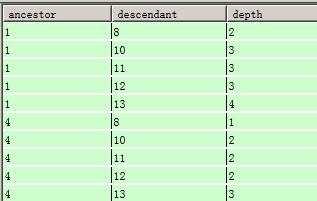
如果要刪除節點H,則為
總結:
上面主要講了3種方式,各有優點缺點。可以根據實際需要,選擇合適的資料模型。