文字生成(Text Generation)通過 機器學習 + 自然語言處理 技術嘗試使AI具有人類水平的語言表達能力,從一定程度上能夠反應現今自然語言處理的發展水平。
下面用極簡的描述介紹一下文字生成技術的大體框架,具體可以參閱各種網路文獻(比如:CSDN經典Blog“好玩的文字生成”[1]),論文等。
文字生成按任務來說,比較流行的有:機器翻譯、句子生成、對話生成等,本文著重討論後面兩種。
基於深度學習的Text Generator 通常使用迴圈神經網路(Basic RNN,LSTM,GRU等)進行語義建模。
在句子生成任務中,一種常見的應用:“Char-RNN”(這裡“Char”是廣義上的稱謂,可以泛指一個字元、單詞或其他文字粒度單位),雖然簡單基礎但可以清晰度反應句子生成的執行流程,
首先需要建立一個詞庫Vocab包含可能出現的所有字元或是詞彙,每次模型將預測得到句子中下一個將出現的詞彙,要知道softmax輸出的只是一個概率分佈,其維度為詞庫Vocab 的size,
需再通過函式將輸出概率分佈轉化為 One-hot vector,從詞庫 Vocab 中檢索得出對應的詞項;
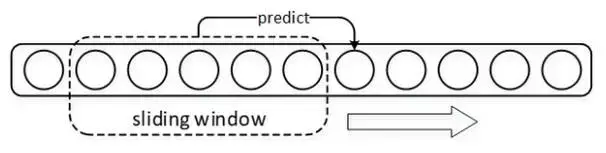
在“Char-RNN”模型訓練時,使用視窗在語料上滑動,視窗之內的上下文及其後緊跟的字元配合分別為一組訓練樣本和標籤,每次以按照固定的步長滑動視窗以得出全部 “樣本-標籤” 對。
與句子生成任務類似,對話生成以每組Dialogue作為 “樣本-標籤” 對,迴圈神經網路RNN_1對Dialogue上文進行編碼,再用另一個迴圈神經網路RNN_2對其進行逐詞解碼,並以上一個解碼神經元的輸出作為下一個解碼神經元的輸入,生成Dialogue下文,
需要注意的是:在解碼前需配置“開始”標記 _,用於指示解碼器Decoder開啟Dialogue下文首詞(or 字)的生成,並配置“結束”標記 _,用於指示解碼器結束當前的 Text Generation 程式。
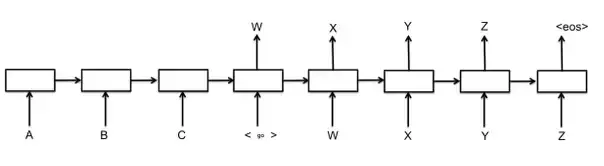
這便是眾所周知的“Seq2Seq”框架的基礎形態,為了提高基礎Seq2Seq模型的效果,直接從解碼器的角度有諸如 Beam-SearchDecoder[2]、Attention mechanismDecoder[3](配置注意力機制的解碼器)等改進,而從神經網路的結構入手,也有諸如Pyramidal RNN[4](金字塔型RNN)、Hierarchical RNN Encoder[5](分層迴圈網路編碼器)等改進。
改進不計其數,不一一詳舉,但不管如何,預測結果的輸出始終都是一個維度為詞庫大小的概率分佈,需要再甄選出最大值的Index,到詞庫Vocab中檢索得出對應的單詞(or 字元)。
2.1GAN基礎知識
GAN對於大家而言想必已經膾炙人口了,這裡做一些簡單的複習。
GAN從結構上來講巧妙而簡單(儘管有與其他經典工作Idea相似的爭議[6~7]),也非常易於理解,整個模型只有兩個部件:1.生成器G;2.判別器D。
生成模型其實由來已久,所以生成器也並不新鮮,生成器G的目標是生成出最接近於真實樣本的假樣本分佈,在以前沒有判別器D的時候,生成器的訓練依靠每輪迭代返回當前生成樣本與真實樣本的差異(把這個差異轉化成loss)來進行引數優化,而判別器D的出現改變了這一點,判別器D的目標是儘可能準確地辨別生成樣本和真實樣本,而這時生成器G的訓練目標就由最小化“生成-真實樣本差異”變為了儘量弱化判別器D的辨別能力(這時候訓練的目標函式中包含了判別器D的輸出)。
GAN模型的大體框架如下圖所示:
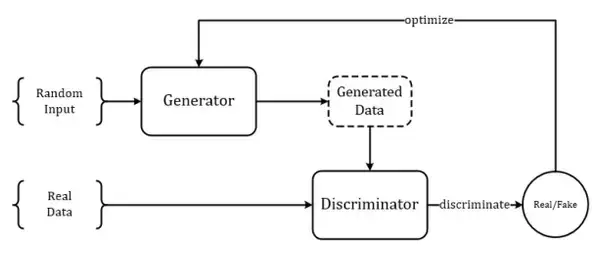
我們再來簡單複習一下GAN當中的一些重要公式,這一步對後文的闡述非常重要。
不管生成器G是什麼形狀、多麼深的一個神經網路,我們暫且把它看成一個函式 G(\cdot) ,由它生成的樣本記作: p_g(x) ,相對地,真實樣本記作: p_{data}(x) 。
同樣,不管判別器D作為一個分類神經網路,我們也可將其視為一個函式 D(\cdot) ,而這個函式的輸出即為一個標量,用於描述生成樣本 p_g(x) 與真實樣本 p_{data}(x) 之間的差距。
而GAN模型的整體優化目標函式是:
\arg\min_{G}\max_{D}=V(G,D)
其中函式 V(G,D) 如下:
V=\mathbb{E}_{x \sim p_{data}}[\log D(x)] + \mathbb{E}_{x \sim p_g}[\log (1-D(x))]
根據連續函式的期望計算方法,上式變形為:
V=\int_{x}\left[ p_{data}(x) \log D(x) + p_g(x) log(1-D(x))\right]
先求外層的 \arg\max_{D}V(G,D) 的話,對積分符號內的多項式求導取極值得到目標D:
D^*(x)=\frac{p_{data}(x)}{p_{data}(x) + p_g(x)}
代回原式:
\begin{aligned} V(G,D^*) &= \int_x p_{data}(x)\log \frac{p_{data}(x)}{p_{data}(x) + p_g(x)} + \int_x p_g \log \frac{p_g(x)}{p_{data}(x) + p_g(x)}\\ &= -\log 4+ KL\left( p_{data}(x) \Arrowvert \frac{p_{data}(x) + p_g(x)}{2} \right) + KL\left( p_g(x) \Arrowvert \frac{p_{data}(x) + p_g(x)}{2} \right)\\ &= -\log 4 + 2\cdot JSD(p_{data}(x) \Arrowvert p_g(x)) \end{aligned}
所以,當生成器G能生成出與真實樣本一樣分佈的樣本,那麼ok,就達到最好的結果,然後大家注意一點,這裡生成樣本的loss衡量方法是JS散度。
2.2GAN面對離散型資料時的困境(啥是離散型資料?)
GAN的作者早在原版論文[8]時就提及,GAN只適用於連續型資料的生成,對於離散型資料效果不佳(使得一時風頭無兩的GAN在NLP領域一直無法超越生成模型的另一大佬VAE[9])。
文字資料就是最典型的一種離散型資料,這裡所謂的離散,並不是指:文字由一個詞一個片語成,或是說當今最流行的文字生成框架,諸如Seq2Seq,也都是逐詞(或者逐個Character)生成的。
因為哪怕利用非迴圈網路進行一次成型的Sentences生成,也無法避免“資料離散”帶來的後果,抱歉都怪我年輕時的無知,離散型資料的真正含義,我們要從連續性資料說起。
影像資料就是典型的連續性資料,故而GAN能夠直接生成出逼真的畫面來。我們首先來看看影像資料的形狀:
影像資料在計算機中均被表示為矩陣,若是黑白影像矩陣中元素的值即為畫素值或者灰度值(抱歉外行了,我不是做影像的),就算是彩色影像,影像張量即被多加了一階用於表示RGB通道,影像矩陣中的元素是可微分的,其數值直接反映出影像本身的明暗,色彩等因素,很多這樣的畫素點組合在一起,就形成了影像,也就是說,從影像矩陣到影像,不需要“取樣”(Sampling),
有一個更形象的例子:畫圖軟體中的調色盤,如下圖,你在調色盤上隨便滑動一下,大致感受一下影像資料可微分的特性。
文字資料可就不一樣了,做文字的同學都知道,假設我們的詞庫(Vocabulary)大小為1000,那麼每當我們預測下一個出現的詞時,理應得到的是一個One-hot的Vector,這個Vector中有999項是0,只有一項是1,而這一項就代表詞庫中的某個詞。然而,真正的隔閡在於,我們每次用無論什麼分類器或者神經網路得到的直接結果,都是一個1000維的概率分佈,而非正正好好是一個One-hot的Vector,即便是使用softmax作為輸出,頂多也只能得到某一維上特別大,其餘維上特別小的情況,而將這種輸出結果過渡到One-hot vector 然後再從詞庫中查詢出對應index的詞,這樣的操作被稱為“Sampling”,通常,我們找出值最大的那一項設其為1,其餘為0。
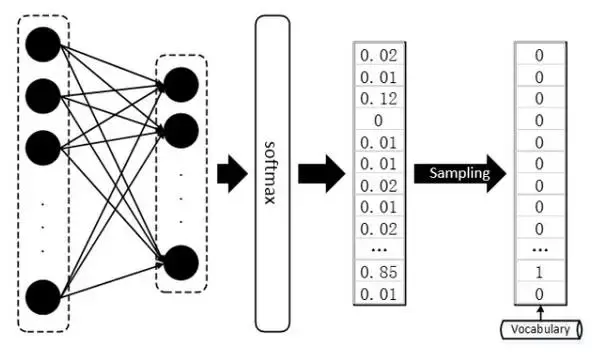
當前神經網路的優化方法大多數都是基於梯度的(Gradient based),很多文獻這麼說:GAN在面對離散型資料時,判別網路無法將梯度Back propagation(BP)給生成網路。這句話當時讓我等聽的雲裡霧裡,不妨換一個角度理解,我們知道,基於梯度的優化方法大致意思是這樣的,微調網路中的引數(weight),看看最終輸出的結果有沒有變得好一點,有沒有達到最好的情形。
但是判別器D得到的是Sampling之後的結果,也就是說,我們經過引數微調之後,即便softmax的輸出優化了一點點,比如上圖的例子中,正確結果本應是第三項,其output的倒數第二項從 0.85 變為了 0.65 ,第三項從 0.12 變為了 0.32 ,但是經過Sampling之後,生成器G輸出的結果還是跟以前一模一樣,並再次將相同的答案重複輸入給判別器D,這樣判別器D給出的評價就會毫無意義,生成器G的訓練也會失去方向。
有人說,與其這樣不如每次給判別器D直接吃Sampling之前的結果,也就是softamx輸出的那個distribution,同樣,這麼做也有很大的問題。我們回到GAN的基本原理,判別器D的初衷,它經歷訓練就是為了準確辨別生成樣本和真實樣本的,那麼生成樣本是一個充滿了float小數的分佈,而真實樣本是一個One-hot Vector,判別器D很容易“作弊”,它根本不用去判斷生成分佈是否與真實分佈更加接近,它只需要識別出給到的分佈是不是除了一項是 1 ,其餘都是 0 就可以了。所以無論Sampling之前的分佈無論多麼接近於真實的One-hot Vector,只要它依然是一個概率分佈,都可以被判別器D輕易地檢測出來。
上面所說的原因當然也有數學上的解釋,還記得在2.1節的時候,請大家注意生成樣本的loss衡量標準是什麼嗎?沒錯,就是JS散度, JS-divergence 在應用上其實是有弱點的(參考文獻[10]),它只能被正常地應用於互有重疊(Overlap)的兩個分佈,當面對互不重疊的兩個分佈 P 和 Q ,其JS散度:
JSD(P \Arrowvert Q) \equiv \log{2}
大家再想想,除非softmax能output出與真實樣本 exactly 相同的獨熱分佈(One-hot Vector)(當然這是不可能的),還有什麼能讓生成樣本的分佈與真實樣本的分佈發生重疊呢?於是,生成器無論怎麼做基於Gradient 的優化,輸出分佈與真實分佈的 JSD(p_{data} \Arrowvert p_g) 始終是 \log{2} ,生成器G的訓練於是失去了意義。
為了解決GAN在面對離散資料時的困境,最直接的想法是對GAN內部的一些計算方式進行微調,這種對於GAN內部計算方式的直接改進也顯示出了一定的效果,為後面將GAN直接、流暢地應用於文字等離散型資料的生成帶來了希望。 接下來簡單介紹相關的兩篇工作[11~12]。
3.1Wasserstein-divergence,額外的禮物
Wasserstein GAN[13](簡稱WGAN),其影響力似乎達到了原版GAN的高度,在國內也有一篇與其影響力相當的博文——“令人拍案叫絕的Wasserstein GAN”[10],不過在看這篇論文之前,還要推薦另外一篇論文“f-GAN”[14],這篇論文利用芬切爾共軛(Fenchel Conjugate)的性質證明了任何 f-Divergence 都可以作為原先GAN中 KL-Divergence (或者說 JS-Divergence )的替代方案。 f-GAN 的定義如下:
D_f(P \Arrowvert Q) = \int_{x} q(x) f\left( \frac{p(x)}{q(x)} \right) dx
公式中的 f(\cdot) 被稱為 f函式,它必須滿足以下要求:
\left\{ \begin{aligned} & f \ is \ convex \quad (凸函式) \\ & f(1) = 0 \end{aligned} \right.
不難看出, KL-Divergence 也是 f-Divergence 的一種,f-GAN 原文提供了數十種各式各樣的 f-Divergence ,為GAN接下來沿此方向上的改進帶來了無限可能。
Wasserstein GAN 對GAN的改進也是從替換 KL-Divergence 這個角度對GAN進行改進,其詳細的妙處大可參看文獻[10,13],總的來說,WGAN採用了一種奇特的 Divergence—— “推土機-Divergence”, Wasserstein-Divergence 將兩個分佈看作兩堆土,Divergence 計算的就是為了將兩個土堆推成一樣的形狀所需要泥土搬運總距離。如下圖:
使用 Wasserstein-Divergence 訓練的GAN相比原版的GAN有更加明顯的“演化”過程,換句話說就是,WGAN的訓練相比與GAN更加能突顯從“不好”到“不錯”的循序漸經的過程。
從上面的2.2節,我們知道JS散度在面對兩個分佈不相重疊的情況時,將發生“異常”,計算結果均為 \log{2} ,GAN的訓練過程也是這樣,也許在很長一段訓練的過程中,JS散度的返回值都是 \log{2} ,只有到達某個臨界點時,才會突然優化為接近最優值的結果,而Wasserstein散度的返回值則要平滑很多。
既然Wasserstein散度能夠克服JS散度的上述弱點,那麼使用Wasserstein GAN直接吸收生成器G softmax層output的Distribution Vector 與真實樣本的 One-hot Vector,用判別器D 進行鑑定,即便判別器D不會傻到真的被“以假亂真”,但生成器output每次更加接近於真實樣本的“進步”總算還是能被傳回,這樣就保證了對於離散資料的對抗訓練能夠繼續下去。 不過Wasserstein GAN的原著放眼於對於GAN更加遠大的改進意義,並沒有著重給出關於文字生成等離散資料處理的實驗,反倒是後來的一篇“Improved Training of Wasserstein GANs”[11]專門給出了文字生成的實驗,從結果上可以看出,WGAN生成的文字雖然遠不及當下最牛X的文字生成效果,但好歹能以character為單位生成出一些看上去稍微正常一點的結果了,對比之下,GAN關於文字生成的生成結果顯然是崩塌的。

3.2Gumbel-softmax,模擬Sampling的softmax
另外一篇來自華威大學+劍橋大學的工作把改進GAN用於離散資料生成的重心放在了修改softmax的output這方面。如2.2節所述,Sampling 操作中的 \arg\max(\cdot) 函式將連續的softmax輸出抽取成離散的成型輸出,從而導致Sampling的最終output是不可微的,形成GAN對於離散資料生成的最大攔路虎,既然不用Sampling的時候,output與真實分佈不重疊,導致JS散度停留於固定值 \log{2} ,如果用了Sampling的話,離散資料的正常輸出又造成了梯度 Back-Propagation 上天然的隔閡。
既然如此,論文的作者尋找了一種可以高仿出Sampling效果的特殊softmax,使得softmax的直接輸出既可以保證與真實分佈的重疊,又能避免Sampling操作對於其可微特徵的破壞。它就是“耿貝爾-softmax”(Gumbel-Softmax),Gumbel-Softmax早先已經被應用於離散標籤的再分佈化[15](Categorical Reparameterization),在原先的Sampling操作中, \arg\max(\cdot) 函式將普通softmax的輸出轉化成One-hot Vector:
\mathrm{y} = one\_hot\left( \arg\max \left( softmax(\mathrm{h}) \right) \right)
而Gumbel-Softmax略去了 one\_hot(\cdot) + \arg\max(\cdot) 這一步,能夠直接給出近似Sampling操作的輸出:
\mathrm{y} = softmax \left( 1 / \tau (\mathrm{h} + \mathrm{g}) \right)
精髓在於這其中的“逆溫引數” \tau ,當 \tau \longrightarrow 0 時,上式所輸出的分佈等同於 one\_hot(\cdot) + \arg\max(\cdot) 給出的 Sampling 分佈,而當 \tau \longrightarrow \infty 時,上式的輸出就接近於均勻分佈,而 \tau 則作為這個特殊softmax中的一個超引數,給予一個較大的初始值,通過訓練學習逐漸變小,向 0 逼近,這一部分詳細內容可以閱讀文獻[15]。
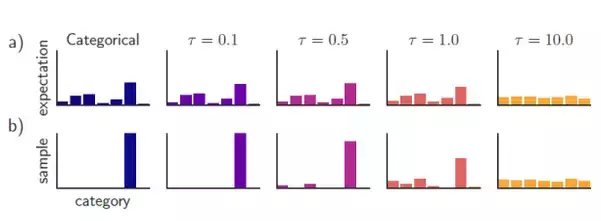
論文的實驗僅僅嘗試使用配合Gumbel-Softmax的GAN進行長度固定為12的 Context-free grammar 序列生成,可見GAN的訓練並沒有崩塌,在少數樣例上也得到了還算逼真的效果。

所以,對於GAN進行直接改進用於文字生成,雖說是取得了一定的成效,但距離理想的狀態仍然道阻且長,有沒有更好的辦法呢?當然!
4.1關於Reinforcement Learning的閒聊閒扯
強化學習(Reinforcement Learning,RL)由於其前衛的學習方式,本不如監督學習那麼方便被全自動化地實現,並且在很多現實應用中學習週期太長,一直沒有成為萬眾矚目的焦點,直到圍棋狗的出現,才吸引了眾多人的眼球。
RL通常是一個馬爾科夫決策過程,在各個狀態 s_i 下執行某個動作 x_i 都將獲得獎勵(或者是"負獎勵"——懲罰) Reward(s_i, x_i) ,而將從頭到尾所有的動作連在一起就稱為一個“策略”或“策略路徑” \theta^\pi ,強化學習的目標就是找出能夠獲得最多獎勵的最優策略:
為了達到這個目標,強化學習機可以在各個狀態嘗試各種可能的動作,並通過環境(大多數是人類)反饋的獎勵或者懲罰,評估並找出能夠最大化 期望獎勵
的策略。
其實也有人將RL應用於對話生成的訓練當中[16],因為對話生成任務本身非常符合強化學習的執行機理(讓人類滿意,拿獎勵)。設,根據輸入句子 a ,返回的回答 x 從人類得到的獎勵記為 R(a,x) ,而Encoder-Decoder對話模型服從的引數被統一記為 \theta ,則基於RL的目標函式說白了就是最大化生成對話的期望獎勵,其中 P_{\theta}\left( a, x \right) 表示在引數 \theta 下,一組對話 (a, x) 出現的概率。
既然是一個最優化的問題,很直接地便想到使用基於梯度(Gradient)的優化方法解決。當然,在強化學習中,我們要得到的是最優策略 \theta_{best} ,此過程便在強化學習領域常聽到的 Policy Gradient。我們把等式右邊 \arg \max \limits_{\theta}(\cdot) 中的項單獨記為 \tilde{R_{\theta}} ,它表示對話模型找到最優引數時所得到的獎勵期望。在實做時,設某句話的應答有$N$種可能性,則每組對話 (a^i, x^i) 出現的概率可視為服從均勻分佈,故還可以進行如下變形:
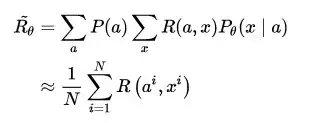
在優化過程中,對話模型的權重 \theta 更新如下, \nabla \tilde{R_{\theta}} 為所獲獎勵的變化梯度,
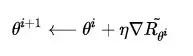
藉助複合函式的求導法則,繼續推導獎勵的變化梯度,
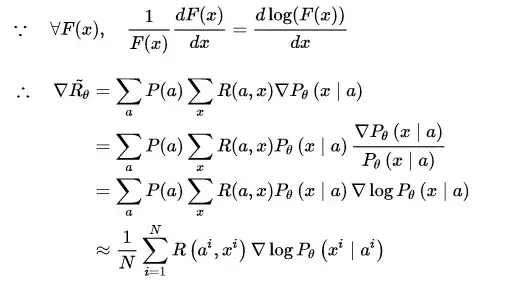
這樣一來,梯度優化的重心就轉化到了生成對話的概率上來,也就是說,通過對引數 \theta 進行更新,獎勵會使模型趨於將優質對話的出現概率提高,而懲罰則會讓模型趨於將劣質對話的出現概率降低。
自AlphaGo使得強化學習猛然進入大眾視野以來,大部分對於強化學習的理論研究都將遊戲作為主要實驗平臺,這一點不無道理,強化學習理論上的推導看似邏輯通順,但其最大的弱點在於,基於人工評判的獎勵 Reward 的獲得,讓實驗人員守在電腦前對模型吐出來的結果不停地打分看來是不現實的,遊戲系統恰恰能會給出正確客觀的打分(輸/贏 或 遊戲Score)。基於RL的對話生成同樣會面對這個問題,研究人員採用了類似AlphaGo的實現方式(AI棋手對弈)——同時執行兩個機器人,讓它們自己互相對話,同時,使用預訓練(pre-trained)好的“打分器”給出每組對話的獎勵得分 R(a^i, x^i) ,關於這個預訓練的“打分器” R ,可以根據實際的應用和需求自己DIY。 R(a^i, x^i) = \lambda_1 R(是否通順) + \lambda_2 R(是否辭不達意) + \dots + \lambda_n R(是否總說重複的廢話)

稍微感受一下RL ChatBot的效果:

4.2SeqGAN 和 Conditional SeqGAN
前面說了這麼多,終於迎來到了高潮部分:RL + GAN for Text Generation,SeqGAN[17]站在前人RL Text Generation的肩膀上,可以說是GAN for Text Generation中的代表作。上面雖然花了大量篇幅講述RL ChatBot的種種機理,其實都是為了它來做鋪墊。試想我們使用GAN中的判別器D作為強化學習中獎勵 Reward 的來源,假設需要生成長度為T的文字序列,則對於生成文字的獎勵值 \tilde{R_{\theta}} 計算可以轉化為如下形式:
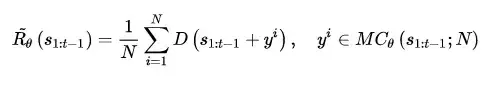
這裡要說明幾點,假設需要生成的序列總長度為 T , s_{1:t-1} 是指先前已經生成的部分序列(在RL中可視為當前的狀態),通過蒙特卡洛搜尋得到 N 種後續的序列,儘管文字生成依舊是逐詞尋找期望獎勵最大的Action(下一個詞),判別器D還是以整句為單位對生成的序列給出得分 Reward 。
在新一代的判別器 D_{next} 訓練之前,生成器 G 根據當前判別器 D 返回的得分不斷優化自己:
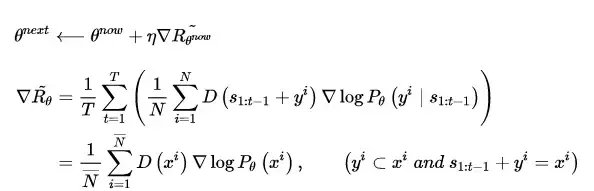
直到生成器G生成的文字足以亂真的時候,就是更新訓練新判別器的時候了。一般來說,判別器D對生成序列打出的得分既是其判斷該序列為真實樣本的概率值,按照原版GAN的理論,判別器D對於 real/fake 樣本給出的鑑定結果均為 0.5 時,說明生成器G所生成的樣本足以亂真,那麼倘若在上面的任務中,判別器屢屢對生成樣本打出接近甚至高出 0.5 的得分時,即說明判別器D需要再訓練了。在實做中為了方便,一般等待多輪生成器的訓練後,進行一次判別器的訓練。
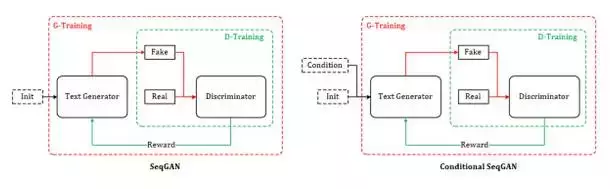
SeqGAN的提出為GAN用於對話生成(Chatbot)完成了重要的鋪墊,同樣起到鋪墊作用的還有另外一個GAN在影像生成領域的神奇應用——Conditional GAN[18~19],有條件的GAN,顧名思義就是根據一定的條件生成一定的東西,該工作根據輸入的文字描述作為條件,生成對應的影像,比如:

對話生成可以理解為同樣的模式,上一句對話作為條件,下一句應答則為要生成的資料,唯一的不同是需要生成離散的文字資料,而這個問題,SeqGAN已經幫忙解決了。綜上,我自己給它起名:Conditional SeqGAN[20]。根據4.1節以及本節的推導,Conditional SeqGAN中的優化梯度可寫成:
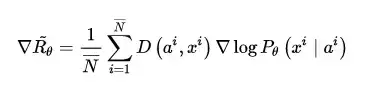
不難看出,此式子與4.1節中的變化梯度僅一字之差,只是把“打分器”給出的獎勵得分 R(a^i, x^i) 換成了鑑別器認為生成對話來自真人的概率得分 D\left(a^i, x^i \right) 。看似差別很很小,實際上 RL + GAN 的文字生成技術與單純基於RL的文字生成技術有著本質的區別:在原本的強化學習對話生成中,雖然採用了AI互相對話,並設定了 jugle 進行打分,但這個 jugle 是預訓練好的,在對話模型的訓練過程當中將不再發生變化;RL + GAN 的文字生成乃至對話模型則不同,鑑別器D與生成器G的訓練更新將交替進行,此消彼長,故而給出獎勵得分的鑑別器D在這裡是動態的(dynamic)。
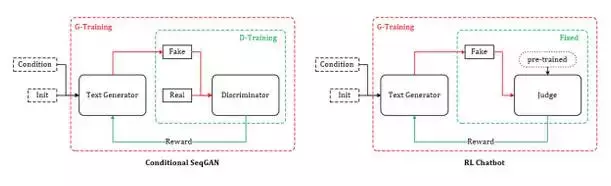
RL+ GAN 利用強化學習中的 Reward 機制以及 Policy Gradient 等技術,巧妙地避開了GAN面對離散資料時梯度無法BP的難題,在使用強化學習的方法訓練生成器G的間隙,又採用對抗學習的原版方法訓練判別器D。 在Conditional SeqGAN對話模型的一些精選結果中,RL+ GAN 訓練得到的生成器時常能返回一些類似真人的逼真回答(我真有那麼一絲絲接近“恐怖谷”的感受)。

上文所述的,只是 RL + GAN 進行文字生成的基本原理,大家知道,GAN在實際執行過程中任然存在諸多不確定因素,為了儘可能優化 GAN 文字生成的效果,而後發掘更多GAN在NLP領域的潛力,還有一些值得一提的細節。
5.1Reward Baseline:獎勵值上的 Bias
在4.2節中提到,我們採用鑑別器D給予生成樣本 x^i 的概率得分( x^i 屬於真實樣本的概率)作為獎勵 Reward ,既然是概率值,應該意識到這些概率得分都是非負的,如此一來即便生成出再差的結果,鑑別器D也不會給出負 Reward 進行懲罰。從理論上來講,生成器的訓練會趨向於降低較小獎勵值樣本 x^{low} 出現的概率而提高較大獎勵值樣本 x^{high} 出現的概率,然而在實做時,由於取樣不全等不可控因素的存在,這樣不夠分明的獎懲區別將有可能使得生成器G的訓練變得偏頗。
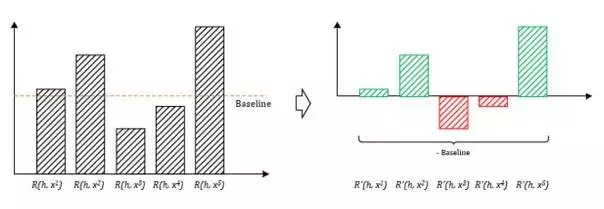
實際上,在強化學習的對話生成模型當中,就已經出現了此類問題。解決的方法很簡單,我們設定一個獎勵值 Reward 的基準值Baseline,每次計算獎勵值的時候,在後面減去這個基準值作為最終的 獎勵 or 懲罰 值,使得生成器G的生成結果每次得到的獎懲有正有負,顯得更加分明。記獎懲基準值為 b ,則4.1節中優化梯度的計算公式修改為:
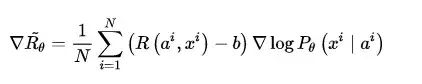
對應地,在 RL + GAN 的文字生成任務中,同樣在鑑別器D對各個生成樣本打出的概率得分上減去獎懲基準值 b ,則4.2節中 SeqGAN 與 Conditional SeqGAN 期望獎勵值的優化梯度計算公式也分別修改為如下:
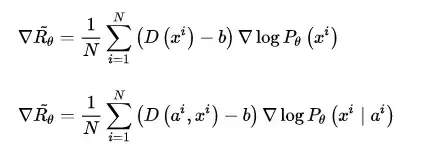
5.2REGS:一人犯錯一人當
細心的讀者可以發現,在SeqGAN的獎勵優化梯度計算公式的推導中,由鑑別器D給予的生成樣本獎勵得分其實是順應序列文字的生成過程,逐詞產生的,可以看到之前的推導公式中顯示了對於Partly文字序列的階段性獎勵值求和再求平均。然而在起初的實驗中,根據最終推導的獎勵值優化梯度計算公式,鑑別器D被訓練為用於對整句生成結果進行評估打分,這樣的話,鑑別器D的打分對於生成序列中的每一個token都是同等的存在,要獎勵就一起獎勵(獎勵值可視為相同),要懲罰就一起懲罰,這種做法會導致一個後果,看下面的例子。
比如有這樣一個對話組(包含真實回答和生成回答):

很顯然,鑑別器D能夠輕易辨識後者回答是假的,必然會給出極低的獎勵值得分,但是仔細對比真/假兩個回答可以發現,第一個詞 “我 ” 其實和真實樣本的第一個詞是一樣的,而最後一個字元 “。”其實也並無大礙,它們其實並沒有錯,真正錯誤的是 “不 ” 和 “知道 ” 這兩個詞,但很不幸,鑑別器判定 fake_answer 的整體回答是假的,原本無辜的詞項 “我 ” 和 “。” 也要跟著一起接受低分判定的懲罰。
讓我們回到 GAN + RL 對文字生成模型的優化原理,假設 P_{\theta}\left(x^i \mid a^i \right) 是面對輸入上文 a^i 時生成對話下文 x^i 的概率,我們將它拆分成逐個單詞拼接的形式,每一個出現的詞彙都將收到之前context的影響。
P_{\theta}\left(x^i \mid a^i \right) = P_{\theta}\left( x^i[1] \bracevert a^i \right) + P_{\theta}\left( x^i[2] \bracevert a^i, x^i[1] \right) + \dots + P_{\theta}\left( x^i[T] \bracevert a^i, x^i[1:T-1] \right)
在4.1,4.2節中提到,如果生成樣本 x^i 被鑑別器D打出低分(受到懲罰),生成器G將被訓練於降低產出此結果的概率。結合上面這條公式,倘若單獨將生成序列中的一部分字首 x^i[1:t] 拿出來與真實樣本中完全相同,豈不是也要接受整體低分而帶來的懲罰?
解決這一缺陷的直接方法就是把獎懲的判定粒度進一步細化到 word 或 character 級別,在文字逐詞生成的過程中對partly的生成結果進行打分。這種處理其實在SeqGAN的論文中[17]就已經實施了,擴充到Conditional SeqGAN中,優化梯度的計算公式應改寫為如下:
\nabla\tilde{R_{\theta}} = \frac{1}{N} \sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T} \left(D_e\left(a^i, x^i[1:t] \right) - b\right) \nabla\log P_{\theta}\left(x^i[t] \mid a^i, x^i[1:t-1] \right)
公式中, D_e\left(a^i, x^i[1:t] \right) 是計算的關鍵,它代表鑑別器D在文字逐詞生成過程中獲得部分文字的情況下對於最終reward的估計,簡而言之就是每得到一個新的生成詞,就結合此前生成的前序文字估計最終reward,並作為該生成詞單獨的reward,SeqGAN的論文中使用蒙特卡洛搜尋[21](Monte Carlo Search,MC search)的方法計算部分生成序列對於整體reward的估計值。而在Conditional SeqGAN的論文中,賦予了這種處理一個名字 —— Reward for Every Generation Step(REGS)。
5.3MC Search & Discriminator for Partially Decoded Sequences:準度與速度的抉擇
上一節說到SeqGAN中使用MC search進行部分序列獎勵估計值 D_e\left(a^i, x^i[1:t] \right) 的計算,作為REGS操作的關鍵計算,其難處在於,我們並不能預知部分生成序列能給我們帶來的最終結果,就好像一場籃球比賽,可能半場結束比分領先,卻也不能妄言最終的比賽結果一樣。
既然如此,在只得到部分序列的情況下, D_e\left(a^i, x^i[1:t] \right) 只得估計獲得,Monte Carlo Search[21]就是其中一種估計方法,Monte Carlo Search的思想極其簡單,假設我們已經擁有了部分生成的字首 x^i[1:t] ,我們使用當前的Generator,強制固定這個字首,並重復生成出$M$個完整的序列(有點取樣實驗的意思),分別交給鑑別器D進行打分,這 M 個模擬樣本的平均獎勵得分即為部分序列 x^i[1:t] 的獎勵估計值 D_e\left(a^i, x^i[1:t] \right) 。
D_e\left(a^i, x^i[1:t] \right) = \frac{1}{M} \sum\limits_{p=1}^{M}\left(D\left(a^i, x^i[1:t] + x_r^p[t+1:T] \right) \right)
當然,使用MC search的缺點也很明顯:每生成一個詞,就要進行 M 次生成取樣,非常耗時;還有一小點,每當我們計算較為後期的一些部分序列獎勵估計值的時候,總是會無法避免地再一次計算前面早期生成的項,這樣計算出來的 D_e\left(a^i, x^i[1:t] \right) 可能導致對於較前子序列(比如第一個詞)的過擬合。
另外一種方法提出於Conditional SeqGAN的論文,乾脆訓練一個可以對部分已生成字首進行打分的new鑑別器D。將某真實樣本的 X^+ 的全部字首子序列(必須從第一個詞開始)集合記作 \left\{x^+[1:t] \right\}_{t=1}^{T_{X^+}} ,同樣將某生成樣本$X^-$的全部字首子序列集合記作 \left\{x^-[1:t] \right\}_{t=1}^{T_{X^-}} ,我們每次從這兩者中隨機挑選一個或若干個標定為 + 或 - (與原序列相同),與原序列一同加入鑑別器D的訓練中,這樣訓練得到的Discriminator便增添了給字首子序列打分的能力,直接使用這樣的Discriminator給字首子序列打分即可獲得 D_e\left(a^i, x^i[1:t] \right) 。這種方法的耗時比起使用MC search要少很多,但得損失一定的準度。
一句話總結兩種 D_e\left(a^i, x^i[1:t] \right) 的計算方法:一種是利用部分序列YY出完整序列來給鑑別器打分,而另一種則直接將部分序列加入鑑別器的訓練過程,得到可以為部分序列打分的鑑別器,一個較慢,另一個快卻損失準度,如何選擇就看大家了。
5.4Teacher Forcing:給Generator一個榜樣
在開始講解SeqGAN中的Teacher Forcing之前,先幫助大家簡單了結一下RNN執行的兩種mode:(1). Free-running mode;(2). Teacher-Forcing mode[22]。前者就是正常的RNN執行方式:上一個state的輸出就做為下一個state的輸入,這樣做時有風險的,因為在RNN訓練的早期,靠前的state中如果出現了極差的結果,那麼後面的全部state都會受牽連,以至於最終結果非常不好也很難溯源到發生錯誤的源頭,而後者Teacher-Forcing mode的做法就是,每次不使用上一個state的輸出作為下一個state的輸入,而是直接使用ground truth的對應上一項作為下一個state的輸入。
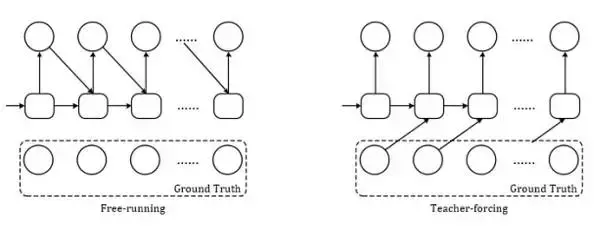
就拿Seq2Seq模型來舉例,我們假設正輸出到第三項,準備生成第四項:

Free-running mode下的decoder會將第三項錯誤的輸出 output[2] = 's'(下標從0開始)作為下一個state的輸入,而在Teacher-forcing mode下,decoder則會將正確樣本的第三項 label[2] = 'q' 作為下一個state的輸入。 當然這麼做也有它的缺點,因為依賴標籤資料,在training的時候會有較好的效果,但是在testing的時候就不能得到ground truth的支援了。最好的結果是將Free-running mode的behavior訓練得儘可能接近於Teacher-forcing mode,Professor Forcing[23]使用GAN嘗試實現了這一目標。
當然,這些都是題外話,我們要回到Teacher-Forcing mode最初的motivation:訓練(迭代)早期的RNN非常弱,幾乎不能給出好的生成結果(以至於破灌破摔,產生垃圾的output影響後面的state),必須依靠ground truth強行扶著走,才能慢慢進入正軌。
SeqGAN也存在這樣的問題,一開始的生成器G非常弱,即便是經過一定量的預訓練,也幾乎生成不出好的Result,然後這些bad result給到鑑別器D必然只能返回很低的 Reward (懲罰),生成器G的訓練只能根據鑑別器的打分來優化而無法得到good example的指導,永遠不知道什麼是好的結果,結果必然是惡性迴圈。於是,有必要在SeqGAN訓練中給到生成器G真實樣本的指導,也就是告訴生成器:“什麼樣的樣本才配得到高分 Reward ?”
4.2節中提到,生成器G 和 判別器D的訓練時交替進行的,由於鑑別器返回的打分是判定輸入樣本為真的概率,我們可以隨機取出一部分真實的樣本對話組 \mathrm{Real} = \left\{ \left(a_r^0, x_r^0 \right), \left(a_r^1, x_r^1 \right), \cdots, \left(a_r^n, x_r^n \right) \right\} ,然後直接設定他們的鑑別器獎勵值為 1 (或者其他任意定義的最高分),將它們加入生成器G的訓練過程中,這樣生成器就能知道何種樣本能得到最高的獎勵,從而一定程度上避免了SeqGAN的訓練過程由於一方的弱勢而發生崩塌。
D\left(a_r^i, x_r^i\right) = 1, \qquad \left(\left(a_r^i, x_r^i\right) \in \mathrm{Real} \right)
或者也可以這樣:用訓練好的鑑別器D也為隨機抽樣的真實樣本打分,然後加入到生成器G的訓練過程中,不過,一定要確保鑑別器D已經得到充分訓練,至少給予任意真實樣本 \left(a_r^i, x_r^i \right) 的打分要高於baseline才行(獎勵值經過偏置處理後也必須為正)。
D\left(a_r^i, x_r^i\right) > b, \qquad \left(\left(a_r^i, x_r^i\right) \in \mathrm{Real} \right)
5.5Actor-Critic:更廣義上的GAN?
在DeepMind的一篇半綜述式的文章[24]中,談到了強化學習中的另一個特殊的模型——Actor-Critic,並分析了這個模型與GAN之間的聯絡。
首先我們回顧一下GAN中鑑別器D和生成器G優化時的目標函式:
D^* = \arg\min_D -\mathbb{E}_{x \sim p_{data}}[\log D(x)] - \mathbb{E}_{z \sim \mathcal{N}\left(0, I\right)}[\log (1-D(G(z)))]
G^* = \arg\min_G \mathbb{E}_{z \sim \mathcal{N}\left(0, I\right)}[\log (1-D(G(z)))] = \arg\min_G -\mathbb{E}_{z \sim \mathcal{N}\left(0, I\right)}[\log (D(G(z)))]
再說說強化學習,在基於策略迭代的強化學習中,通過嘗試當前策略的action,從環境獲得 Reward ,然後更新策略。這種操作在遊戲實驗環境中非常有效,因為遊戲系統有封閉且清晰的環境,能夠穩定地根據各種接收到的action客觀地給出對應 Reward ,而在現實生活中,很多時候並沒有封閉清晰的環境,給定action應該得到什麼樣的 Reward 本身也不準確,只能通過設定DIY的打分器來實現,顯然這麼做很難完美model真實世界千變萬化的情況。
那麼,能不能先學習出一個能夠準確評估出獎勵值的值函式 Q^{\pi}(s,a) ,儘可能地描述環境,對各種action返回較為公正的預期獎勵呢?也就是說 Reward 的估計模型本身也是被學習的,這就是Actor-Critic,Actor部分採用傳統的Policy Gradient優化策略 \pi ,Critic部分藉助“Q-Learning”學習出最優的action-value值函式,聽起來有沒有點像GAN的模式?來看看它的目標函式,其中 \mathcal{D}\left(\cdot \Arrowvert \cdot\right) 指任意一中Divergence,值域非負當且僅當兩個分佈相同時取值為零即可(比如,KL-divergence, JS-divergence 等等):
Q^{\pi} = \arg\min_Q \mathbb{E}_{s_t, a_t \sim \pi}\left[\mathcal{D}\left(\mathbb{E}_{s_{t+1}, r_t, a_{t+1}} \left[r_t + \gamma Q\left(s_{t+1}, a_{t+1} \right) \right] \Arrowvert Q(s_t, a_t) \right) \right]
{\pi}^{\ast} = \arg\max_{\pi} \mathbb{E}_{s_0 \sim p_0, a_0 \sim \pi}\left[Q^{\pi}\left(s_0, a_0 \right) \right] = \arg\min_{\pi} -\mathbb{E}_{s_0 \sim p_0, a_0 \sim \pi}\left[Q^{\pi}\left(s_0, a_0 \right) \right]
文中將GANs模型比作一種特殊形式的Actor-Critic,並比較了兩者各自的特點以及後續的改進技術在兩者上的適配情況。試想一下,既然強化學習技術幫助GAN解決了在離散型資料上的梯度傳播問題,那麼同為強化學習的Actor-Critic也為對抗式文字生成提供了另外一種可能。

5.6IRGAN:兩個檢索模型的對抗
IRGAN[25]這篇工作發表於2017年的SIGIR,從作者的陣容來看就註定不是一篇平凡的作品,其中就包含SeqGAN的原班人馬,作者將生成對抗網路的思想應用於資訊檢索領域,卻又不拘泥於傳統GAN的經典Framework,而是利用了IR領域原本就存在的兩種不同路數的model:生成式IR模型 和 判別式IR模型。
生成式IR模型目標是產生一個query \rightarrow document的關聯度分佈,利用這個分佈對每個輸入的query返回相關的檢索結果;而判別式IR模型看上去更像是一個二類分類器,它的目標是儘可能地區分有關聯查詢對<query_r, document_r>和無關聯查詢對<query_f, document_f>,對於給定的查詢對<query, document>,判別式IR模型給出該查詢對中的兩項的關聯程度。
光從兩個模型簡單的介紹來看就能絲絲感覺到它們之間特殊的聯絡,兩種風格迥異的IR模型在GAN的思想中“有緣地”走到了對立面,我們將生成式IR模型記作: p_\theta \left(d \mid q,r \right) ,將判別式IR模型記作: f_\phi \left(q,d \right) ,於是整個IRGAN的目標函式為:
J^{G^\ast, D^\ast} = \min_{\theta} \max_{\phi} \sum\limits_{n=1}^N \left(\mathbb{E}_{d \sim p_{real}\left(d \mid q_n,r \right)}\left[\log D\left(d \mid q_n \right) \right] + \mathbb{E}_{d \sim p_{\theta}\left(d \mid q_n,r \right)}\left[\log \left(1 - D\left(d \mid q_n \right) \right)\right] \right)
在IRGAN中,鑑別器D定義為判別式IR模型的邏輯迴歸:
D\left(d \mid q \right) = \sigma \left(f_\phi \left(d,q \right) \right) = \frac{\exp \left(f_\phi \left(d,q \right) \right)}{1 + \exp \left(f_\phi \left(d,q \right) \right)}
於是鑑別器D的目標函式進一步寫為:
\phi^\ast = \arg\max_{\phi} \sum\limits_{n=1}^N \left(\mathbb{E}_{d \sim p_{real}\left(d \mid q_n,r \right)}\left[\log \left(\sigma\left(f_\phi\left(d, q_n \right)\right)\right) \right] + \mathbb{E}_{d \sim p_{\theta}\left(d \mid q_n,r \right)}\left[\log \left(1 - \sigma\left(f_\phi\left(d, q_n \right)\right) \right)\right] \right)
相對地,生成器G就直接輸出以query為condition答案池中所有document與該query的關聯分佈,不幸地,我們必須將通過這個關聯分佈,過濾出當前認為最相關的document答案,才能作為鑑別器D的輸入來判定此時此刻檢索結果的質量,原本連續型的分佈經過這一步的折騰又變成離散型的資料了,還好,我們有強化學習,設 Reward \left(\cdot \right)= \log\left(1 + \exp\left(f_\phi \left(\cdot \right) \right) \right) ,則生成器G的目標函式被寫成:
\theta^\ast = \arg\min_{\theta} \sum\limits_{n=1}^{N} \mathbb{E}_{d \sim p_{\theta}\left(d \mid q_n, r \right)}\left[\log\left(1 + \exp\left(f_\phi \left(d, q_n \right) \right) \right) \right]
也就是最大化鑑別器D給出的獎勵,而這個獎勵值主要來源於檢索結果形成的查詢對 \left(d, q_n \right) 在判別式IR模型中被認為確實有關聯的概率之和。將求和符號內的項記作: J^G \left(q_n \right) ,按照Policy Gradient的方式進行梯度優化,並使用4.1節中的推導方法描述 J^G \left(q_n \right) 的優化梯度,在實做時為了方便,取樣 k 個當前生成式IR模型給出的查詢結果求近似。
\begin{aligned} \nabla_\theta J^G \left(q_n \right) &= \nabla_\theta \mathbb{E}_{d \sim p_\theta \left(d \mid q_n, r \right)} \left[\log\left(1 + \exp\left(f_\phi \left(d, q_n \right) \right) \right) - b \right] \\ &= \sum\limits_{i=1}^{M} \nabla_\theta p_\theta \left(d_i \mid q_n, r \right) \left[\log\left(1 + \exp\left(f_\phi \left(d_i, q_n \right) \right) \right) - b \right] \\ &= \sum\limits_{i=1}^{M} p_\theta \left(d_i \mid q_n, r \right) \nabla_\theta \log p_\theta \left(d_i \mid q_n, r \right) \left[\log\left(1 + \exp\left(f_\phi \left(d_i, q_n \right) \right) \right) - b \right] \\ &\simeq \frac{1}{K} \sum\limits_{k=1}^{K} \nabla_\theta \log p_\theta \left(d_k \mid q_n, r \right) \left[\log\left(1 + \exp\left(f_\phi \left(d_k, q_n \right) \right) \right) - b \right] \end{aligned}
當然,也不能忘了我們的baseline—— b ,文中設定baseline為當前查詢結果的平均期望 Reward 。
b = \mathbb{E}_{d \sim p_\theta \left(d \mid q_n, r \right)} \left[\log\left(1 + \exp\left(f_\phi \left(d, q_n \right) \right) \right) \right]
上述是針對Pointwise情形的IR任務,不同於Pointwise情形著重於得到直接的檢索結果,Pairwise情形的IR把更多精力放在了ranking上,其返回結果 R_n = \left\{\langle d_i, d_j\rangle \mid d_i \succ d_j \right\} 中全是非對稱二元對,其中 d_i 比 d_j 與當前的查詢項關聯性更高。IRGAN也可以擴充套件到Pairwise的情形,原則是:“一切從減”。 鑑別器函式將改寫為:
D\left(\langle d_i, d_j\rangle \mid q \right) = \sigma \left(f_\phi \left(d_i, q \right) - f_\phi \left(d_j, q \right)\right) = \frac{\exp \left(f_\phi \left(d_i, q \right) - f_\phi \left(d_j, q \right)\right)}{1 + \exp \left(f_\phi \left(d_i, q \right) - f_\phi \left(d_j, q \right)\right)}
而假設生成器G是一個softmax函式,則Pairwise情形下的變形和簡化推導如下:
p_\theta \left(d_k \mid q, r\right) = \frac{\exp \left(g_\theta \left(d_k, q \right)\right)}{\sum_d\exp \left(g_\theta \left(d_k, q \right)\right)}
G\left(\langle d_k, d_j\rangle \mid q \right) = \frac{\exp \left(g_\theta \left(d_k, q \right) - g_\theta \left(d_j, q \right)\right)}{\sum_d\exp \left(g_\theta \left(d_k, q \right) - g_\theta \left(d_j, q \right) \right)} = \frac{\exp \left(g_\theta \left(d_k, q \right)\right)}{\sum_d\exp \left(g_\theta \left(d_k, q \right)\right)} = p_\theta \left(d_k \mid q, r\right)
IRGAN在Pairwise情形下的總目標函式如下,其中, o 表示真實的非對稱二元組,而 o\prime 則表示生成式IR模型生成的二元組:
J^{G^\ast, D^\ast} = \min_{\theta} \max_{\phi} \sum\limits_{n=1}^N \left(\mathbb{E}_{o \sim p_{real}\left(o \mid q_n,r \right)}\left[\log D\left(o \mid q_n \right) \right] + \mathbb{E}_{o\prime \sim p_{\theta}\left(o\prime \mid q_n,r \right)}\left[\log \left(1 - D\left(o\prime \mid q_n \right) \right)\right] \right)
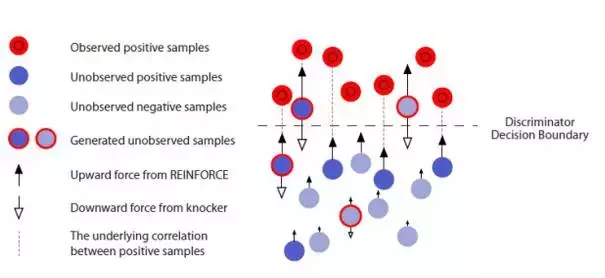
IRGAN的一大特點是,對抗model中的兩個元件各自都是一種IR模型,所以經過對抗訓練之後,不管拿出來哪個,都有希望突破原先的瓶頸。作者還關於IRGAN的訓練目標是否符合納什均衡做了一些討論,儘管在真實檢索的應用中很難獲得所謂的真實關聯分佈,但作者認為不管是觀察到的關聯樣本還是未觀察到的關聯樣本,判別IR模型的輸出總是和生成IR模型的對應輸出存在著正相關的作用力,於是也孕育而生了文中那個關於浮力和拖拽重物最終達到漂浮平衡狀態的略顯晦澀的比喻。