題目:
Given a string s, partition s such that every substring of the partition is a palindrome.
Return all possible palindrome partitioning of s.
For example, given s = "aab",
Return
[
["aa","b"],
["a","a","b"]
]
解題思路:
這道題跟Word Break II這道基本一樣,需要用DP+DFS解決
這裡採用DP中的自底向上實現,dp[i]表示前i個字元是否為切分為多個迴文字串。當求解dp[i]時,可利用已經求解的dp[i-1],
dp[i-2]…dp[1],dp[0]進行求解。
對於dp[n]的求解,我們可以將n個字元進行切分求解,分為前i個字元和後n-i個字元,i可以為(0,1,2,3,4…n-1)
假設i為1時,可根據dp[i]和後面的n-1個字元組成的單詞是否在dict中來判斷dp[n],只要i(0,1,2,3,4…n-1)其中一種
情況為真,則dp[n]為true,表示可以進行切分為多個迴文字串。
因為本題需要重構結果,所以必須要有一個資料結構來儲存每段長度的切割方案,這裡我用unordered_map<int, vector<int> >進行儲存,key為字元長度,vector儲存該key對應的切割方案。
如何求得unordered_map<int, vector<int> >中的值呢?那就應該利用求解dp[i]時,每當有一種切割方案使得dp[i]為true時,將其對應的切割位置存放到i對應的vector中,待之後用於結果重構。
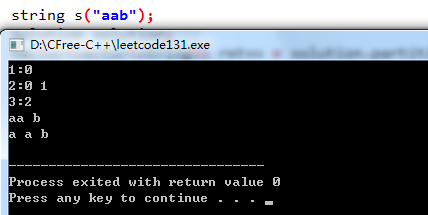
unordered_map<int, vector<int> >求得後,接下來是採用DFS演算法進行結果重構,如程式碼執行結果圖,當長度為3時,有一種切割方案,即在長度為2的位置進行切割,然後長度為2的切割方案又有兩種0和1,長度為1時,切割方案都為0,所以採用DFS時,遍歷順序為2,0然後獲得一種結果,之後回溯到2,1,因為1的切割方案為0,所以為3,1,0,又是一種結果。
實現程式碼:
#include <iostream> #include <vector> #include <iterator> #include <unordered_map> #include <string> #include <algorithm> using namespace std; /* Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s. For example, given s = "aab", Return [ ["aa","b"], ["a","a","b"] ] */ class Solution { public: //DP vector<vector<string>> partition(string s) { vector<vector<string>> retvec; if(s.size() == 0) return retvec; int len = s.size(); vector<bool> dp(len+1, false);//前i個字元是否為迴文數 dp[0] = true; unordered_map<int, vector<int>> hashtable;//對前i個字元,如果其為迴文數時的切分點 for(int i = 1; i <= len; i++) { vector<int> tmpv; for(int j = 0; j < i; j++) { if(dp[j] && isPalindrome(s.substr(j, i-j)) ) { dp[i] = true; tmpv.push_back(j); } } hashtable[i] = tmpv; } for(int k = 1; k <= len; k++) { vector<int> tvec = hashtable[k]; cout<<k<<":"; copy(tvec.begin(), tvec.end(), ostream_iterator<int>(cout, " ")); cout<<endl; } vector<int> curvec; getResult(retvec, hashtable, s, len, curvec); return retvec; } bool isPalindrome(string s) { int len = s.size(); if(len == 0) return false; for(int i = 0; i <= len/2; i++) if(s[i] != s[len-i-1]) return false; return true; } //DFS void getResult(vector<vector<string>> &retvec, unordered_map<int, vector<int>> &hashtable, string &s, int len, vector<int> &curvec) { if(len == 0) { vector<string> tv; int start = curvec.back(); for(int i = curvec.size()-2; i >= 0; i--) { int c = curvec[i]; tv.push_back(s.substr(start, c-start)); start = c; } tv.push_back(s.substr(curvec[0])); retvec.push_back(tv); return ; } vector<int> tmpv = hashtable[len]; vector<int>::iterator iter; for(iter = tmpv.begin(); iter != tmpv.end(); ++iter) { curvec.push_back(*iter); getResult(retvec, hashtable, s, *iter, curvec); curvec.pop_back(); } } }; int main(void) { string s("aab"); Solution solution; vector<vector<string>> retvv = solution.partition(s); vector<vector<string>>::iterator iter; for(iter = retvv.begin(); iter != retvv.end(); ++iter) { vector<string>::iterator it; for(it = (*iter).begin(); it != (*iter).end(); ++it) cout<<*it<<" "; cout<<endl; } return 0; }
執行結果: