先貼上上一篇部落格：這些基礎知識你都瞭解嗎？——《松本行弘的程式世界》讀書筆記（上）
上一篇講到：
- 物件導向
- 設計模式
- ajax
- MVC和猴子補丁
這一篇講《松本行弘的程式世界》書中提到的編碼、正則和數字。
7. 文字編碼
7.1 理解編碼
計算機只能處理二進位制資料，從計算機被髮明出來它是這樣，到現在還是這樣。那麼我們要讓這個只能識別“010101...”二進位制的傢伙去處理文字，該怎麼辦呢？——把文字表示成二進位制。大家可以檢視unicode（下文將介紹unicode）編碼表，看看其中中文編碼那一塊，比如，16進位制的4e07表示“萬”字：
說到這裡讓我想起來，平時我們在新聞留言、QQ聊天或者發簡訊的時候，可以發一些表情——
，大家可能都知道這些表情是用一些特殊的字串規定好的。其實，這就是一個簡單的表情編碼，和計算機中文字編碼成二進位制一個道理。
7.2 ASCII碼
當初計算機是美國人發明的，最早也在美國被應用。美國人用英語，所謂的字元只有26個英文字母，大小寫都算上，也不過52個，在算上鍵盤上那些亂七八糟的標點符號，最多100來個。於是他們發明了用7位二進位制數構成的編碼表——ASCII碼。2的7次方=128。ASCII碼可表示128個字元。計算機中8位二進位制是一個位元組，還能剩下一位，用於附加錯誤碼（作者：不知錯誤碼為何意？？）
上圖中，用二進位制數“1000001”表示的是字母“A”，十進位制是65，我們們學C語言的時候，估計都能背過——'A'轉換成int是65，現在知道什麼意思了吧。。。
下圖是ASCII碼對應的值（十進位制表示）：
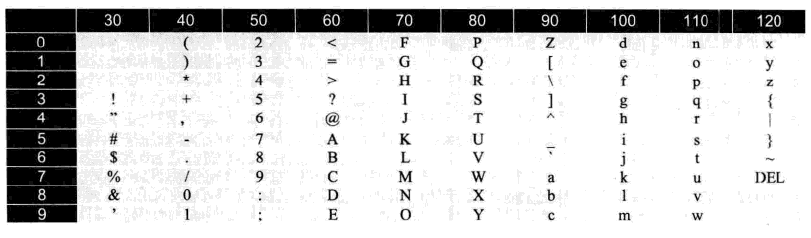
7.3 unicode字符集
世界上的文字有很多種，除了用A-Z表示的文字之外，還有許多歐洲、亞洲的文字是用其他圖形表示的，比如我們們的中文（簡體和繁體還不一樣）。於是，ASCII碼不能滿足要求之後，有出現了很多種編碼方式，例如中國的GB2312字符集。不過現在業界越來越統一到unicode字符集中。所以，就簡單介紹unicode字符集。
ASCII碼用7位二進位制，可表示128個字元，而最初的unicode字符集用16位二進位制表示，2的16次方=65536，可表示6萬多個字元。unicode字符集最初的設計者預計6W多個字元足以表示世界上所有語言文字了，可惜他們錯了。後來unicode字符集又擴充到了21位。
從網上可以查到所有unicode編碼表的內容，以下是擷取的一個片段。例如，漢字“萬”的編碼是16進位制數 4e07：
7.4 unicode的字元編碼方式
雖然unicode字符集將世界上的文字字元全部統一了編碼，但是這個編碼的儲存方式，卻又分為好幾種，例如大家常見的UTF-8、UTF-16、UTF-32。
例如，漢字“萬”的編碼值是16進位制數 4e07 ，但是通過UTF-8計算出的儲存結構和UTF-16是不一樣的。所以，如果用UTF-16的方式去解析UTF-8編碼的資料，可能會出現亂碼。
至於每種編碼方式是怎樣的，這裡就不再詳細介紹了。其實書中也只是講了一點皮毛。大家瞭解即可。
8 正規表示式
我接觸正規表示式是在學習js中接觸的，js應用正規表示式比較簡單，但是正規表示式本身的語法卻很複雜。
後來看jQuery原始碼，被sizzle這塊的正規表示式給完全搞暈了，到現在都沒梳理好。
書中介紹的無非就是正規表示式的若干語法，以及Ruby如何支援。
其實學習正規表示式不用看這個，推薦一個：正規表示式30分鐘入門教程（提醒：說30分鐘是忽悠你，用倆小時全部看完並理解，就不錯了！）
9. 整數與浮點小數
整數和浮點小數，是程式開發中最常用的型別之一。如果你覺得程式對數字的操作非常簡單，無非就是加減乘除，那麼請你耐心看完下面的文字。
9.1 整數是有範圍的
在C、C++、C#等靜態型別的語言中，int一般表示32位整數，也就是用32個二進位制數表示一個整數，除去一個符號位，int所能表現的最大整數是有限的。
C#中，int32 和 int64 分別表示不同位數的整數，都有最大值和最小值的標誌：
如果程式中的數字，超過了最大值，無法通過編譯，提示溢位。同理，如果執行時出現了這樣的情況，也會丟擲異常。
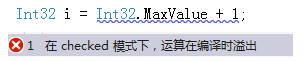
另外，不光整數有範圍。浮點小數也有範圍大小，原理一樣。
不過浮點小數還有其他要說的內容，下文介紹。
9.2 為何Ruby中的整數沒有範圍
任何語言都無法從根本上行使整數沒有範圍。Ruby是動態型別的語言，當他遇到數字超過單個整數範圍時，它會把這個數分多個整數儲存。不過這一切都是Ruby自動幫你完成的，所以在你看來，你認為Ruby的整數大小是無限制的。
這是一種技巧，類似於資料庫的分表儲存。
9.3 浮點小數的誤差
其實我從很早以前就注意到，javascript中：0.1 + 0.2 = 0.30000000000000004 ，當時只是單純的認為js對小數的計算有誤差，以後得注意。但是看完書中本章節，發現不對。不光js，所以語言都會有誤差。以C#為例：
大家可以從上圖中很清楚的看到答案。程式第一行，雖然C#輸出的是 0.1 + 0.2 = 0.3 ，但是從下面的程式可以看出，這裡的0.3只不過是個近似值。
針對浮點小數的這些計算的誤差，各個程式也都給出了他們認為的可控制的範圍。例如，C#的single型別（即float型別）中，允許誤差的可控範圍如下圖：
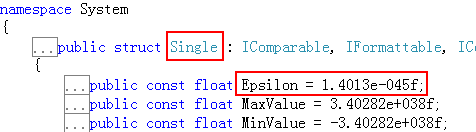
意思就是說，只要在這個範圍之內，就不認為有誤差。但是很遺憾，我還沒有用到過這個屬性。。。先了解一下吧。
9.4 計算機如何處理小數
上文說了半天的誤差，下面解釋計算機中為何對小數處理會產生誤差。原因還是一句話：計算機只能處理二進位制。
所有的整數，都可以用二進位制無誤差的表示出來，例如：65 --> 1000001，10 --> 1010 ，但是小數呢？ 有的小數無法用二進位制表示。
例如，十進位制的0.5表示為二進位制是 0.1， 但是十進位制的0.2表示為二進位制會出現一個無限迴圈的小數：0.001100110011....
這是計算機無法完全處理小數的根本！
對於計算機處理浮點數的現狀，暫時是無法改變的。它會帶來一些誤差，某些時候可能會因為一些不當的操作或者資料量的增加，而導致誤差過大，但是這也只能通過我們的演算法和設計來減輕。
最後，小數在記憶體中肯定不是以“0.25”這樣帶小數點的形式表示的，因為它必須轉換成為二進位制。書中提到了表示浮點數的IEEE745標準，也簡單介紹瞭如何將一個浮點小數表示為二進位制串，但這不是我學習的重點。因為對於這一點，先了解就好，有必要時再去深入研究。
-----------------------------------------------------------------------------------------
順便，推薦一下我錄製的《asp.net petshop4.0原始碼解讀》教程，免費學習！
-----------------------------------------------------------------------------------------
總結一下：
前文提到的文字編碼和數字，讓我想起了上一篇講過的一個詞——資料抽象化。
計算機本來只能識別二進位制碼，通過這些年來的演變，使得它可以很友好的處理我們的語言和數學知識，這怎能不叫資料抽象呢。
再說個詳細的例子，我們現在能通過印表機幾秒鐘列印一頁文字，並輕鬆閱讀，但是一開始要閱讀計算機的語言，是列印紙帶，再翻譯紙帶。大家可以試著通過ASCII碼翻譯一下這幾個字母：
