Windows phone應用開發[19]-RSA資料加密

在這個系列的第十六章節中Windows phone應用開發[16]-資料加密 中曾詳細講解過windows phone 常用的MD5,HMAC_MD5,DES,TripleDES[3DES] 資料加密的解決方案.本篇作為windows phone 資料加密一個彌補篇幅.將專門來講解windows phone rsa資料加密存在問題解決方案以及和其他平臺[Java]互通存在的問題.

RSA演算法起源與現狀

如果你關注過近現代密碼學的發展.你一定不會否認RSA的出現的重要意義.

[上圖：德國的洛倫茲密碼機，所使用的二次世界大戰加密機密郵件]

RSA 作為電腦保安通訊的基石.保證資料在傳輸過程不被第三方破解.在RSA[非對稱加密演算法]出現之前 也就是1976年之前.在通常使用資料通訊傳輸過程大多會使用[對稱演算法].簡單用如下一個使用場景來說明這個原理:

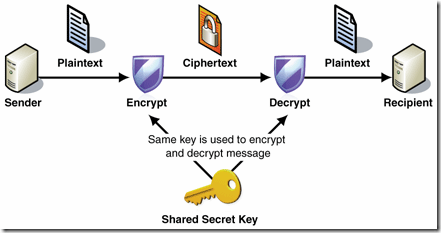
對稱演算法加密最大特點是：如果我們要從A點要向B點傳輸加密資料. 首先我們在A點採用加密演算法進行加密.加密資料傳輸給B點後. B點必須採用同樣規則才能解密.而A作為傳輸方必須告訴接收方加密規則.否則B點則無法解密. 而這個過程難以避免要傳輸和儲存密文資料的金鑰. 而一旦涉及到金鑰傳遞就存在被第三方破解和攔截的風險.

至此之後.在1977年由羅納德·李維斯特（Ron Rivest）、阿迪·薩莫爾（Adi Shamir）和倫納德·阿德曼（Leonard Adleman）三人共同提出新的加密演算法也就是現在的[非對稱加密演算法]. 這個金鑰傳輸問題才得以避免. 而RSA加密算也正是採用三人首字母命名而成的. 而其實RSA最早是在1976年，已經由Diffie和Hellman 在“New Directions in Cryptography [密碼學新方向]”一文中就已經提出. 二人在文章中提出在不傳遞金鑰的就可以實現資料的解密新構思. 而這也正是“非對稱加密演算法”最早的雛形. 正是因為二人新的構思才促使RSA基於該理論上出現.

RSA原理圖如下:

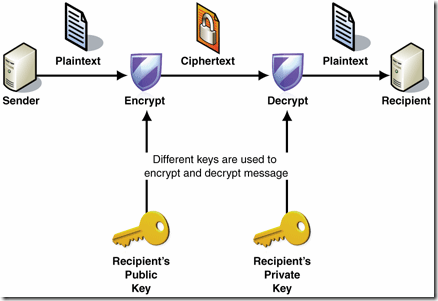
在B點可以生成兩種金鑰分別公鑰和私鑰. 公鑰是公開.任何人都可以獲得.但私鑰卻是保密的. 這樣一來資料傳輸流程就發生了變化。A點只需要獲取B點頒發的公鑰.然後對傳輸的資料進行加密. B點獲取加密資料後在採用私鑰進行解密.這樣一來採用公鑰加密資料只有採用私鑰才能解密成功.那麼只需確保私鑰的安全不被洩露.同時即使知道了演算法和若干密文不足以確定金鑰的情況.整個通訊過程都是安全的.

RSA的明文、密文是0到n-1之間的整數，通常n的大小為1024位或309位十進位制數.也就是說金鑰越長.它整個加密過程就越難以被破解.而目前被破解的最長RSA金鑰是768個二進位制位. 而基於1024位的RSA金鑰也是相對安全的[至少目前公開的資料顯示 沒有被破解的先例].RSA 金鑰是通過如下過程產生的：

A:隨機選擇兩個大素數 p, q

B:計算 N=p.q [注意 ø(N)=(p-1)(q-1)]

C:選擇 e使得1<e<ø(N),且gcd(e,ø(N))=1

D:解下列方程求出 d  [e.d=1 mod ø(N) 且 0≤d≤N]

E:公佈公鑰: KU={e,N}

F:儲存私鑰: KR={d,p,q}

其實只需要知道一些數論知識基本可以理解. 當我們知道RSA 原理後. 理論上可以通過如下三種方式來破解攻擊RSA演算法體系:

三種攻擊 RSA的方法:

A:強力窮舉金鑰

B:數學攻擊：實質上是對兩個素數乘積的分解

C:時間攻擊：依賴解密演算法的執行時間

而相對可行是採用數學方式，主要是基於因數分解的問題:

三種數學攻擊方法

A:分解 N=p.q, 因此可計算出 ø(N)，從而確定d

B:直接確定ø(N)，然後找到d

C:直接確定d

其實說到本質. 正式因為對極大整數做因數分解的難度決定了RSA演算法的可靠性。換言之，對一極大整數做因數分解愈困難，RSA演算法愈可靠。儘管如此，只有一些RSA演算法的變種^{[來源請求]}被證明為其安全性依賴於因數分解。假如有人找到一種快速因數分解的演算法的話，那麼用RSA加密的資訊的可靠性就肯定會極度下降。但找到這樣的演算法的可能性是非常小的。今天只有短的RSA鑰匙才可能被強力方式解破。到2008年為止，世界上還沒有任何可靠的攻擊RSA演算法的方式。只要其鑰匙的長度足夠長，用RSA加密的資訊實際上是不能被解破的。但在分散式計算和量子計算機理論日趨成熟的今天，RSA加密安全性受到了一定挑戰.

wp rsa資料加密

再回到本篇正題.在.NET 平臺其實早在FrameWork 2.0 時就已經提供了RSACryptoServiceProvider 來實現基於RSA演算法加密.並一直延續到windows phone 版本中.首先來看看基於windows phone 平臺做一個最簡單加密“Hello World”. 構建一個空白的Project .實現起來非常簡單：

RSACryptoServiceProvider rsa = new System.Security.Cryptography.RSACryptoServiceProvider();
byte[] contentBytes = System.Text.Encoding.UTF8.GetBytes(“Hello World”);
return Convert.ToBase64String(rsa.Encrypt(contentBytes, false));

首先宣告一個RSACryptoServiceProvider 物件,然後對需要加密的資料採用UTF8格式編碼成位元組陣列.在採用RSACryptoServiceProvider物件的Encrypt()方法執行加密.加密資料因為返回時位元組陣列轉換成Base64字串可見.

做到這肯定有人會問RSA加密結果成不是採用公鑰和私鑰嗎? 那RSACryptoServiceProvider物件公鑰和私鑰在那?我們也可以採用如下程式碼來檢視:

RSACryptoServiceProvider rsa= new System.Security.Cryptography.RSACryptoServiceProvider();
rsa.ExportParameters(true);

ExportParameters()方法會返回一個RSAParameters結構的物件. 方法的引數True和False用來標識匯出的RSAParameters物件是否包含私有引數. 其實當我們採用預設的建構函式例項化一個RSACryptoServiceProvider物件時..net會幫我們預設生成一對公鑰和私鑰.可以通過呼叫其ExportParameters()方法或ToXmlString()[WP中沒有改方法]方法匯出金鑰.在看來看RSAParameters結構包含的引數屬性:

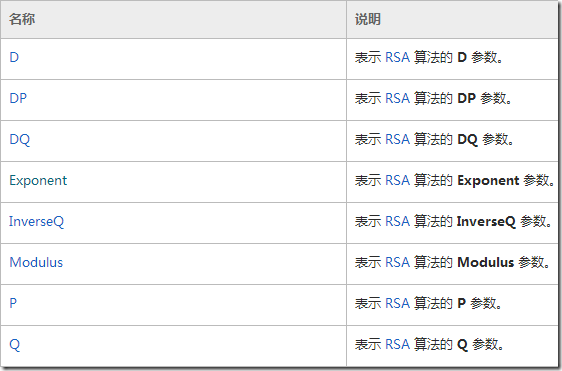
其實如上可以發現這些引數正式生成RSA公鑰和金鑰需要的引數. P和Q代表兩個大素數.D代表私鑰指數.Exponent代表公鑰指數.把匯出的預設的RSAParameters物件可以看到公鑰指數指數是65537. 這是微軟選擇預設構造方法時生成的公鑰都是一樣的.65537轉換成位元組陣列就是Exponent的值. 而AQAB正是65337 Base64編碼而來. 但當我們把這個位元組陣列轉換成Base64String看一下結果:

Console.WriteLine(Convert.ToBase64String(Encoding.Default.GetBytes("65537")));

輸出卻是”NjU1Mzc=” 而並不是我們預想的AQAB. 其實65337 是一個大素數. 我們不能把其當做一個普通的字串來直接處理. 首先我們需要把它轉換成一個二進位制位元組陣列,每8位一擷取. 依次取6位每個前面加上“00”. 轉換十進位制就是我們對應資料. 當然更多細節可以參考如下這篇文章.

其實整個加密過程就像一個臨時的回話Session.如果我們加密資料對外使用是就需要進行傳遞. 我們就需要對這個臨時回話的RSA公鑰和私鑰進行儲存.但更多的應用場景裡我們會發現實際專案中一般情況採用公鑰證照也就是[.Cer]檔案來儲存和傳遞公鑰. 然後應用程式中匯入公鑰檔案中的資料.來進行加密資料. 而把一個檔案的位元組流陣列轉換我們需要公鑰物件RSAParameter物件,這時我們需要用到X509PublicKeyParser這個類. 但遺憾的是目前Windows Phone 並沒有提供這個類的實現.但在C-Sharper上已經有人完整移植了該版本.完整的類如下：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Security.Cryptography;
using System.Security.Cryptography.X509Certificates;
using System.Text;

namespace System.Security.Cryptography
{
    internal abstract class AbstractAsn1Container
    {
        #region Property
        private int offset;
        private byte[] data;
        private byte tag;
        #endregion

        #region Action
        internal protected AbstractAsn1Container(byte[] abyte, int i, byte tag)
        {
            this.tag = tag;
            if (abyte[i] != tag)
            {
                throw new Exception("Invalid data. The tag byte is not valid");
            }
            int length = DetermineLength(abyte, i + 1);
            int bytesInLengthField = DetermineLengthLen(abyte, i + 1);
            int start = i + bytesInLengthField + 1;
            this.offset = start + length;
            data = new byte[length];
            Array.Copy(abyte, start, data, 0, length);
        }

        internal int Offset
        {
            get
            {
                return offset;
            }
        }

        internal byte[] Bytes
        {
            get
            {
                return this.data;
            }
        }

        internal protected virtual int DetermineLengthLen(byte[] abyte0, int i)
        {
            int j = abyte0[i] & 0xff;
            switch (j)
            {
                case 129:
                    return 2;


                case 130:
                    return 3;


                case 131:
                    return 4;


                case 132:
                    return 5;


                case 128:
                default:
                    return 1;
            }
        }

        internal protected virtual int DetermineLength(byte[] abyte0, int i)
        {
            int j = abyte0[i] & 0xff;
            switch (j)
            {
                case 128:
                    return DetermineIndefiniteLength(abyte0, i);


                case 129:
                    return abyte0[i + 1] & 0xff;


                case 130:
                    int k = (abyte0[i + 1] & 0xff) << 8;
                    k |= abyte0[i + 2] & 0xff;
                    return k;


                case 131:
                    int l = (abyte0[i + 1] & 0xff) << 16;
                    l |= (abyte0[i + 2] & 0xff) << 8;
                    l |= abyte0[i + 3] & 0xff;
                    return l;
            }
            return j;
        }

        internal protected virtual int DetermineIndefiniteLength(byte[] abyte0, int i)
        {
            if ((abyte0[i - 1] & 0xff & 0x20) == 0)
                throw new Exception("Invalid indefinite length.");
            int j = 0;
            int k;
            int l;
            for (i++; abyte0[i] != 0 && abyte0[i + 1] != 0; i += 1 + k + l)
            {
                j++;
                k = DetermineLengthLen(abyte0, i + 1);
                j += k;
                l = DetermineLength(abyte0, i + 1);
                j += l;
            }


            return j;
        }
        #endregion
    }

    #region Internal Object
    internal class IntegerContainer : AbstractAsn1Container
    {
        internal IntegerContainer(byte[] abyte, int i)
            : base(abyte, i, 0x2)
        {
        }
    }

    internal class SequenceContainer : AbstractAsn1Container
    {
        internal SequenceContainer(byte[] abyte, int i)
            : base(abyte, i, 0x30)
        {
        }
    }

    public class X509PublicKeyParser
    {
        public static RSAParameters GetRSAPublicKeyParameters(byte[] bytes)
        {
            return GetRSAPublicKeyParameters(bytes, 0);
        }


        public static RSAParameters GetRSAPublicKeyParameters(byte[] bytes, int i)
        {
            SequenceContainer seq = new SequenceContainer(bytes, i);
            IntegerContainer modContainer = new IntegerContainer(seq.Bytes, 0);
            IntegerContainer expContainer = new IntegerContainer(seq.Bytes, modContainer.Offset);
            return LoadKeyData(modContainer.Bytes, 0, modContainer.Bytes.Length, expContainer.Bytes, 0, expContainer.Bytes.Length);
        }


        public static RSAParameters GetRSAPublicKeyParameters(X509Certificate cert)
        {
            return GetRSAPublicKeyParameters(cert.GetPublicKey(), 0);
        }


        private static RSAParameters LoadKeyData(byte[] abyte0, int i, int j, byte[] abyte1, int k, int l)
        {
            byte[] modulus = null;
            byte[] publicExponent = null;
            for (; abyte0[i] == 0; i++)
                j--;


            modulus = new byte[j];
            Array.Copy(abyte0, i, modulus, 0, j);
            int i1 = modulus.Length * 8;
            int j1 = modulus[0] & 0xff;
            for (int k1 = j1 & 0x80; k1 == 0; k1 = j1 << 1 & 0xff)
                i1--;


            if (i1 < 256 || i1 > 4096)
                throw new Exception("Invalid RSA modulus size.");
            for (; abyte1[k] == 0; k++)
                l--;


            publicExponent = new byte[l];
            Array.Copy(abyte1, k, publicExponent, 0, l);
            RSAParameters p = new RSAParameters();
            p.Modulus = modulus;
            p.Exponent = publicExponent;
            return p;
        }
    }

    #endregion
}

那麼拿到這個類的實現.我們可以在windows phone 實現把公鑰檔案[.cer]位元組流資料轉換公鑰資訊RSAParameters物件匯入到應用程式中.匯出公鑰PublicKey方法可以採用如下程式碼實現:

private System.Security.Cryptography.RSAParameters ConvertPublicKeyToRsaInfo()
{
   System.Security.Cryptography.RSAParameters RSAKeyInfo;
   using (var cerStream = Application.GetResourceStream(new Uri("/RSAEncryptDemo;component/Files/DemoPublicKey.cer", UriKind.RelativeOrAbsolute)).Stream)
   {
      byte[] cerBuffer = new byte[cerStream.Length];
      cerStream.Read(cerBuffer, 0, cerBuffer.Length);
      System.Security.Cryptography.X509Certificates.X509Certificate cer = new System.Security.Cryptography.X509Certificates.X509Certificate(cerBuffer);
      RSAKeyInfo = X509PublicKeyParser.GetRSAPublicKeyParameters(cer.GetPublicKey());
   }
   return RSAKeyInfo;
}

在執行這段程式碼你需要保證新增進來引入的公鑰.Cer檔案是作為專案資源被訪問的.Build Action 設定為Resource. 這樣我們就可以直接通過通過公鑰檔案的方式來獲取公鑰資料的資訊.然後再預設構建的RSACryptoServiceProvider物件中通過ImportParameters()方法匯入公鑰資訊：

RSACryptoServiceProvider rsa = new System.Security.Cryptography.RSACryptoServiceProvider();
rsa.FromXmlString(publickey);
RSAParameters publicKey = ConvertPublicKeyToRsaInfo();
rsa.ImportParameters(publicKey);

其實預設的RSACryptoServiceProvider物件也可以採用XMl格式來匯入公鑰資料. 但前提是你需要知道公鑰的Modulus和Exponent對應的值.但大多情況我們拿到公鑰檔案來實現跨平臺傳遞資訊的.如果需要這兩個公鑰欄位資料. 我們可以通過伺服器端通過介面來傳遞公鑰的資訊. RSA特點就是公鑰是可以公開的.只要保證私鑰是保密即可實現加密. 所以這種傳遞完全可行的. 拿到公鑰資料後然後組合成對應XML 格式匯入RSACryptoServiceProvider物件中.程式碼實現如下：

//匯入檔案方式代替 伺服器介面的資料 原理是一至的
RSAParameters rsaDefineRap = ConvertPublicKeyToRsaInfo();
string modulus = Convert.ToBase64String(rsaDefineRap.Modulus);
string exponent = Convert.ToBase64String(rsaDefineRap.Exponent);

string publickey = @"<RSAKeyValue><Modulus>" + modulus + "</Modulus><Exponent>" + exponent + "</Exponent></RSAKeyValue>";
RSACryptoServiceProvider rsa= new System.Security.Cryptography.RSACryptoServiceProvider();
rsa.FromXmlString(publickey);

當我們拿到公鑰的資料需要對拿到Byte位元組資料進行Base64String編碼.然後通過如上格式[不能錯]拼接XML字串.在通過FromXmlString()方法匯入.也可以同樣實現公鑰資訊的匯入.在做Windows phone RSA 我也看到有人在Windows 8也遇到匯入公鑰的問題[Windows 8 系列（四）：Win8 RSA加密相關問題]. 這個主要因為Windows 8匯入公鑰資料採用ASC編碼.公鑰資訊頭資料缺失導致的. 這個問題解決方案另外博文會說到.

如上我們採用兩種方式來匯入公鑰PublicKey資料.拿到公鑰資料後我們採用我麼自己公鑰進行資料加密 加密操作程式碼如下:

RSAParameters rsaDefineRap = ConvertPublicKeyToRsaInfo();
string modulus = Convert.ToBase64String(rsaDefineRap.Modulus);
string exponent = Convert.ToBase64String(rsaDefineRap.Exponent);

//Import Public Key
string publickey = @"<RSAKeyValue><Modulus>" + modulus + "</Modulus><Exponent>" + exponent + "</Exponent></RSAKeyValue>";
RSACryptoServiceProvider rsaCrypt = new System.Security.Cryptography.RSACryptoServiceProvider();
rsaCrypt.FromXmlString(publickey);

//Data Encrypt
byte[] encryBytes=  rsaCrypt.Encrypt(System.Text.Encoding.UTF8.GetBytes("Hello World"), false);
return Convert.ToBase64String(encryBytes);

發現加密資料成功.在執行加密操作Encrypt()方法中很多人會碰到CryptographicException Message 為Bad Length的異常 如下：

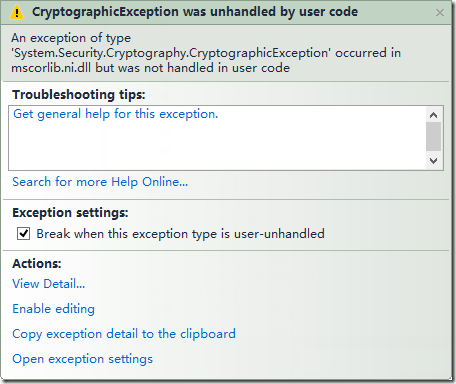
Bad Length Exception.剛開始除錯時特別頻繁.這個異常主要問題是因為加密的資料長度超過公鑰能夠加密資料的範圍導致的. 在RSA中我們能夠加密資料的大小取決於公鑰的長度大小.公鑰長度和保密之間區別如下：

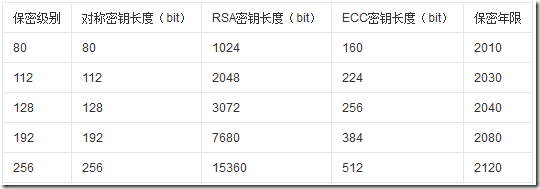
RSA的資料加密大多是針對資料量較小的. 首先需要確認當前公鑰大小是多Bit.我們目前演示的公鑰檔案.cer是1024 Bit的. Padding填充演算法是[PKCS # 1 V1.5]，ok 那麼我們為了避免在加密操作出現這個異常我們需要加密資料大小Size進行判斷. 可以採用如下方法來判斷：

        private bool IsOverEncryptStrMaxSize(int encryptDataSize)
        {
            bool isOver = false;
            if (!IsDoOAEPPadding)
            {
                #region When Encrypt Is Does't Need Padding Operator
                int MaxBlockSize = ((KeySize - 384) / 8) + 37;
                if (encryptDataSize > MaxBlockSize)
                    isOver = true;
                #endregion
            }
            else
            {
                #region When Encrypt Is Need Padd Operator
                int MaxBlockSize = ((KeySize - 384) / 8) + 7;
                if (encryptDataSize > MaxBlockSize)
                    isOver = true;
                #endregion
            }
            return isOver;
        }

引數encryptDataSize 是當前把需要加密的資料轉換成位元組陣列的長度. IsDoOAEPPanding是判斷是否採用填充演算法.這裡需要說明的是:

   byte[] encryBytes=  rsaCrypt.Encrypt(System.Text.Encoding.UTF8.GetBytes("Hello World"), false);

加密操作. 如果採用False則預設RSA加密採用填充演算法是[PKCS#1 1.5]Ps:我們證照一致. 如果為true.則對應加密填充演算法是OAEP填充方式.目前.NET在RSA只支援[OAEP & PKCS#1 1.5]兩種填充演算法.當然還有更多.後買會講到.我們這裡採用FAlse也就是[PKCS#1 1.5]和我們證照保持一致. 如果這樣我們通過該方法計算.如果是1024 Bit大小的公鑰能夠加密的資料是117個位元組. 同理可以推斷2048Bit 能夠加密 245位元組. 也就是說我們目前能夠加密的不能夠超過1024Bit對應的117個位元組. 如果超過這個位元組 就會丟擲Bad Length異常.

有人說我要採用RSA加密一個整個Xml檔案.這就涉及到另外一個問題-RSA如何加密到大資料. 可以參考StackOverFllow 給出解決方案[RSA of large file using C# [duplicate] .其實核心的原理資訊頭採用RSA進行加密.主幹內容也就是大資料內容採用的3DES配合進行加密. 解密是採用相同規則解密即可.並無難度. 如果需要解決我會在另外一個章節講到.

如果是windows phone 我並不推薦你加密整個檔案或是其他特別大的資料方式.如果你的資料小於1M 以內. 採用RSA加密. 並不推薦直接加密整個資料內容. 而是在加密前.把整個資料進行MD5加密.這樣一來幾百位元組資料內容會被生成一個唯一的16位或32為大小的字元進行代替. 然後把MD5 對應的字元資料進行加密.就不會出現大資料加密時Bad Length異常.當然解密時也需要同樣的規則. RSA加密前規則和解密必須保證一致.即可.

跨平臺互通

RSA在客戶端加密一般要涉及到伺服器端的解密. 而伺服器端大多采用其他平臺構建的.類似Java. 在除錯時大多情況會碰到客戶端加密已經成功.而伺服器端一值無法解密.存在互通的問題.

首先來看一個基本問題我們在客戶端採用如上加密方式來加密同一個MD5 字串:

//MD5 String
7E9667A96C301BF79979E49956D189C7

加密兩次檢視檢視同一個公鑰對同一條資料的加密結果:

//First
tbn5ejK21uJxObBYRp1Bh8k9FrmMWDFKRuithTKU7OITeO8Wss+j6Q3FAcE7x7EA1KpPMhCgnIj6BbQlw+Xeat8Kj/s8SLH3Vel0UPS3+gvshDW8vm2qQsPlsbg3HQ7xD6P/OLdnRleOY9VWG31n3ZouYEKJp2G0FnK/w2VD9zs=

//Second
lMw9QaU8MtXvyknEv2M9RNGcOR2UQKC44BD4i95seBjBnthcXosGh9O9DCYBEQuMNTTXX8pI5ipUwEBJNKbN4jmx7lPoxg4khxbmgaofq71sd1hFwY58Or29lxprm4dXPHkM2LsgifRazlpddHN3lKszH3i065fy8LJcrNmZmCU=

很明顯我們發現在同一公鑰針對同一條資料加密結果居然是不一致的.而同樣的演算法在Java針對同一條資料加密始終都是一致的.

這裡需要說明的是在.net平臺上為了保證RSA加密演算法的安全性.在每次加密的時候都會生成一定的隨機數和原始資料一塊被加密.導致每次加密的結果因為新增隨機數不同加密結果也不一致.其實這些隨機數也是遵循演算法標準的.也就是上面提到的隨機填充演算法.比如NoPadding、ISO10126Padding、OAEPPadding、PKCS1Padding、PKCS5Padding、SSL3Padding，而最常見的應該是OAEPPadding【Optimal Asymmetric Encryption Padding】、PKCS1Padding；.Net支援PKCS1Padding或OAEPPadding，其中OAEPPadding僅在XP或更高版本的作業系統上可用.

Java的實現，主要通過Cipher.getInstance實現，傳入的引數是描述為產生某種輸出而在給定的輸入上執行的操作（或一組操作）的字串。必須包括加密演算法的名稱，後面可能跟有一個反饋模式和填充方案。這樣的實現就比較靈活，我們可以通過引數指定不同的反饋模式和填充方案；比如Cipher.getInstance("RSA/ECB/PKCS1Padding")，或者Cipher.getInstance("RSA")均可，但用其加密的效果也會不一樣.

NET平臺加入隨機數的概念.當採用.NEt 平臺加密後.在通過Java伺服器端解密時因Java採用的是標準的RSA加密.不新增隨機數的. 導致java平臺伺服器端解密失敗.這個時候回導致.NET 加密資料無法與Java平臺的互通.

解決這個問題有兩種思路:

A：在.NET 客戶端採用剔除掉加密時新增的隨機數. 採用標準的RSA演算法加密資料. Java伺服器端採用標準RSA解密即可

B：.NET客戶端和Java伺服器端採用相同隨機數填充標準. 實現一致的資料加密和解密操作.

思路A.其實現在。NEt FrameWork提供的RSACryptoServiceProvider物件因為在家隨機數. 我們需要自己實現一個標準的RSA演算法. 然後對需要加密資料進行加密.針對windows phone 標準的RSA演算法移植程式碼可以參考[C# BigInteger Class]： 這裡移植版本.這樣一來我們加密操作就採用BitInteger類來進行 程式碼如下：

System.Security.Cryptography.RSAParameters RSAKeyInfo = ConvertPublicKeyToRsaInfo();
BigInteger bi_e = new BigInteger(RSAKeyInfo.Exponent);
BigInteger bi_n = new BigInteger(RSAKeyInfo.Modulus);

BigInteger bi_data = new BigInteger(System.Text.Encoding.UTF8.GetBytes("Hello World"));//
BigInteger bi_encrypted = bi_data.modPow(bi_e, bi_n);
return bi_encrypted.getBytes();

.NET客戶端構建一個公鑰對應的BigInteger e、一個模對應的BigInteger n和一個明文對應的BigInteger m，然後執行語句BigInteger c=m.modPow(e,n)，便可以實現加密操作，密文為c，這樣的加密是標準加密，沒有附加任何填充演算法的加密. 然對加密資料進行Base64String編碼. 在傳遞伺服器端解密驗證.通過.

思路B.如果.net和Java 平臺在進行RSA加密時採用的填充保持標準一致. 那麼Java和.net 平臺資料加密和解密.即使每次加密資料結果都一致.也是可以互通的.而.NET 平臺目前只是實現兩種填充方式.[OAEP & PKCS#1 1.5]. 而Java平臺恰好支援其中的PKCS#1 1.5. 這樣一來我們可以採用統一的填充標準加密即可.

rsa.Encrypt(contentBytes, false)

加密時設定是否填充為False.也就是採用預設的PKC#1 1.5填充標準.

但除錯依然發現伺服器端解密失敗. 經歷過很長一段時間都搞不清楚這個問題具體出在哪.直到我看到MSDN上關於RSACryptoServiceProvider物件Remark裡賣弄描述.瞬間明白這個問題出在那如下：

Remark:

This is the default implementation of RSA.

The RSACryptoServiceProvider supports key lengths from 384 bits to 16384 bits in increments of 8 bits if you have the Microsoft Enhanced Cryptographic Provider installed. It supports key lengths from 384 bits to 512 bits in increments of 8 bits if you have the Microsoft Base Cryptographic Provider installed.

Interoperation with the Microsoft Cryptographic API (CAPI)

Unlike the RSA implementation in unmanaged CAPI, the RSACryptoServiceProvider class reverses the order of an encrypted array of bytes after encryption and before decryption. By default, data encrypted by the RSACryptoServiceProvider class cannot be decrypted by the CAPI CryptDecrypt function and data encrypted by the CAPI CryptEncrypt method cannot be decrypted by the RSACryptoServiceProvider class.

If you do not compensate for the reverse ordering when interoperating between APIs, the RSACryptoServiceProvider class throws a CryptographicException.

To interoperate with CAPI, you must manually reverse the order of encrypted bytes before the encrypted data interoperates with another API. You can easily reverse the order of a managed byte array by calling the Array.Reverse method.

你看到了吧.最後兩段譯文：

預設情況下，CAPI CryptDecrypt 函式無法解密由 RSACryptoServiceProvider 類加密的資料，RSACryptoServiceProvider 類無法解密由 CAPI CryptEncrypt 方法加密的資料。

如果在 API 之間互相操作時沒有對顛倒的順序進行補償，RSACryptoServiceProvider 類會引發 CryptographicException。

要同 CAPI 相互操作，必須在加密資料與其他 API 相互操作之前，手動顛倒加密位元組的順序。 通過呼叫 Array.Reverse 方法可輕鬆顛倒託管位元組陣列的順序

也就是說。net平臺對標準的RSA演算法位元組陣列採用自動翻轉.你要是還原到標準的加密結果需要採用Array.Reverse()方法翻轉過來/.[汗啊].我採用系統物件加密採用Reverse（）操作發現Java伺服器端解密成功了 完成程式碼如下：

           #region Get Data Encrypt Public Key
            RSAParameters rsaDefineRap = ConvertPublicKeyToRsaInfo();
            string modulus = Convert.ToBase64String(rsaDefineRap.Modulus);
            string exponent = Convert.ToBase64String(rsaDefineRap.Exponent);
            string publickey = @"<RSAKeyValue><Modulus>" + modulus + "</Modulus><Exponent>" + exponent + "</Exponent></RSAKeyValue>";

            RSACryptoServiceProvider rsa = new System.Security.Cryptography.RSACryptoServiceProvider();
            rsa.ImportParameters(rsaDefineRap);
            //rsa.ExportParameters(false);

            #region Control Encrypt To Md5 Format String
            string encryptWithMd5Str = MD5Core.GetHashString(needEncryptStr);
            #endregion

            #region Encrypt Not Over The Max Size
            byte[] needEncryptBytes = System.Text.UTF8Encoding.UTF8.GetBytes(encryptWithMd5Str);
            byte[] encryptBytes = null;
            if (!IsOverEncryptStrMaxSize(needEncryptBytes.Length))
            {
                encryptBytes = rsa.Encrypt(needEncryptBytes, IsDoOAEPPadding);
                if (encryptBytes != null)
                    encryptBytes.Reverse();
            }
            #endregion

            return encryptBytes == null ? "" : Convert.ToBase64String(encryptBytes);
            #endregion

如果你在最後資料加密成功後忘了這段程式碼：

  if (encryptBytes != null)
      encryptBytes.Reverse();

我只能對你說God Bless you.

如上兩種思路分別都能實現.NET 和Java平臺的互通.其中思路B的方式最為廉價.只需要確保兩個平臺之間填充演算法一致. 然後對加密結果進行Reverse()翻轉操作即可.這個問題在我看到MSDN文件REmark文件突然就釋然了.

核心程式碼都在上面.需要原始碼在直接@我把. 等我整理上傳到Github上[https://github.com/chenkai]

Contact [@chenkaihome]

參考資料：

C# BigInteger Class

RSACryptoServiceProvider   

Why does my Java RSA encryption give me an Arithmetic Exception?

Java RSA Encrypt - Decrypt .NET - need help