對二叉樹遍歷操作的深入思考
已知某棵二叉樹,容易求得它的某種遍歷序列,但是,反過來,若已知某種遍歷序列,是否可以唯一確定一棵二叉樹呢?
1、若已知先/中/後序序列......
例:已知先序列為0-1-2-3-4-5-6-7-8
對應情況:
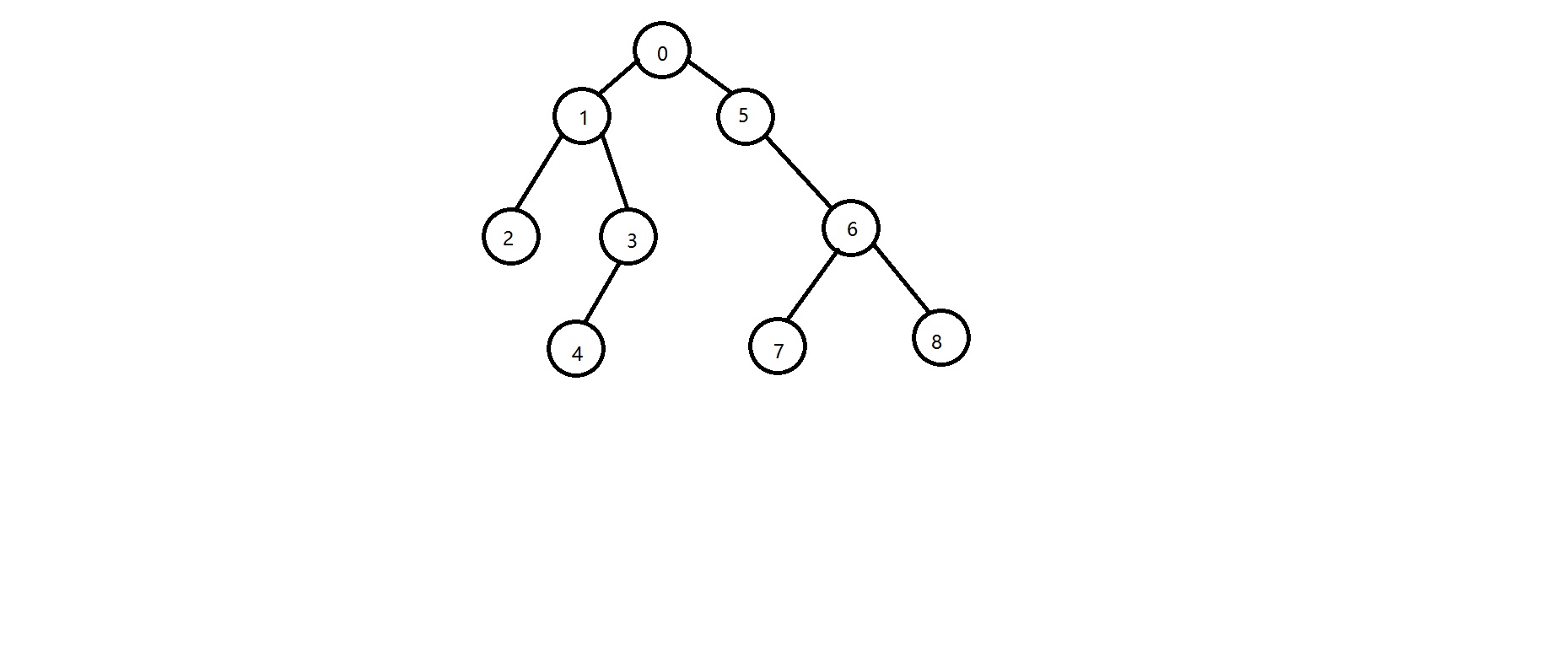
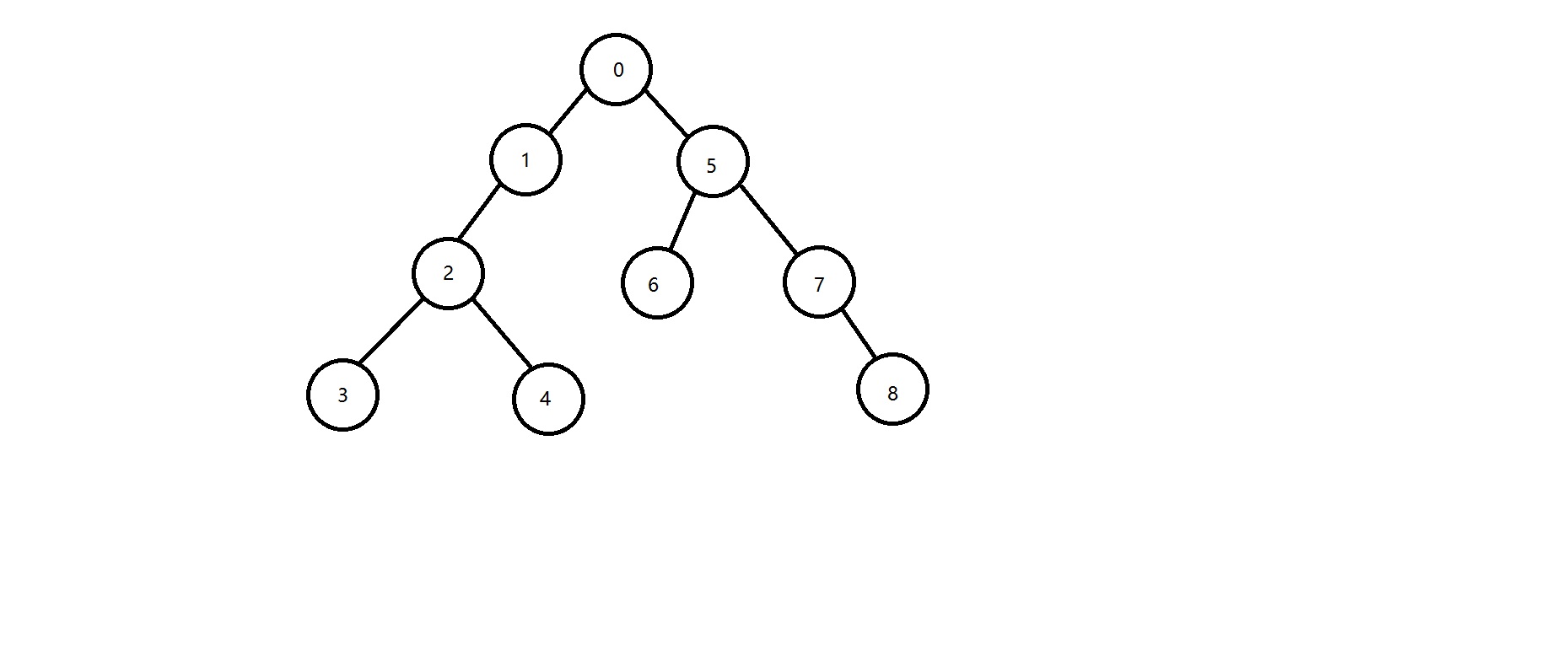
可以看到,兩幅圖片雖然先序是一樣的,但兩棵樹完全是不同的兩棵樹。
2、若已知中序和後序序列......
例:
已知中序遍歷:B D C E A F H G
已知後序遍歷:D E C B H G F A
結果:
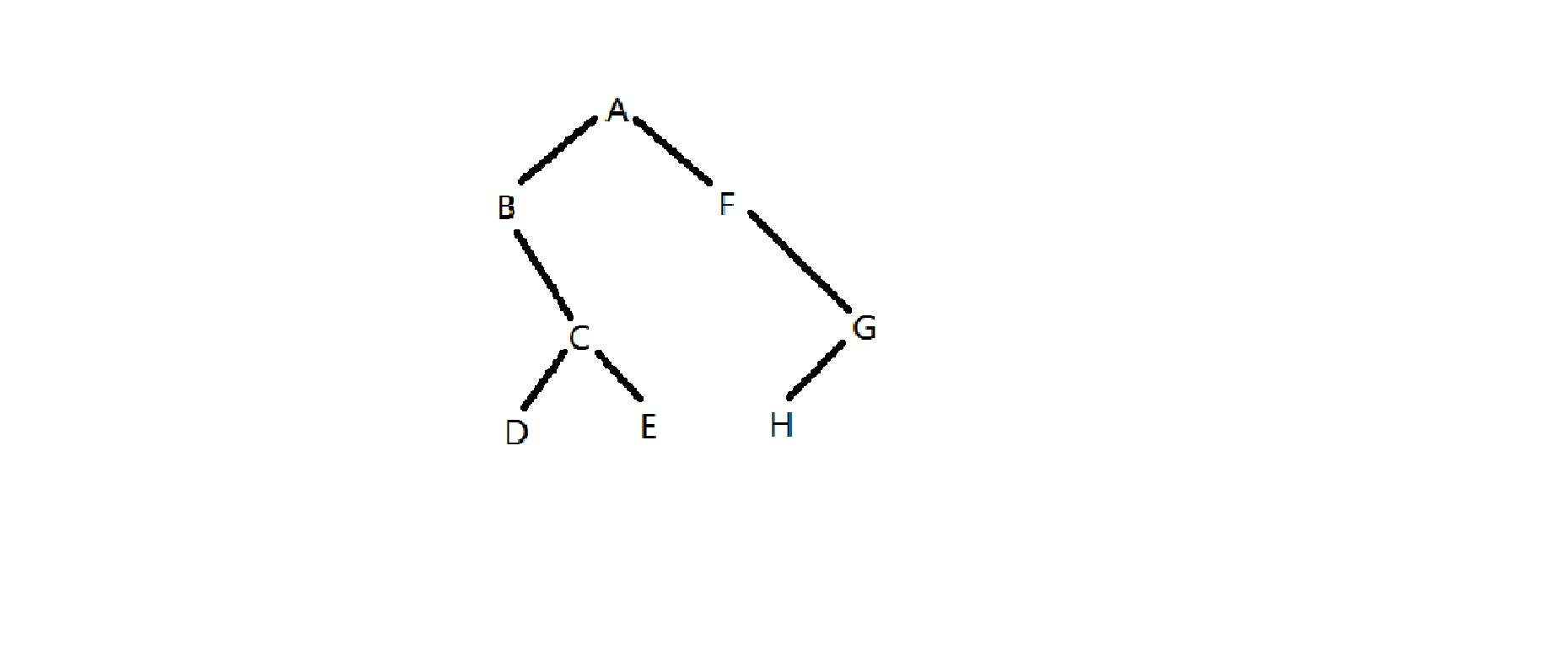
推斷過程:
- (1)從後序遍歷表中以及後序的性質,可以判定A是根

(2)從中序遍歷表中以及中序的性質,加以條件(1)以知道BDCE是A的左子數,FHG是A的右子樹

(3)先看FGH,在後序遍歷中可以看到順序是HGF可以說明F是A的右結點;看中序遍歷可以看到順序是FHG,如果F有左子結點的話,根據中序遍歷的性質,中序遍歷表中A的後面絕逼不是F,但結果是F,說明F沒有左結點;要實現在中序遍歷中,F後面的結點排布是H G的話,就要使H是G的左節點,綜上所述,這一步可以得到這麼個結果:
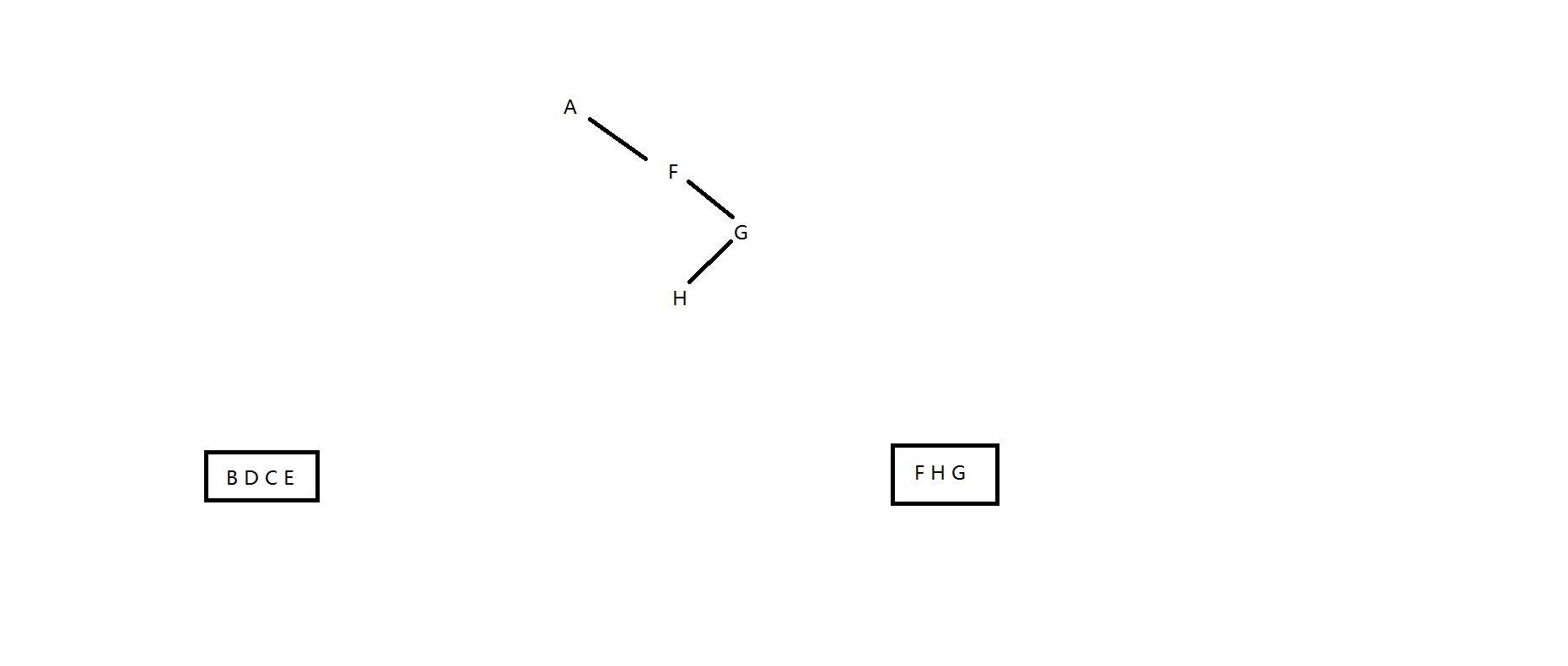
- (4)再看BDCE,從中序遍歷可以看到順序為:BDCE,若B有左子結點,則第一個不會是B,說明B並沒有左子結點;從後序遍歷中可以看到,順序為:DECB,說明B是A的左子結點;剩下DCE,根據中序遍歷,我有兩種猜想
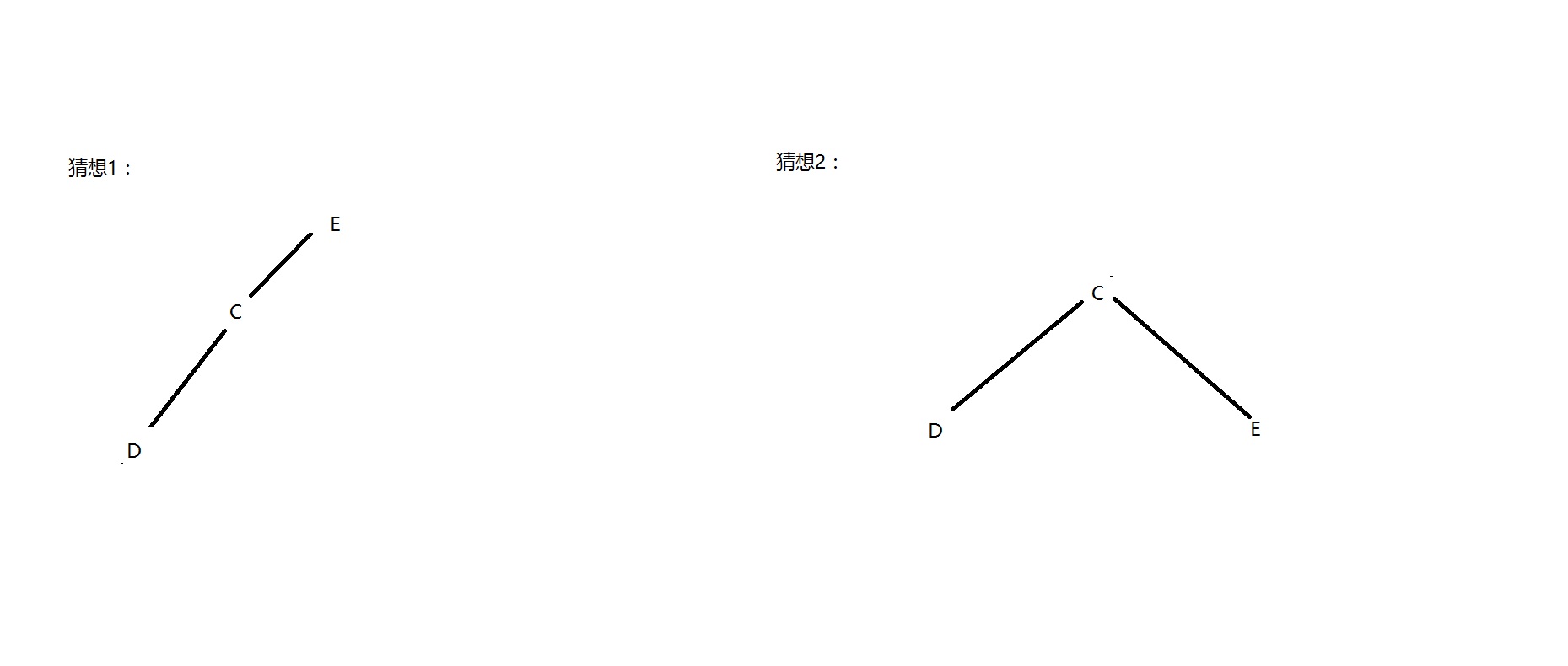
但是根據後序遍歷所示,順序為:DEC,對於第一種猜想,應該E是D的根,與猜想1的情況出入,因此猜想2為正確的,綜上所述,可以得到這麼個結果:
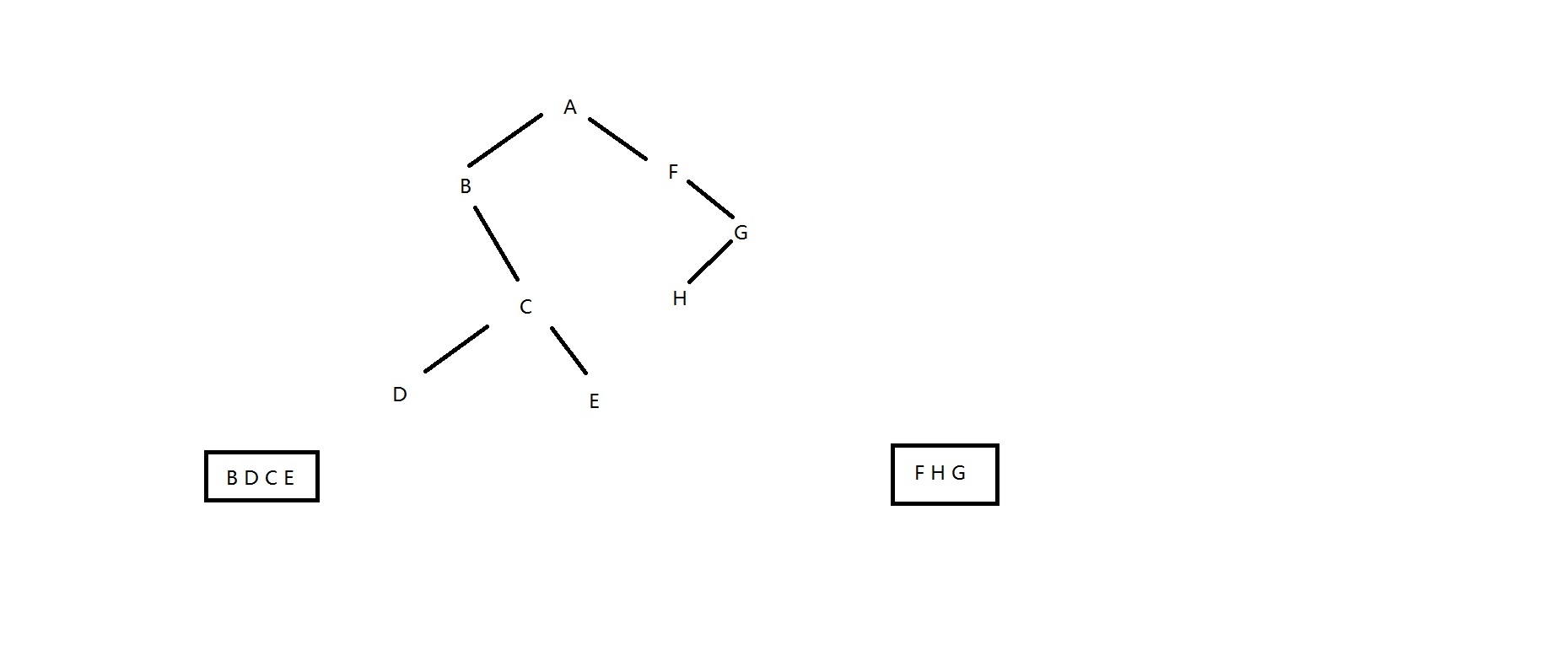
因此可以得到一條定律:後序定根,中序分左右。
3、若已知中序和先序序列......
例:
已知中序遍歷:G D H B A E C I F
已知先序遍歷:A B D G H C E F I
結果:
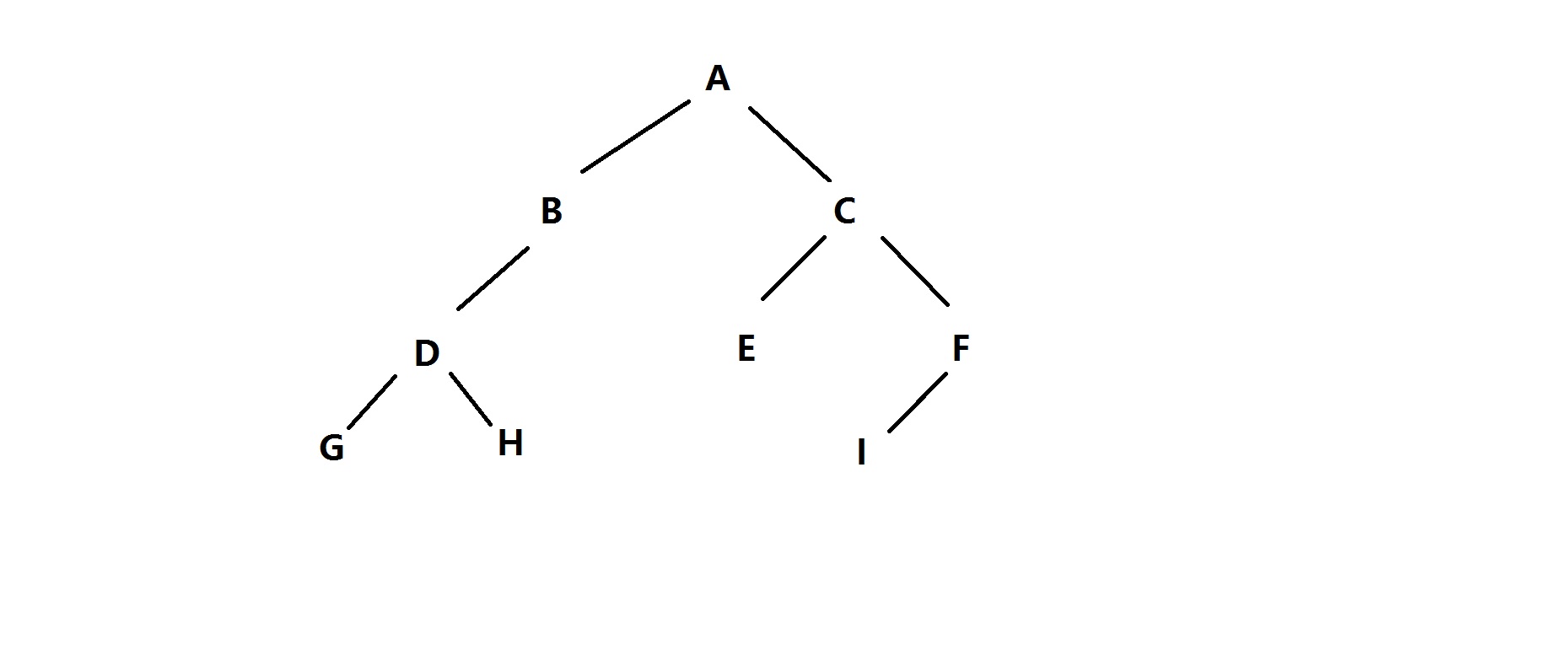
推斷過程:
類似上面的運用兩種遍歷方法的性質和遍歷表的排布,我就懶得寫了,推一推就出來了...
4、若已知先序和後序序列......
例:
二叉樹前序遍歷為ABDEGCFH,後序序列為DGEBHFCA
可以確定第一個根節點是A,A第一個子樹根節點是B,根節點為B的子樹後序遍歷為DGEB,前序遍歷為BDEG,A第二個子樹根節點為C,他的後序遍歷為HFC,前序遍歷為CFH,然後一次遞迴。簡單起見,我們只看A第二個子樹,即右子樹C。C的第一個根節點F,子樹F的後序遍歷HF,前序遍歷FH,C沒有第二個子樹,這時不管F為左子樹還是右子樹都是滿足要求的。同理F的子樹H。

圖中只有一個子樹的用兩條線連線,表示這是左右子樹均可。
最後結論:中序+先序,或中序+後序均能唯一確定一棵二叉樹,但先序+後序卻不一定能唯一確定一棵二叉樹。