20162317 2017-2018-1 《程式設計與資料結構》第七週學習總結
教材學習內容總結
- 1、樹:非線性集合
- 2、樹中包含的結構以及這些結構的定義
- 3、樹分類的依據
- 4、遍歷樹的方法以及分析
5、用連結串列以及陣列實現二叉樹
教材學習中的問題和解決過程
問題1:先序、中序、後序遍歷邏輯上的遍歷仍然學不通透,因此下面找三個樹圖來練習三種遍歷方法:
題目1:
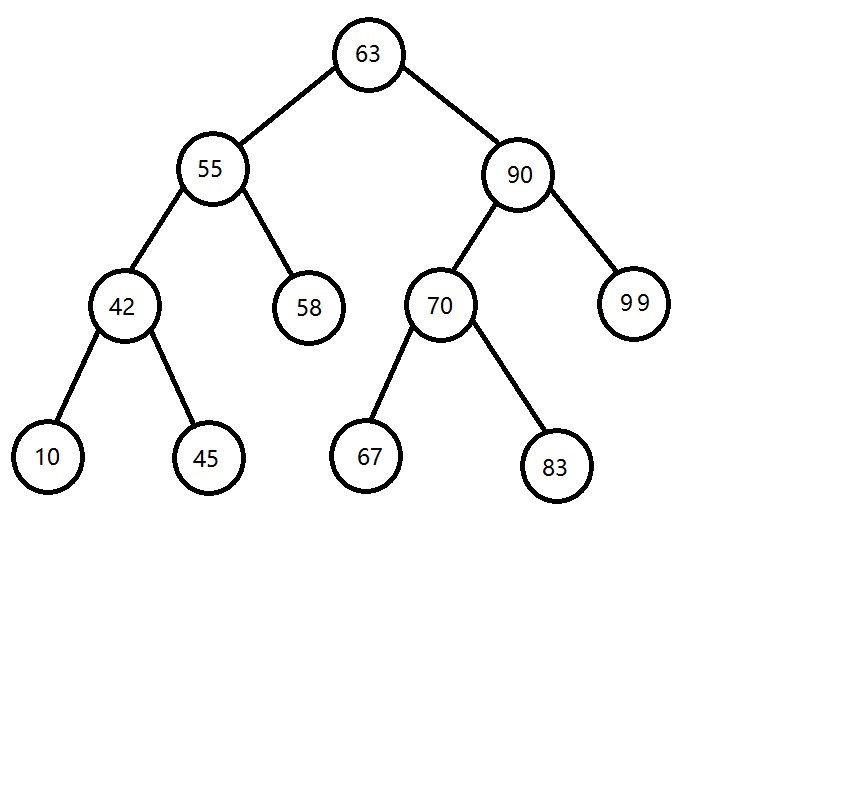
先序:63-55-42-10-45-58-90-70-67-83-99
中序:10-42-45-55-58-63-67-70-83-90-99
後序:10-45-42-58-55-67-83-70-99-90-63
題目2:
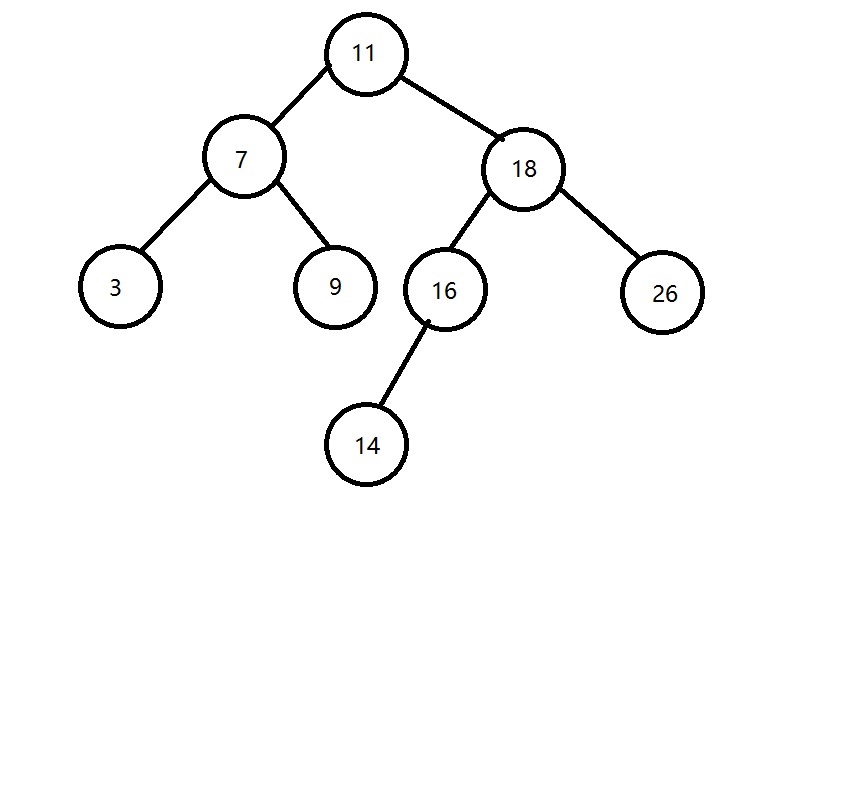
先序:11-7-3-9-18-16-14-26
中序:3-7-9-11-14-16-18-26
後序:3-9-7-14-16-26-18-11
題目3:
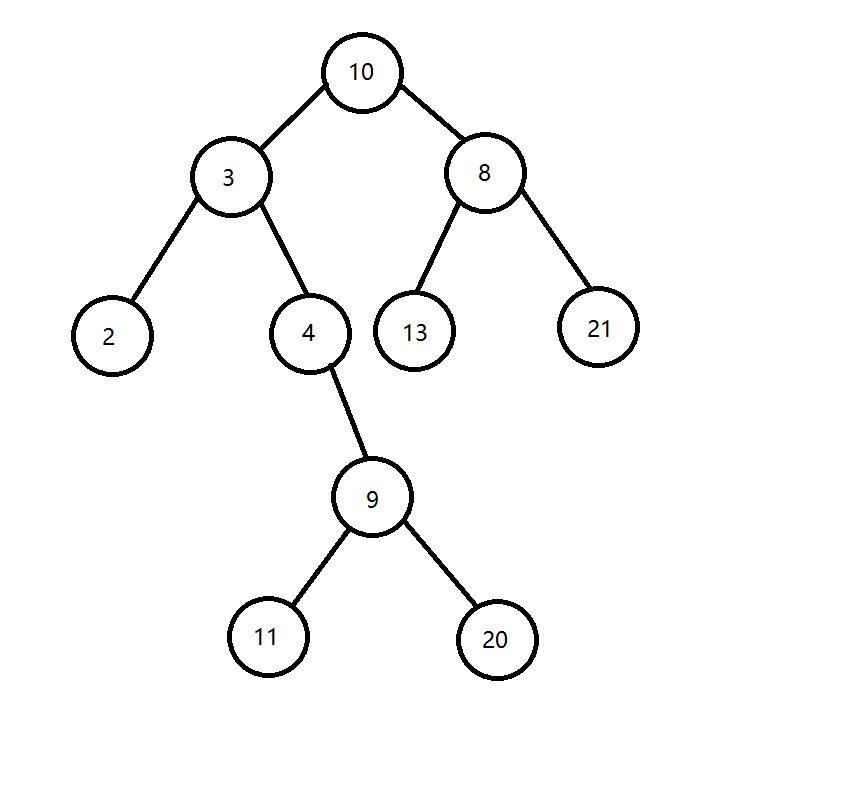
先序:10-3-2-4-9-11-20-8-13-21
中序:2-3-4-11-9-20-10-13-8-21
後序:2-11-20-9-4-3-13-21-8-10
問題2:有100個結點的完全二叉樹,其高度是多少?葉結點數是多少?
問題2解決方案:
高度:由二叉樹的性質可以指導,高度等於[log2n]+1,100個結點的話就可以得到[log2 100]+1,取整計算後得到答案是7。
葉結點:設葉結點的個數為n0度為2的結點數有n2個,則有n0 = n2+1,設完全二叉樹中度為1的結點數為n1個,n1為1或0,因此就有n0+n1+n2=100, 得到:n0+n1+n0-1=100, 2*n0 + n1 = 101,從此可看出,n1不能為0,必為1,從而得到2xn0=100,n0=50.所以葉結點有50個。
問題3:高度為h的完全二叉樹至少有多少個結點?至多有多少個結點?
問題3的解決方案:
- 至多的結點數:這個比較簡單,根據公式:2^h-1即這種情況,即倒數第二層的最後一個結點連著一個葉結點的情況。
-至少的結點數:倒數第二行第一個結點並沒有連著結點即可,即2^(h-1)個結點
問題4:已經知道一棵度為m的樹中有n1個度為1的結點,n2個度為2的結點,...,nm個度為m的結點,問該樹中有多少個葉結點?
問題4的解決方案:根據和同學的討論以及和網上資料的查閱:
設n為總結點個數,n0為葉子結點(即度為0的結點個數),則有:
n=n0+n1+n2+…+nm (1)
又有(分支總數):n-1=n11+n22+n33+…+nmm (2)
(因為一個結點對應一個分支)
式(2)-(1)得:
1=n0-n2-2n3-…-(m-1)nm
則有:n0=1+n2+2n3+…+(m-1)nm
問題5以及解決方案:對二叉樹遍歷操作的深入思考
程式碼託管
學習進度條
| 程式碼行數(新增/累積) | 部落格量(新增/累積) | 學習時間(新增/累積) | ||
|---|---|---|---|---|
| 目標 | 5000行 | 15篇 | 400小時 | |
| 第一週 | 200/200 | 2/2 | 20/20 | |
| 第二週 | 20/220 | 1/3 | 20/40 | |
| 第三週 | 645/865 | 1/4 | 14/54 | |
| 第五週 | 654/1519 | 1/5 | 18/72 | |
| 第六週 | 436/1955 | 1/6 | 16/88 | |
| 第七週 | 839/2794 | 2/8 | 20/108 |
計劃學習時間:18小時
實際學習時間:20小時
改進情況:遇到不會的問題會做一定的深究,要求自身對基礎更為紮實。