Mnist是針對小影像塊處理的,這篇講的是針對大影像進行處理的。兩者在這的區別還是很明顯的,小影像(如8*8,MINIST的28*28)可以採用全連線的方式(即輸入層和隱含層直接相連)。但是大影像,這個將會變得很耗時:比如96*96的影像,若採用全連線方式,需要96*96個輸入單元,然後如果要訓練100個特徵,只這一層就需要96*96*100個引數(W,b),訓練時間將是前面的幾百或者上萬倍。所以這裡用到了部分聯通網路。對於影像來說,每個隱含單元僅僅連線輸入影像的一小片相鄰區域。
卷積層:
自然影像有其固有特性,也就是說,影像的一部分的統計特性與其他部分是一樣的。這也意味著我們在這一部分學習的特徵也能用在另一部分上,所以對於這個影像上的所有位置,我們都能使用同樣的學習特徵。
對於影像,當從一個大尺寸影像中隨機選取一小塊,比如說8x8作為樣本,並且從這個小塊樣本中學習到了一些特徵,這時我們可以把從這個8x8樣本中學習到的特徵作為探測器,應用到這個影像的任意地方中去。特別是,我們可以用從8x8樣本中所學習到的特徵跟原本的大尺寸影像作卷積,從而對這個大尺寸影像上的任一位置獲得一個不同特徵的啟用值。
看下面例子容易理解:
假設你已經從一個96x96的影像中學習到了它的一個8x8的樣本所具有的特徵,假設這是由有100個隱含單元的自編碼完成的。為了得到卷積特徵,需要對96x96的影像的每個8x8的小塊影像區域都進行卷積運算。也就是說,抽取8x8的小塊區域,並且從起始座標開始依次標記為(1,1),(1,2),...,一直到(89,89),然後對抽取的區域逐個執行訓練過的稀疏自編碼來得到特徵的啟用值。在這個例子裡,顯然可以得到100個集合,每個集合含有89x89個卷積特徵。
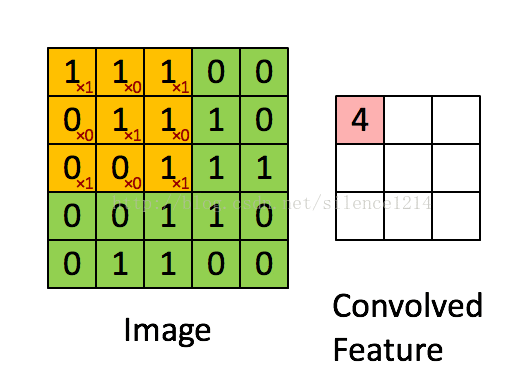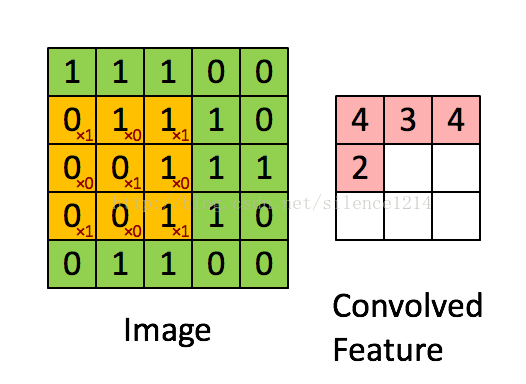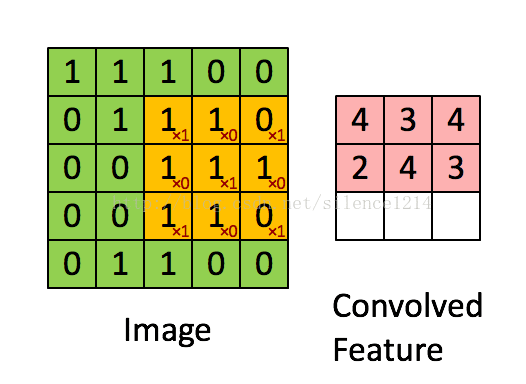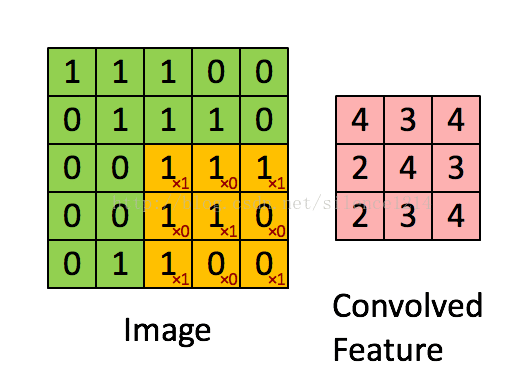
最後,總結下convolution的處理過程:
假設給定了r * c的大尺寸影像,將其定義為xlarge。首先透過從大尺寸影像中抽取的a * b的小尺寸影像樣本xsmall訓練稀疏自編碼,得到了k個特徵(k為隱含層神經元數量),然後對於xlarge中的每個a*b大小的塊,求啟用值fs,然後對這些fs進行卷積。這樣得到(r-a+1)*(c-b+1)*k個卷積後的特徵矩陣。
池化層:
在透過卷積獲得了特徵(features)之後,下一步我們希望利用這些特徵去做分類。理論上講,人們可以把所有解析出來的特徵關聯到一個分類器,例如softmax分類器,但計算量非常大。例如:對於一個96X96畫素的影像,假設我們已經透過8X8個輸入學習得到了400個特徵。而每一個卷積都會得到一個(96 − 8 + 1) * (96 − 8 + 1) = 7921的結果集,由於已經得到了400個特徵,所以對於每個樣例(example)結果集的大小就將達到892 * 400 = 3,168,400 個特徵。這樣學習一個擁有超過3百萬特徵的輸入的分類器是相當不明智的,並且極易出現過度擬合(over-fitting).
所以就有了pooling這個方法,翻譯作“池化”?感覺pooling這個英語單詞還是挺形象的,翻譯“作池”化就沒那麼形象了。其實也就是把特徵影像區域的一部分求個均值或者最大值,用來代表這部分割槽域。如果是求均值就是mean pooling,求最大值就是max pooling。
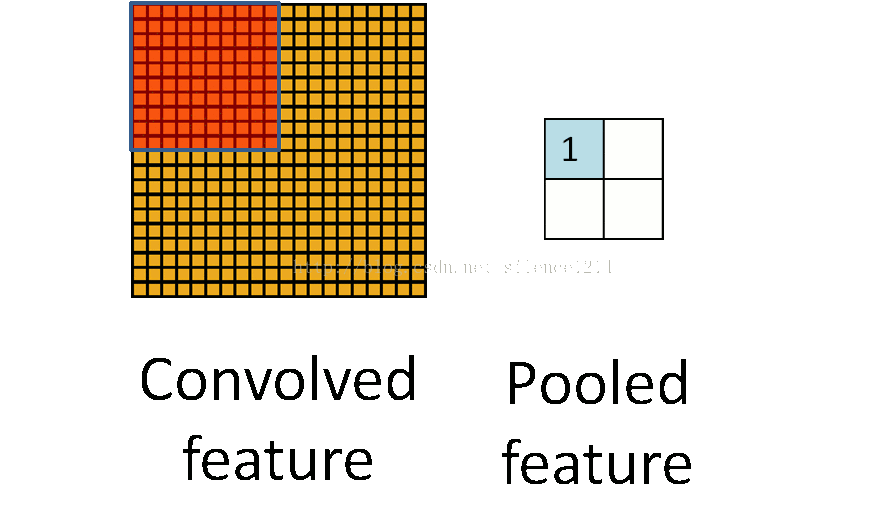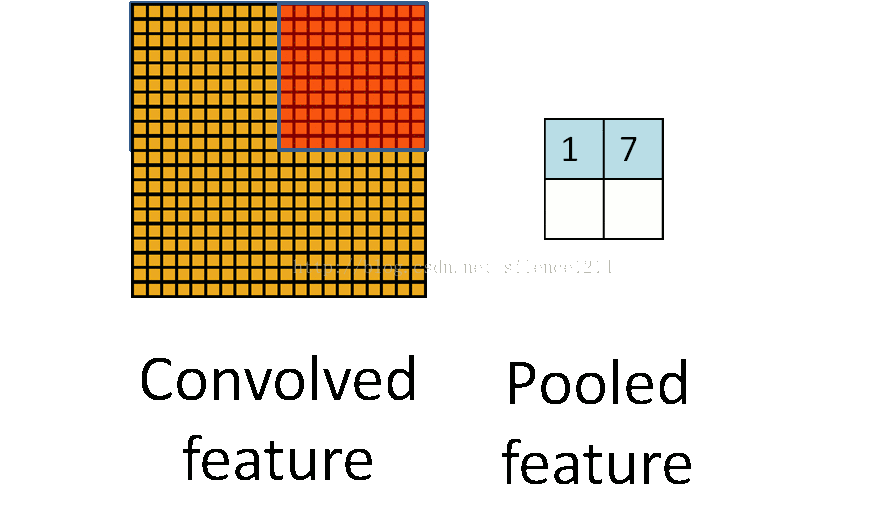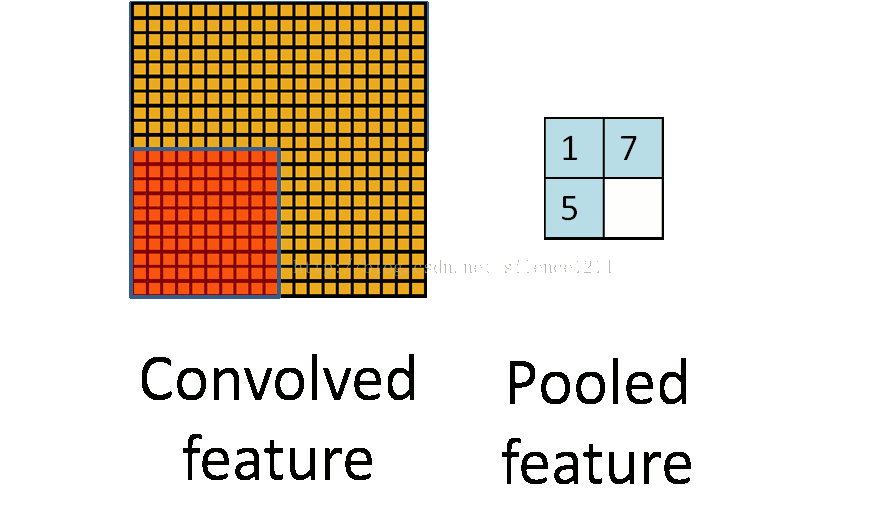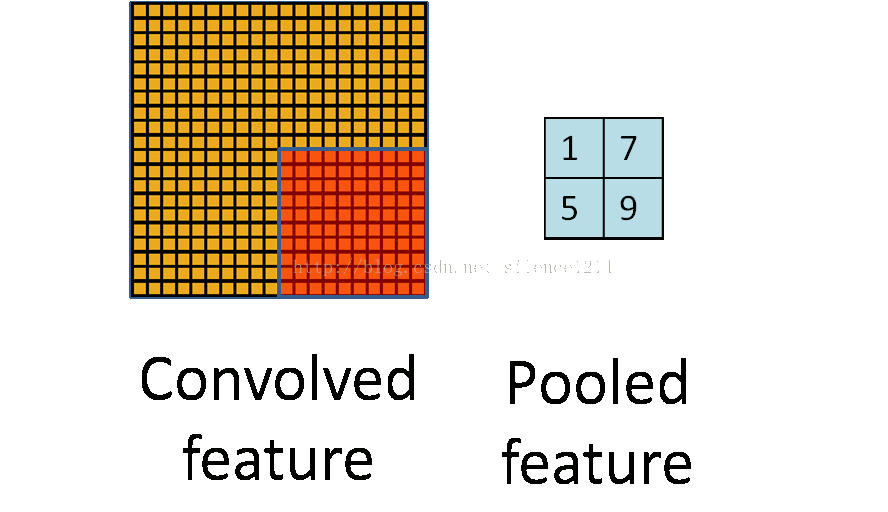
至於pooling為什麼可以這樣做,是因為:我們之所以決定使用卷積後的特徵是因為影像具有一種“靜態性”的屬性,這也就意味著在一個影像區域有用的特徵極有可能在另一個區域同樣適用。因此,為了描述大的影像,一個很自然的想法就是對不同位置的特徵進行聚合統計。這個均值或者最大值就是一種聚合統計的方法。
另外,如果人們選擇影像中的連續範圍作為池化區域,並且只是池化相同(重複)的隱藏單元產生的特徵,那麼,這些池化單元就具有平移不變性(translation invariant)。這就意味著即使影像經歷了一個小的平移之後,依然會產生相同的(池化的)特徵(這裡有個小小的疑問,既然這樣,是不是隻能保證在池化大小的這塊區域內具有平移不變性?)。在很多工中(例如物體檢測、聲音識別),我們都更希望得到具有平移不變性的特徵,因為即使影像經過了平移,樣例(影像)的標記仍然保持不變。例如,如果你處理一個MNIST資料集的數字,把它向左側或右側平移,那麼不論最終的位置在哪裡,你都會期望你的分類器仍然能夠精確地將其分類為相同的數字。