
Mozilla開發者社群是我學習的重要途徑,有一次逛到這個API看到Polyfill有幾行程式碼:
var list = Object(this); var length = list.length >>> 0;由於非CS的某野生專業出身,我對位運算子的瞭解比較模糊,大概能明白的只是list.length >>> 0對list.length做無符號右移,而返回值是>=0的整數,但背後的運算過程,就不能說得清楚了。複習了一下相關知識,做個筆記。
今天討論什麼?
本文,將嘗試從現代計算機中對數字的儲存和計算討論起,這也註定,雖然題目叫”Numbers in JavaScript”,但是大量篇幅應該集中在程式語言中主要使用的數字處理的方式。萬變不離其宗,懂了原理之後,對掌握各種語言圍繞同樣原理構建的Number也就輕鬆多了。當然,這其中就包括JavaScript。
先想幾個問題吧:
- JavaScript的數字為什麼有0和-0?
- JavaScript中的NaN為什麼互不相等?
- JavaScript中的數字真的只有一種型別嗎?
- JavaScript中常被詬病的0.3 - 0.2 == 0.1原因是什麼?
- 陣列的最大長度是多少?為什麼是這個值?
- 上述問題,只有在JavaScript中有嗎?
從硬體的角度上講,維護兩個狀態是相對容易的,比如一個二極體的導通或者截止,一個電脈衝的高或者低,從而在實現積體電路時候可以更加簡單高效,所以計算機普遍使用0和1來儲存和計算。那麼,只有0和1,如何表示1234567890呢?這就涉及到機器碼和真值。
機器碼和真值
所謂機器碼是指,整數在計算機中二進位制形式。規則很簡單,機器碼的最高位(左第一位)表示數字的正負,0表示正數,1表示負數,其餘位按照進位制轉換的規則表示具體數字。
所謂真值是指,機器碼按照上述轉換規則還原的帶有正負的實際整數。
舉例而言,用8-bits表示一個整數,則十進位制的整數+6可表示為:00000110;十進位制的數字-5可表示為10000101。這裡說的+6和-5便是真值,而表示它們的二進位制數便是機器碼。再次注意,最高位只用於表示正負,比如10000101的真值是-5而非133,以及我們關於機器碼和真值的討論是基於整數範圍的,浮點數在計算機中的儲存方式與整數有很大差值,將另作討論。
有了機器碼,我們便可以在計算機中使用機器碼儲存和計算真值,那麼機器碼在計算機中是如何計算的呢?
原碼、反碼、補碼
機器碼分為多種,主要包括原碼、反碼、補碼、移碼等,今天我們主要總結一下前三個,而移碼非常簡單,且多用於比較,不做詳細說明。另外需要補充一點,我們在此區分機器碼的這麼多種形式,主要是針對的有符號數,而無符號數,不需要使用最高位來表示正負,也就不需要這麼多種編碼方式。
原碼:
最高位表示正負,其它位表示真值的絕對值。其中,最高位為0表示正數或者0,為1表示負數。
比如,同樣以8bits長度的數串表示+7的原碼為0000 0111,-7的原碼為10000111。以後,我們會這樣表示:
[+7] = [00000111]原 [-7] = [10000111]原很明顯,8-bits的原碼能記錄的範圍為:[-127,+127].
原碼的好處在於,易於理解,相對直觀,方便人腦識別和計算。
對於原碼,人腦使用,可以直接計算出其真值然後可以進行後續操作。但對於計算機,首先,因為最高位用於表示正負,所以不能直接參與運算,需要識別然後做特殊處理;其次,具體計算使用絕對值進行操作,所以兩個運算元正負的異同會影響操作符,比如兩個異號相加實際要做減法操作,甚至異號相減還需要判斷絕對值大小然後決定結果正負。如此,我們計算機的運算器設計將會變得異常複雜。下面,我們將瞭解如何使用反碼和補碼將符號位參與運算,從而使加減法統一簡單高效地處理,這也是反碼和補碼出現的原因。
反碼:
正數的反碼等於其原碼,而負數的反碼則是對其原碼進行符號位不變,其它位逐一取反的結果。
比如,同樣以8-bits長度的數串表示+7,那麼有如下:
[+7] = [00000111]原 = [00000111]反 [-7] = [10000111]原 = [11111000]反同樣,8-bits的反碼能記錄的範圍為:[-127,+127]。
在按位取反之後,我們可以有下面的操作:
2 - 3 = 2 + (-3) = [00000010]原 + [10000011]原 = [00000010]反 + [11111100]反 = [11111110]反 = [10000001]原 = -1上面,我們將減法通過反碼轉化為了加法,如此,我們的運算將會簡單很多,但是反碼的方式同樣存在一些問題:
3 - 3 = 3 + (-3) = [00000011]原 + [10000011]原 = [00000011]反 + [11111100]反 = [11111111]反 = [10000000]原 = -0出現了-0,這個值是沒有意義的。另外,按照反碼加法法則,如果最高位有進位,需要在最低位上+1,那麼會出現:
3 - 2 = 3 + (-2) = [00000011]原 + [10000010]原 = [00000011]反 + [11111101]反 (這裡最高位有進位,需要在最低位+1) = [00000001]反 = [00000001]原 = 1這種情況,又增加了反碼運算的複雜性,影響效率,為解決上面的問題,出現了補碼。
補碼:
正數的反碼等於其原碼,而負數的補碼則是對其反碼進行末位加1的結果。
比如,再同樣以8-bits長度的數串表示+7,那麼有如下:
[+7] = [00000111]原 = [00000111]反 = [00000111]補 [-7] = [10000111]原 = [11111000]反 = [11111001]補使用補碼,繼續做之前的操作:
2 - 3 = 2 + (-3) = [00000010]原 + [10000011]原 = [00000010]反 + [11111100]反 = [00000010]補 + [11111101]補 = [11111111]補 = [11111110]反 = [10000001]原 = -1那麼,如果是3-3呢?
3 - 3 = 3 + (-3) = [00000011]原 + [10000011]原 = [00000011]反 + [11111100]反 = [00000011]補 + [11111101]補 = [00000000]補 = [00000000]原 = 0是否還需要做額外的加法操作?
3 - 2 = 3 + (-2) = [00000011]原 + [10000010]原 = [00000011]反 + [11111101]反 = [00000011]補 + [11111110]補 = [00000001]補 = [00000001]原 = 1這樣,我們便可以完美的將減法統一到加法之上,而且不需要繁瑣的正負判斷,進位控制,甚至可以節約一個位置。那麼,這個位置,也就是10000000如何處理呢?按照規定,10000000用來表示-128,正數的補碼/反碼/原碼相同,而負數的補碼只是佔用了-0的[10000000]原和[11111111]反轉換後得到的[10000000]補表示-128,但是這個只是幫助理解,不能反向回推得到-128的原碼和補碼。
所以,8bits的補碼能記錄的範圍為:[-128,+127]。
至此,我們已經瞭解了,計算機中主要使用的儲存和計算整數的方式,鑑於現代計算機主要使用補碼方式,自然能很容易理解各種數字型別的表示範圍,比如32bits的int範圍為:[-231,231-1]。這對於我們後面理解一些JavaScript中的極端情況至關重要。
稍加補充:
我們可能會想,原碼很容易接受的,可是反碼和補碼的出現是基於什麼樣的邏輯或者數學原理呢?這裡,我們可以蜻蜓點水地討論一下,因為這個tread已經超出今天話題有點多了。
常用來說明這個原理的例子是時鐘,時鐘的一週有12個數字,那麼,如果我們希望從3調整到8該如何操作?可以往前+5,也可以往後-7。這裡的兩個數字,+5和-7存在著的關係:它們同時對數字12求餘數得到同樣的結果。嚴格的概念是我們小時候學習的同餘,準確的描述上面的關係是+5和-7對模12同餘,+5和-7是互補關係,互為補碼。我們可以看出,在模的數字範圍之內,我們減去一個數字,恰好等於加上這個數字的補碼然後取餘。大致就這麼描述一下,詳細的過程是需要嚴謹的科學證明,網上有大量的文獻,在此我們適時收住點到為止,有興趣的同學自行google吧。
IEEE 754標準
作為一個JavaScript程式設計師,我們只有一個Number,所以我們從一開始就習慣了:
var num1 = 123; var num2 = 1.23;但是,你知道JS的number是IEEE 754標準的64-bits的雙精度數值嗎?這是一個什麼樣的標準?使用這個標準的64-bits雙精度意味著什麼?所以,要掌握JavaScript中的數字,我們首先得了解IEEE 754標準。下面,我將嘗試說明一下這個標準,為我們最後學習JavaScript中的數字做鋪墊。
標準的基本原理:
我們知道,對於計算機而言,數字沒有小數和整數的差別,也就是計算機中沒有小數點的存在。通過前文的討論,我們已經找到了很完美的整數儲存計算的方案,但是當涉及到小數,我們很容易發現,現有的方案無法解決我們的需求。然後,電腦科學家們便嘗試了多種方案,主要便是定點數和浮點數兩種。
所謂定點數,是指小數點位置固定在數串中間的某個特定位置,點兩側分別為數字的整數和小數部分。比如用8-bits字長的數串,小數點固定在正中間位置,那麼11001001和00110101分別表示1100.1001和11.0101兩個數字。這種方案簡單直觀易理解,但是存在嚴重的空間浪費,以及容易溢位的問題。
所謂浮點數,是指小數點的位置是不固定的,通過科學計數法(這個應該不需要解釋吧)的方式控制小數點的位置,表示不同的數字。這個表示方案便是IEEE 754標準使用的方案。IEEE 754標準是目前使用最廣泛的浮點數運算標準。下面我們將主要討論一下此方案。
現在,讓我們想一下小時候學習的科學計數法,比如-123.456這個數字,轉換成科學計數法應該是:-1.23456 × 10^2。這裡面已經包含了IEEE 754標準的主要元素。我們梳理一下:第一個,自然是正負號的問題,需要一個標誌;然後,需要一個具體的數字,表示有效數字或者精度,如上例的1.23456;再然後,需要一個控制小數點位置的數字,如上例的10^2,回憶一下,我們學習科學計數法的時候,要求前面的數字的絕對值大於1而小於10,也就是小於10^2中的底數(Base),進位制固定之後,底數應該是固定的,所以這裡起決定作用的是指數,也就是上例中的2。那麼,有了這三個元素,我們便可以很輕鬆的表示出一個數字,並且靈活的調節小數點位置從而控制數字正負、精度和大小。
上面的要素,轉換成標準語言描述,我們稱表示正負的標誌叫符號(Sign),表示精度的數字為尾數(Mantissa)或者有效數字(Significand),而控制小數點位置的指數就叫指數(Exponent),指數和基數(Base)共同作用參與計算。下圖取自wikipedia,我們直觀地感受下這三個要素在一個數串中的相對關係(fraction區域即等同於前面說的有效數字區域):

瞭解最基本的原理後,我們來大致看一下IEEE 754標準做了什麼。
首先做的事情就是規定這三個要素在一個數串中佔有的位數,試想一下,如果各個實現的位數不確定,那麼我們是不是很難正確的還原出原始數字?IEEE 754標準規定了四種表示浮點數值的方式:單精確度(32位)、雙精確度(64位)、延伸單精確度(43位元以上,很少使用)與延伸雙精確度(79位元以上,通常以80位元實做)。只有32位模式有強制要求,其他都是選擇性的。而現在主流的語言,多提供了單精度和雙精度的實現,我們在此主要比較一下這兩者,如圖是它們各個部分對應上圖,所使用的位數如下:
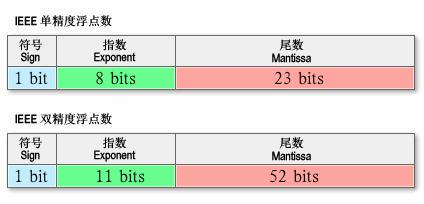
補充一點的是,無論是科學計數法還是標準的規定,都要求有效數字(不考慮符號位)必須>=1&&<Base。所以,有效數字其實是一個定點數,小數點的位置固定在有效數字域的最高位和次高位之間。那麼,按照上述規定,在二進位制中,最高位只能是1,所以標準要求省略其最高位,於是精度提高一位。比如,32-bits的單精度有效數字區域只有23位,但是精度卻是24位;64-bits的雙精度,擁有52位的有效數字域卻是54位精度的。
然後,還有一個問題,如果按照先有的約定,是不是無法表示小於1的實數?因為,指數一定>=0,有效數字一定>1。於是,IEEE 754標準提出了一個很重要的指數偏移值。它是說明指數域(Exponent佔用的區域)的編碼值為指數的實際值加上某個固定的值,換言之便是,如果我們根據指數域計算出的指數是N,那麼參與計算實際浮點數的指數應該是N-指數偏移值。根據IEEE 754標準的規定,該固定值為2^(e-1) - 1,其中的e為儲存指數的位元的長度。比如,從上圖中我們看到,32-bits的單精度是以8-bits表示一個指數域,那麼偏移值應該是2^(8-1) - 1 = 128−1 = 127。所以,容易得出,單精度浮點數的指數部分實際取值是[-127,128]。比如,某個32-bits單精度的指數為十進位制的1,那麼指數域的編碼應該是10000001,某個32-bits單精度的指數域編碼是00000001,那麼該指數的實際值應該是十進位制的-126。這樣,我們就能通過偏移值將正指數轉換為負指數,從而使浮點數能逼近0。浮點數的指數計算跟前面討論的機器碼恰好相反,正數的最高位都是1,而負數的最高位都是0。
以上的描述,便是IEEE 754標準最需要我們瞭解的原理部分,但是,作為一個廣泛使用的工業標準,規定這些還是遠遠不夠的。
稍加補充:
wikipedia對IEEE 754標準有如下描述:
這個標準定義了表示浮點數的格式(包括負零-0)與反常值(denormal number)),一些特殊數值(無窮(Inf)與非數值(NaN)),以及這些數值的“浮點數運算子”;它也指明瞭四種數值舍入規則和五種例外狀況(包括例外發生的時機與處理方式)。下面,補充幾個,我認為與本文後續討論相關的或者可以幫助大家理解極端現象的定義:
規約形式的浮點數:如果浮點數中指數部分的編碼值在0 < exponent < 2^(e-1)之間,且尾數部分最高有效位(即整數字)是1,那麼這個浮點數將被稱為規約形式的浮點數。也就是,嚴格按照我們上文描述編碼的數字。
非規約形式的浮點數:如果浮點數的指數部分的編碼值是0,尾數為非零,那麼這個浮點數將被稱為非規約形式的浮點數。IEEE 754標準規定:非規約形式的浮點數的指數偏移值比規約形式的浮點數的指數偏移值大1.例如,最小的規約形式的單精度浮點數的指數部分編碼值為1,指數的實際值為-126;而非規約的單精度浮點數的指數域編碼值為0,對應的指數實際值也是-126而不是-127。實際上非規約形式的浮點數仍然是有效可以使用的,只是它們的絕對值已經小於所有的規約浮點數的絕對值;即所有的非規約浮點數比規約浮點數更接近0。規約浮點數的尾數大於等於1且小於2,而非規約浮點數的尾數小於1且大於0.
上面的兩個概念,幾乎是直接從wikipedia上扒下來的,非規約形式的浮點數出現的意義是避免突然式下溢位(abrupt underflow),而採用漸進式下溢位。這已經是上世紀70年代的事情了,差不多是我的年齡的兩倍了。這個是一些非常極端的情況,在此我嘗試最簡單地描述一下非規約形式的浮點數出現的意義,知道有這麼回事便可:下面,以單精度為例,如果沒有非規約形式的浮點數,那麼絕對值最小的兩個相鄰的浮點數之間的差值將是絕對值最小的浮點數的2^23分之一,大家想一下,絕對值次小的浮點數減去絕對值最小的浮點數的值是多少?
1.00...01 × 2^(-126) - 1.00...00 × 2^(-126) = 0.00..01 × 2^(-126) = 1 × 2^(-126-23) = 2^(-149)很明顯,絕對值最小的規約數無法表達其和次小的規約數的差值,所以很容易導致有若干數字之間的差值下溢,可能會觸發意料之外的後果。而如果採用非規約形式的浮點數,指數全0,偏移值比規約數偏移值大1(-126比-127大1),尾數小於1,那麼非規約數能表達的最小值便是:
0.00..01 × 2^(-126) = 1 × 2^(-126-23) = 2^(-149)所以,非規約形式的浮點數解決了前述的突然式下溢位(abrupt underflow)而被標準採納。
IEEE 754標準還規定了三個特殊值:
- 指數全0且尾數小數部分全0,則這個數字為±0。(符號位決定正負)
- 指數為2e – 1且尾數的小數部分全0,這個數字是±∞。(符號位決定正負)
- 指數為2e – 1且尾數的小數部分非0,這個數字是NaN。
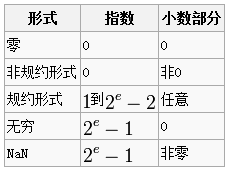
現在,讓我們回憶一下,各種語言中普遍描述的雙精度浮點數的範圍:[-1.7 × 10-308,1.7 × 10308]。打個岔,想象一個有300多位的十進位制數字的適用情形,私以為遠超過普通人想象力的邊界。這個範圍為什麼是這個範圍呢?我覺得,通過上面的討論,大家應該能清晰,1.7/308這些數字出現的必然原因。
首先,我們應該很容易根據偏移量得出雙精度浮點數的計算公式:
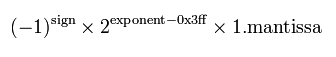
然後,以正數為例,按照上述特殊值中±∞和NaN的約定,指數的最大值應該滿足指數取規約數的指數範圍的最大值,然後小數部分取小數部分的最大值,可以得出這個二進位制的數字應該是:
0 11111111110 11..11(52個)轉換為16進製表示:
0x7fef ffff ffff ffff那麼,根據前述規約數的原理,反編碼便得到十進位制的:1.7976931348623157 x 10^308。類似的道理,Sign位取反,便是範圍的下限。
到此為止吧,我對IEEE 754標準也是最近幾天稍加學習,再說多了就誤導大家了。通過這幾天的學習,我感覺,我們在理解的IEEE 754標準及浮點數的時候,要特別注意將精度和範圍兩個概念分別開來。範圍只是一個模糊的界限,精度才是能準確表達的數字。
回到JavaScript
在上面的討論中,我們很少提及JavaScript,似乎有點背離今天的主題了,但是,在瞭解了前述的原理之後,我們對JavaScript中數字的把握將”水到渠成”。這終將是一次,鋪墊多於正文,開胃菜多於正餐的討論。嗯,快喊小夥伴,正餐開始了!
ES的”The Number Type”:
現在,我們開啟ES規範的“The Number Type”是不是基本通讀下來了?
比如:
The Number type has exactly 18437736874454810627 (that is, 264 − 253 + 3) values…為什麼是這個數字?因為,我們說JavaScript中的數字是64-bits的雙精度,所以首先有2^64中可能的組合,然後,按照前述的IEEE 754標準的標準中的特殊值中的部分,NaN和±∞佔用了2^53個數值,但是表示了三個直觀的量,所以,加減一下,自然就是18437736874454810627 (that is, 2^64 − 2^53 + 3) values。
…the 9007199254740990 (that is, 253−2) distinct “Not-a-Number” values…為什麼這麼多NaN?同樣,按照前述的IEEE 754標準的標準中的特殊值中的部分,NaN使用了Significand非零、指數是特定2^e-1且Sign無要求的所有可能,即2^53減去±∞兩種情況。
…e is an integer ranging from −1074 to 971…為什麼指數的範圍是這個呢?而不是-1022到+1022呢?因為,ES演化了一下公式,對比一下我們之前演示64-bits的公式,關於參與計算的mantissa,我們按照IEEE 754標準在演示的時候中使用的是1.m,而ES規範中使用的是m,當然會有尾數域bit長度的差異了。
到這裡,關於數字,大概就可以結束了。開篇的幾個問題,相信讀到這裡的同學,都能有答案了。但是,還有一個問題,JavaScript中的數字真的只有一種型別嗎?,而且貌似到現在與我們的初衷,理解>>>有點偏離了。不過,世界上很多事情往往都是這樣,解釋原理需要到口乾舌燥,而用原理去解釋現象卻只需要三言兩語。
JavaScript不是隻有64-bits的雙精度
是的,小標題已經回答了我們的問題,JavaScript不是隻有64-bits的雙精度。我們通篇都在說JavaScript中數字的各種,一直按照64-bits的雙精度來描述,但是,如之前所說,ES中有ToInteger/ToInt32/ToUint32/ToUint16等Type Conversion。這些Type Conversion不是我們直接呼叫的API,而是語言引擎在進行某些特定操作的時候,替我們做的。這種“隱形的操作”,只有在一些極端的情況下,會表現出來。現在,我們可以到“ToInt32”/“ToUint32”/“ToInt16”三個地方看一下,稍作比較便能發現,他們的差異很小,只是在特定的步驟中存在差異。比如,ToUint32和ToUint16的差異僅僅操作的最後一步存在差異,按順序列出比較一下:
Let int32bit be posInt modulo 232; that is, a finite integer value k of Number type with positive sign and less than 232 in magnitude such that the mathematical difference of posInt and k is mathematically an integer multiple of 232.vs
Return int32bit.
Let int16bit be posInt modulo 216; that is, a finite integer value k of Number type with positive sign and less than 216 in magnitude such that the mathematical difference of posInt and k is mathematically an integer multiple of 216.比較一下,不難發現,僅僅是2^32和2^16的差異,而關鍵點恰是modulo操作的時候,按照我們之前討論的原理,很容易理解這個操作決定了可能出現的最大數。這樣的比較,有一好處,能提高我們閱讀標準的速度,而且加深理解,對掌握標準很有幫助。
Return int16bit.
總結一下這三個操作的範圍:
ToInt32的範圍便是其它強型別語言中的[-231, -231 – 1]。
ToUint32的範圍便是其它強型別語言中的[0, -232 – 1]。
ToUint16的範圍便是其它強型別語言中的[0, -216 – 1]。
通過搜尋,很容易能找到,JavaScript中那些操作中使用了上述相關的操作。其中,ToUint16僅僅在String.fromCharCode中有使用,我們不做討論了。ToInt32有在多個位運算子中使用,比如~/<</>>,以及在parseInt也有使用。而ToUint32的使用則出現在了大量的地方,主要分佈在,陣列相關的操作,位運算的操作兩個區域。
我們就借ToUint32的這些使用,回到開篇討論的那個地方吧:
首先,來到這裡>>>,看到操作如下:
1.Let lref be the result of evaluating ShiftExpression.再看new Array (len),有一句:
2.Let lval be GetValue(lref).
3.Let rref be the result of evaluating AdditiveExpression.
4.Let rval be GetValue(rref).
5.Let lnum be ToUint32(lval).
6.Let rnum be ToUint32(rval).
7.Let shiftCount be the result of masking out all but the least significant 5 bits of rnum, that is, compute rnum & 0x1F.
Return the result of performing a zero-filling right shift of lnum by shiftCount bits. Vacated bits are filled with zero. The result is an unsigned 32-bit integer.
If the argument len is a Number and ToUint32(len) is equal to len, then the length property of the newly constructed object is set to ToUint32(len). If the argument len is a Number and ToUint32(len) is not equal to len, a RangeError exception is thrown.對比不難發現,>>>的返回值和array.length的取值範圍,無差異,經過>>>操作後的數字,一定是一個合法的array.length。解釋原理總是那麼複雜,可是用原理解釋現象總是那麼簡單。
來自:程式師
評論(4)