近期工作中要處理很多 SVG 圖片, 所以從零開始學習了 SVG 的相關內容.
我看的是這本書 SVG Essentials, 2nd Edition,以及它的中譯版 SVG精髓(第2版).
這本書深入淺出, 例子很多, 非常不錯. 因為 svg 涉及到很多關於顏色的內容, 所以還是建議大家看電子版.
工作中的任務是實現一個相框功能, 當中涉及到了諸如 use, image, clip-path 的內容, 學習了一段時間後總算解決了, 所以希望記錄一下學習內容和解決方案.
內容比較多, 所以準備開一個系列, 這是 SVG 系列的第一篇, 基礎知識總結. 後續將會有更多關於 SVG 的內容. 敬請期待!
SVG basics
Shape Reference Summary
| 形狀 | 描述 |
|---|---|
<line x1="start-x" y1="start-y" x2="end-x" y2="end-y"/> |
直線: 起點(start-x, start-y) 終點(end-x, end-y); |
<rect x="left-x" y="top-y" width="width" height="height" /> |
矩形: 左上角(left-x, top-y), 寬高 width, height |
<circle cx="center-x" cy="center-y" r="radius"/> |
圓: 圓心(center-x, center-y) 半徑 r |
<ellipse cx="center-x" cy="center-y" rx="x-radius" ry="y-radius"/> |
橢圓: 圓心(center-x, center-y) xy軸半徑 rx, ry |
<polygon points="points-list"/> |
多邊形: 由一系列座標組成, points-list: x1 y1 x2 y2 x3 y3 .... |
<polyline points="points-list"/> |
折線: 由一系列座標組成, points-list: x1 y1 x2 y2 x3 y3 .... |
Path Reference Summary
本質上, 上述基本形狀都是路徑(path)的簡寫. 簡寫可以使得 svg 文件更具有可讀性. 但是當碰到複雜路徑時, 就需要 path 來描述. 以下總結中, 凡是出現大寫字母表示後續座標為絕對座標, 凡是小寫字母都代表相對於上一個座標的相對位移. Z 同 z 無差別. 因為表示閉合, 其後不用跟座標
| command | 描述 |
|---|---|
M(m) x y |
移動到(x, y) (小寫表示相對於上個座標的位移, 下同) |
L(l) x y |
畫一條直線到(x, y) |
H(h) x |
水平畫一條直線到 x |
V(v) y |
豎直畫一條直線到 y |
A(a) rx ry x-axis-rotation large-arc sweep x y |
畫一段到(x,y)的橢圓弧. 橢圓弧的 x, y 軸半徑分別為 rx,ry. 橢圓相對於 x 軸旋轉 x-axis-rotation 度. large-arc=0表明弧線小於180讀, large-arc=1表示弧線大於180度. sweep=0表明弧線逆時針旋轉, sweep=1表明弧線順時間旋轉. 具體解釋看如何繪製橢圓弧 |
Q(q) cx cy x y |
從當前點畫一條到(x, y)的二次貝塞爾曲線, 曲線的控制點為(cx, cy). 關於二次貝塞爾曲線請看[二次貝塞爾曲線詳解](#articleHeader6 |
T(t) x y |
此命令只能跟在一個 Q 命令使用, 假設 Q 命令生成曲線 s, T 命令的作用是從 s 的終點再畫一條到(x y)的二次貝塞爾曲線, 曲線的控制點為 s 控制點關於 s 終點的對稱點. T 命令生成的曲線會非常平滑 |
C(c) cx1 cy1 cx2 cy2 x y |
從當前點畫一條到(x, y)的三次貝塞爾曲線, 曲線的開始控制點和終點控制點為別為 (cx1, cy1), (cx2, cy2). 關於三次貝塞爾曲線請看三次貝塞爾曲線詳解 |
S(s) cx2 cy2 x y |
此命令只能跟在 C 命令後使用, 假設 C 命令生成曲線 s, S 命令的作用是再畫一條到 (x, y)的三次貝塞爾曲線, 曲線的終點控制點是 (cx2, cy2), 曲線的開始控制點是 s 的終點控制點關於 s 終點的對稱點. |
Transformation Reference Summary
| transform | 描述 |
|---|---|
translate(x, y) |
平移: 將使用者座標系統的座標原點移動到(x, y) |
scale(xFactor, yFactor) |
縮放: 將使用者座標系統的xy軸單位長度分別乘(xFactor, yFactor)倍 |
scale(factor) |
縮放: 同 scale(factor, factor)
|
rotate(angle, centerX, centerY) |
旋轉: 將使用者座標系統以(centerX, centerY)為旋轉中心順時針旋轉 angle 度 |
rotate(angle) |
旋轉: 同 rotate(angle, 0, 0)
|
skewX(angle) |
傾斜: 根據 angle 傾斜所有 x 軸座標, 視覺上會看到 y 軸傾斜... |
skewY(angle) |
傾斜: 根據 angle 傾斜所有 y 軸座標, 視覺上會看到 x 軸傾斜... |
matrix(a b c d e f) |
矩陣變換: 將座標系統進行矩陣變換, 詳細內容請參考後續文章 |
Details
Ellipse
一種直觀的表示橢圓弧線的方式是, 根據橢圓中心 (x, y), x 軸半徑 rx, y 軸半徑 ry, 開始角度 startAngle, 結束角度 endAngle.
但是為什麼 SVG 會採用 A(a) rx ry x-axis-rotation large-arc sweep x y 這樣的形式呢,
主要是因為在 SVG 中, 弧線並不是孤立的存在, 他要成為整體的一部分. 所以 SVG 採用了起始點這樣的方式.
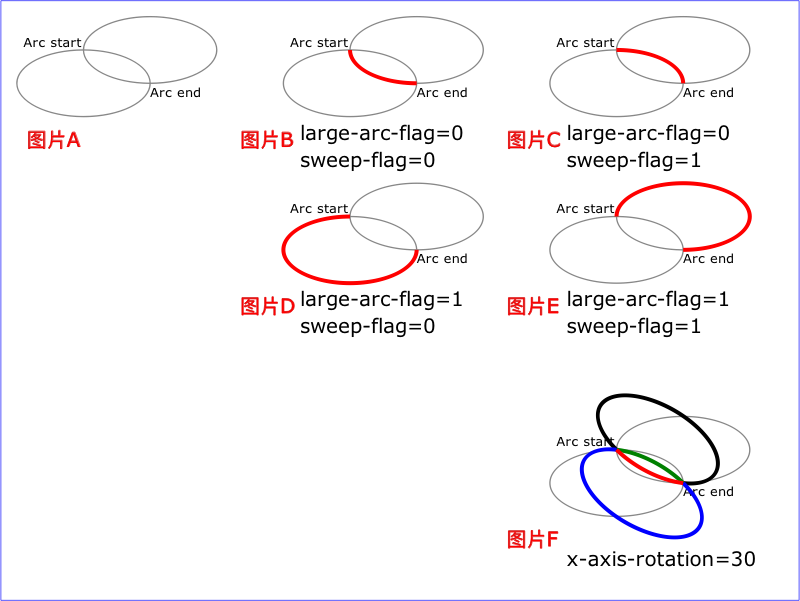
那麼其他的 x-axis-rotation, large-arc, sweep 又是什麼意思呢? 我們現在來看下面這張圖.
當確定了兩個點已經橢圓的 rx, ry 後並不能唯一確定一條橢圓弧, 實際上根據是否是大圓, 路徑是否是逆時針可以產生四條 (b, c, d, e)
其中, large-arc-flag=0 表示小圓, sweep-flag=0 表示逆時針.
那麼 x-axis-rotation 又是什麼意思呢? b, c, d, e 產生的前提是 橢圓的 x 軸與使用者座標系的 x 軸是平行的.
f 圖表示橢圓 x 軸相對於使用者座標系的 x 軸旋轉30度所產生的橢圓弧. 灰色的部分表示原來產生的橢圓弧.
Quadratic Bezier
關於貝塞爾曲線的數學含義請看Bézier curve
這裡直觀的講一下
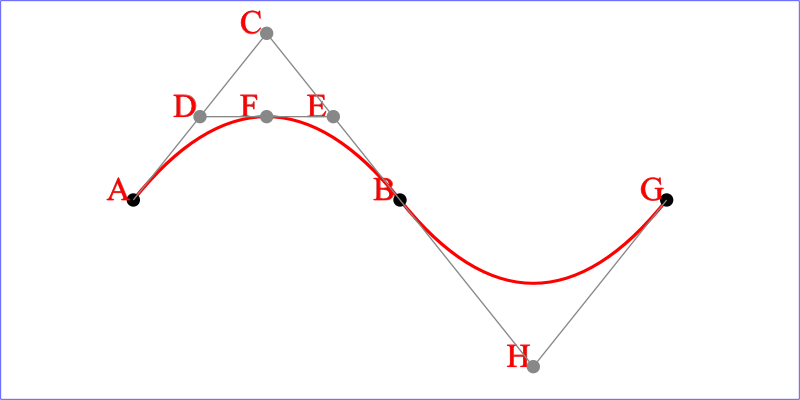
以上曲線的路徑表示是: <path d="M200,300 Q400,50 600,300 T1000,300"/>
我們可以看出:
A 是起點, B 是終點, C 就是控制點.
找出 AC 的重點 D, BC 的重點 E, 連線 DE, 找出其中點 F, F 即這條曲線前半段的一個切點.
這裡不談數學含義, 這樣的幾何意義更加直觀.
再來看 T 命令, 其實 T 命令是 Q 的一個簡寫.
其控制點 H 就是上個 Q 命令的控制點 C 關於終點 B 的對稱點.
使用 T 命令產生的曲線往往比較順滑 :)
Cubic Bezier
再來看一下三次貝塞爾曲線
<path d="M100,200 C100,100 250,100 250,200 S400,300 400,200"/>
前半段曲線(C 命令) s1:
起點 A, 終點 B, 起點控制點 C, 終點控制點 D, 連線 AC, BD, CD;
找到 CD 中點 F, 連線 AC 中點 E 與 F, 連線 BD 中點 G 與 F;
連線 EF, FG, 連線 EF 中點 H 與 FG 中點 I;
I 即為前半段曲線的切點;
後半段曲線(S 命令) s2:
S 只能跟在 C 命令後使用;
s2 的起點 B, 終點 L, 終點控制點 K;
s2 的起點控制點是 s1 的終點控制點 D 關於 s1終點 B 的對稱點
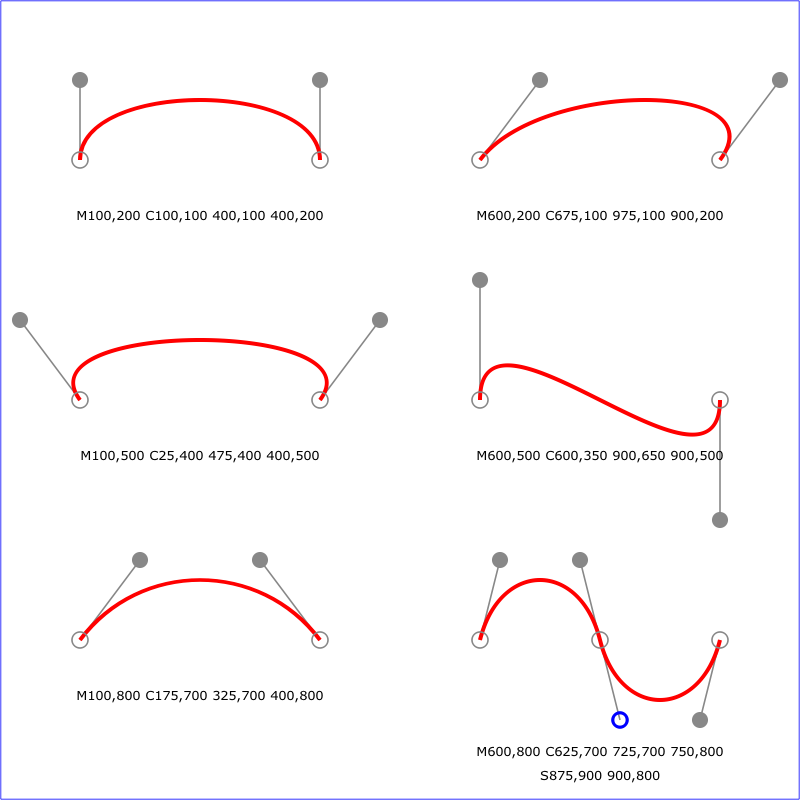
下圖是更多關於三次貝塞爾曲線的例子: