作者:Vamei 出處:http://www.cnblogs.com/vamei 歡迎轉載,也請保留這段宣告。謝謝!
前面介紹的分佈描述量,比如期望和方差,都是基於單一隨機變數的。現在考慮多個隨機變數的情況。我們使用聯合分佈來表示定義在同一個樣本空間的多個隨機變數的概率分佈。
聯合分佈中包含了相當豐富的資訊。比如從聯合分佈中抽取某個隨機變數的邊緣分佈,即獲得該隨機變數的分佈,並可以據此,獲得該隨機變數的期望和方差。這樣做是將視線限制在單一的一個隨機變數上,我們損失了聯合分佈中包含的其他有用資訊,比如不同隨機變數之間的互動關係。為了瞭解不同隨機變數之間的關係,需要求助其它的一些描述量。
協方差
協方差(covariance)表達了兩個隨機變數的協同變化關係。我們取一個樣本空間,即學生的體檢資料。學生的身高為隨機變數X,學生的體重為隨機變數Y。
| 160cm | 170cm | 180cm | |
| 60kg | 0.2 | 0.05 | 0.05 |
| 70kg | 0.05 | 0.3 | 0.05 |
| 80kg | 0.05 | 0.05 | 0.2 |
根據上表,大的身高(180cm)和大的體重(80kg)同時出現的概率較大(0.2),小的身高值(160cm)和小的體重(60kg)的概率也較大(0.2)。偏大的身高往往伴隨偏大的體重,偏小的身高常伴隨偏小的體重。這種“大”伴隨著“大”,“小”伴隨著“小”的情形,叫做正相關。根據上面的資料,身高和體重兩個隨機變數正相關性很強。
另一方面,如果“大”配“小”,“小”配“大”的概率很高,那麼兩個隨機變數負相關。“最萌身高差”是負相關的一個範例。(樣本空間為情侶的身高資訊。可以定義男生身高為一個隨機變數,女生身高為另一個隨機變數)

正如其他的分佈描述量一樣,協方差從概率分佈中提取資訊,讓我們獲知分佈的“效能”。對於一個已知的聯合分佈來說,任意兩個隨機變數之間都可以計算出一個協方差,即一個數值。
定義
協方差的定義如下,如果X和Y是聯合分佈的隨機變數,且分別有期望[$\mu_X$],[$\mu_Y$],那麼X和Y的協方差為
$$Cov(X, Y) = E[(X - \mu_X)(Y - \mu_Y)]$$
協方差的定義基於期望。根據期望的定義,協方差可以直接用於離散隨機變數和連續隨機變數。
我們已經知道,期望是某個隨機變數根據概率的加權平均。我們所要加權平均的目標是[$X - \mu_X$]和[$Y - \mu_Y$]的乘積。隨機變數和期望的差,代表了隨機變數的取值和中心值的偏離程度,也就是我們上面所謂的“偏大”或者“偏小”的情況:正值的偏離表示“偏大”,負值的偏離表示“偏小”。如果是正相關,即大配大,小配小的情況,那麼這一乘積為正;如果是負相關,乘積為負。所以,通過[$(X - \mu_X)(Y - \mu_Y)$]這個量,我們表達了X和Y的相關性。
回到剛才的資料來計算相關性,
| 160cm | 170cm | 180cm | |
| 60kg | 0.2 | 0.05 | 0.05 |
| 70kg | 0.05 | 0.3 | 0.05 |
| 80kg | 0.05 | 0.05 | 0.2 |
讓身高為X,體重為Y。我們可以通過邊緣分佈,來分別獲得X和Y的分佈(回憶一下)。求得X和Y的期望,分別為170和70。計算各個格子中的[$(X-\mu_X)(Y-\mu_Y)$]
| 160cm | 170cm | 180cm | |
| 60kg | 100 | 0 | -100 |
| 70kg | 0 | 0 | 0 |
| 80kg | -100 | 0 | 100 |
上面的兩個表,對應的格子相乘,並求和,就得到協方差:
$$\begin{align} Cov(X, Y) & = 0.2 \times 100 + 0.2 \times 100 + 0.05 \times (-100) + 0.05 \times (-100) \\ & = 30 \\ \end{align}$$
在上面的計算中,正相關的專案都分配有比較大的概率值。最終的協方差也是一個正值。
根據期望的性質,我們可以改寫協方差的表達形式:
$$\begin{align} Cov(X, Y) & = E(XY - X\mu_X - Y\mu_X + \mu_X \mu_Y) \\ & = E(XY) - E(X)\mu_X - E(Y)\mu_Y + \mu_X \mu_Y \\ & = E(XY) - E(X)E(Y) \\ \end{align}$$
當X和Y獨立時,有[$E(XY) = E(X)E(Y)$],[$Cov(X,Y) = 0$]。
(注意,[$Cov(X,Y) = 0$]並不意味著X和Y獨立)
相關係數
正的協方差表達了正相關性,負的協方差表達了負相關性。對於同樣的兩個隨機變數來說,計算出的協方差越大,相關性越強。
但隨後一個問題,身高和體重的協方差為30,這究竟是多大的一個量呢?如果我們又發現,身高與鞋號的協方差為5,是否說明,相對於鞋號,身高與體重的的相關性更強呢?
這樣橫向對比超出了協方差的能力範圍。從日常生活經驗來說,體重的上下浮動大約為20kg,而鞋號的上下浮動大約可能只是5個號碼。所以,對於體重來說,5kg與中心的偏離並不算大,而5個號碼的鞋號差距,就可能是最極端的情況了。假設身高和體重的相關強度,與身高和鞋碼的相關強度類似,但由於體重本身的數值上下浮動更大,所計算出的協方差也會更大。另一個情況,依然是計算身高與體重的協方差。資料完全不變,而只更改單位。我們的體重用克而不是千克做單位,計算出的協防差是原來數值的1000倍!
為了能進行這樣的橫向對比,我們需要排除用統一的方式來定量某個隨機變數的上下浮動。這時,我們計算相關係數(correlation coefficient)。相關係數是“歸一化”的協方差。它的定義如下:
$$\rho = \frac{Cov(X, Y)}{\sqrt{Var(X)Var(Y)}}$$
相關係數是用協方差除以兩個隨機變數的標準差。相關係數的大小在-1和1之間變化。再也不會出現因為計量單位變化,而數值暴漲的情況了。
依然使用上面的身高和體重資料,可以計算出
$$Var(X) = 0.3 \times (60 - 70)^2 + 0.3 \times (80 - 70)^2= 60$$
$$Var(Y) = 0.3 \times (180 - 170)^2 + 0.3 \times (160 - 170)^2 = 60$$
$$\rho = 30 / 60 = 0.5$$
這樣一個“歸一化”了的相關係數,更容易讓人把握到相關性的強弱,也更容易在不同隨機變數之間,做相關性的橫向比較。
雙變數正態分佈
雙變數正態分佈是一種常見的聯合分佈。它描述了兩個隨機變數[$X1$]和[$X2$]的概率分佈。概率密度的表示式如下:
$$f(x_1, x_2) = \frac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1 - \rho^2}} \exp\left[ -\frac{z}{2(1 - \rho^2)} \right]$$
其中,
$$z = \frac{(x_1 - \mu_1)^2}{\sigma_1^2} - \frac{2 \rho (x_1 - \mu_1) (x_2 - \mu_2)}{\sigma_1 \sigma_2} + \frac{(x_2 - \mu_2)^2}{\sigma_2^2}$$
[$X_1$]和[$X_2$]的邊緣密度分別為兩個正態分佈,即正態分佈[$N(\mu_1, \sigma_1)$], [$N(\mu_2, \sigma_2)$]。
另一方面,除非[$\rho = 0$],否則聯合分佈也並不是兩個正態分佈的簡單相乘。可以證明,[$\rho$]正是雙變數正態分佈中,兩個變數的相關係數。
我們現在繪製該分佈的影象。可惜的是,現在的scipy.stats並沒有該分佈。我們需要自行編寫。
選取所要繪製的正態分佈,為了簡單起見,讓[$\mu_1 = 0$], [$\mu_2=0$], [$\sigma_1 = 1$],[$ \sigma_2 = 1$]。
我們先讓[$\rho = 0$],此時的聯合分佈相當於兩個正態分佈的乘積。繪製不同視角的同一分佈,結果如下。可以看到,概率分佈是中心對稱的。
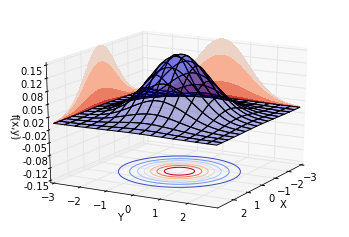
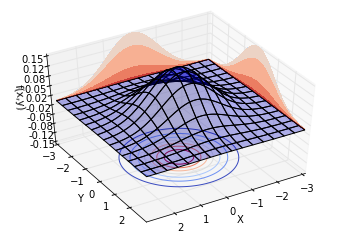
再讓[$\rho = 0.8$],也就是說,兩個隨機變數的相關係數為0.8。繪製不同視角的同一分佈,結果如下。可以看到,概率分佈並不中心對稱。沿著[$Y = X$]這條線,概率曲面隆起,概率明顯比較高。而沿著[$Y = -X$]這條線,概率較低。這也就是我們所說的正相關。
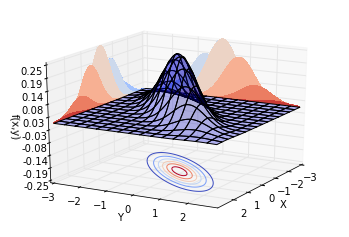
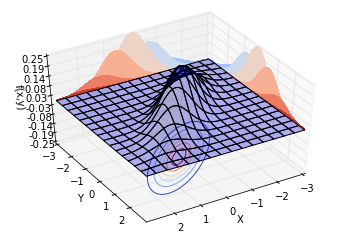
現在,[$\rho$]對於我們來說,有了更具體的現實意義。:-)
# By Vamei from scipy.stats import norm import numpy as np # this function is to generate a pdf of bivariate normal distribution def bivar_norm(mu1, mu2, sigma1, sigma2, rho): # pdf of bivariate norm def pdf(x1, x2): # get z part1 = (x1 - mu1)**2/sigma1**2 part2 = - 2.*rho*(x1 - mu1)*(x2 - mu2)/sigma1*sigma2 part3 = (x2 - mu2)**2/sigma2**2 z = part1 + part2 + part3 cof = 1./(2.*np.pi*sigma1*sigma2*np.sqrt(1 - rho**2)) return cof*np.exp(-z/(2.*(1 - rho**2))) return pdf pdf1 = bivar_norm(0, 0, 1, 1, 0) pdf2 = bivar_norm(0, 0, 1, 1, 0.8) from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm from matplotlib.ticker import LinearLocator, FormatStrFormatter import matplotlib.pyplot as plt # plot function def space_surface(pdf, xp, yp, zlim, rot1=30, rot2=30): fig = plt.figure() ax = fig.gca(projection='3d') X = np.arange(*xp) Y = np.arange(*yp) X, Y = np.meshgrid(X, Y) Z = pdf(X, Y) surf = ax.plot_surface(X, Y, Z, rstride=8, cstride=8, alpha = 0.3) cset = ax.contour(X, Y, Z, zdir='z', offset=zlim[0], cmap=cm.coolwarm) cset = ax.contourf(X, Y, Z, zdir='x', offset=xp[0], cmap=cm.coolwarm) cset = ax.contourf(X, Y, Z, zdir='y', offset=yp[0], cmap=cm.coolwarm) for angle in range(rot1 + 0, rot1 + 360): ax.view_init(rot2, angle) ax.set_zlim(*zlim) ax.zaxis.set_major_locator(LinearLocator(10)) ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f')) ax.set_xlabel("X") ax.set_ylabel("Y") ax.set_zlabel("f(x,y)") # fig.colorbar(surf, shrink=0.5, aspect=5) xp = [-3, 3, 0.05] yp = [-3, 3, 0.05] zlim1 = [-0.15, 0.15] zlim2 = [-0.25, 0.25] space_surface(pdf1, xp, yp, zlim1, 30, 20) space_surface(pdf1, xp, yp, zlim1, 60, 45) space_surface(pdf2, xp, yp, zlim2, 30, 20) space_surface(pdf2, xp, yp, zlim2, 60, 45)
總結
協方差
“歸一化”的度量: 相關係數