作者:Vamei 出處:http://www.cnblogs.com/vamei 歡迎轉載,也請保留這段宣告。謝謝!
我們瞭解了“樣本空間”,“事件”,“概率”。樣本空間中包含了一次實驗所有可能的結果,事件是樣本空間的一個子集,每個事件可以有一個發生的概率。概率是集合的一個“測度”。
這一講,我們將討論隨機變數。隨機變數(random variable)的本質是一個函式,是從樣本空間的子集到實數的對映,將事件轉換成一個數值。根據樣本空間中的元素不同(即不同的實驗結果),隨機變數的值也將隨機產生。可以說,隨機變數是“數值化”的實驗結果。在現實生活中,實驗結果可以是很“敘述性”,比如“男孩”,“女孩”。在數學家眼裡,這些文字化的敘述太過繁瑣,我們為什麼不能拿數字來代表它們呢?
(數學家恐怕是很難成為文學家吧?)

離散隨機變數
在連續擲兩次硬幣的例子中,樣本空間為:
$$\Omega = \{ HH, HT, TH, TT \}$$
這樣的實驗結果可以有很多數值化的方法,比如定義HH為400, HT為30, TH為0.2,TT為1。要注意的是,這裡是用某個數字來代表樣本空間的某個元素,這個數字並不是概率值。
如何對樣本空間的元素數值化是根據現實需求的。比如說,根據出現正面的次數,我們將贏取不同的獎勵。那麼在分析時,可以取“結果中正面的次數”為隨機變數。這樣一個隨機變數將有2, 1, 0三種可能的取值。該隨機變數只能取離散的幾個孤立值,這樣一種隨機變數稱為離散隨機變數。
對映關係如下:
| 實驗結果 | 隨機變數 |
| HH | 2 |
| HT | 1 |
| TH | 1 |
| TT | 0 |
我們通常用一個大寫字母來表示一個隨機變數,比如X。

如果樣本空間中的每個結果等概率,那麼隨機變數取值可能性為:
$$P(X=2) = 0.25$$
$$P(X=1) = 0.5$$
$$P(X=0) = 0.25$$
當X取0,1,2之外的值時,概率為0。注意到,X=1這個事件,實際上包含了兩個元素,HT, TH。因此,X=1出現的概率較高。所有可能取值的概率和為1。
[$P(X=x)$]表示了隨機變數在不同取值下的概率,稱為概率質量函式(PMF, probability mass function)。我們將看到其他的表示概率分佈的方式。
累積分佈函式
上面的函式列出了每個取值的對應概率。等價的,我們可以用累積分佈函式(CDF, cumulative distribution function)來表示隨機變數的概率分佈狀況。在累積分佈函式,我們列出的,總是隨機變數X,在小於x的這個區間的概率和。當x增大時,X < x包含的結果增加,概率和也相應增加。當x為正無窮時,實際上是所有情況的概率和,那麼累積分佈函式為1。
嚴格的定義為:
$$F(x) = P(X \le x), -\infty < x < \infty$$
我們可以繪製上面例子的CDF。
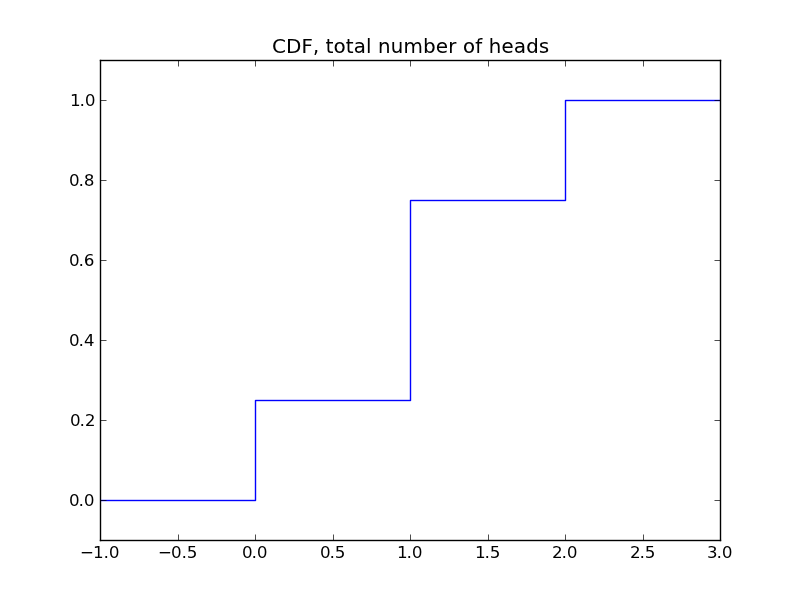
這樣的累積分佈函式似乎並不比概率質量函式來得方便。但在後面,我們會很快看到它的優勢。即它可以同時用於離散隨機變數和連續隨機變數。
上面的圖片可以用如下程式碼生成:
# By Vamei
# Plot the CDF of total number of heads in two flips
import matplotlib.pyplot as plt
x = [-1, 0, 0, 1, 1, 2, 2, 3]
y = [0, 0, 0.25, 0.25, 0.75, 0.75, 1.0, 1.0]
fig = plt.figure()
ax = plt.subplot(111)
ax.plot(x, y)
ax.set_ylim([-0.1, 1.1])
ax.set_title("CDF, total number of heads")
plt.show()
連續隨機變數
隨機變數還可以是連續取值,這樣的隨機變數稱為連續隨機變數(continuous random variable)。比如,一個隨機變數,可以隨機的取0到1的任意數值。
當這樣取值時,任意區間能實際上都有無窮多個結果。比如,我們測量溫度,可以有1度和2度,但兩者之間,還可以有1.1度,1.003度,1.658度等等無窮種結果。這樣的話,每個結果的可能性都是無窮小。我們討論的是某個區間內的概率,即[$P(a<X<b)$],而不是具體某一數值的概率。在這樣的情況下,分到各個結果的概率都無限趨近於0。顯然,我們無法用概率質量函式來描述連續隨機變數的分佈。
我們這裡遇到的困境是現代數學的一個相當的困擾。考慮一個線段,它是點的集合,並且有“長度”這樣的測度。然而,線段上有無窮個多個點。討論“每個點的長度”是完全沒有意義的。將線段換成區間,將點換成取值,將長度換成概率,我們發現這兩個問題異常相似。另一方面,我們知道,可以從線段上擷取某一小段,而這一小段是可以有“長度”的。連續隨機變數的概率定義,正依賴於此:對於連續隨機變數,我們只討論某個區間,比如從1.2到1.4這一區間的概率,而不討論具體某個點,比如1.3的概率。

觀察一個很簡單的連續隨機分佈。假設我們有一個隨機數生成器,產生一個從0到1的實數,每個實數出現的概率相等。這樣的一個分佈被稱為均勻分佈(uniform distribution)。直覺告訴我們,相同長度的每一段區間,對應的概率都相同。由此,[0, 0.5]是整個區間的一半,概率為1/2。對於均勻分佈來說,概率正好和區間長度這一測度等同。
我們嘗試用更正式的方式來描述分佈。累積分佈函式本身就表示隨機變數在一個區間概率,所以可以直接用於連續隨機變數。即
$$F(x) = P(X \le x), - \infty < x < \infty$$
對於均勻分佈來說,它的累積分佈函式是:
$$F(x) = 0, x < 0$$
$$F(x) = x, 0 \le x \le 1 $$
$$F(x) = 1, x > 1$$
它類似從線段的一頭到某一點的“長度”。這樣,我們就知道了從起點到每一點的長度。如果我們想知道某個特定區間[a, b]的概率,它就是F(b) - F(a)。
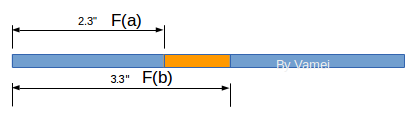
借用“無窮小”的概念,我們可以構建概率密度函式(PDF,probability density function)。粗糙的講,我們在某個點附近取一個“無窮小”段,該小段的區間長度為dx,而這個“無窮小”段對應的概率為dF,那麼該點的概率密度為dF/dx。這實際上是微積分的領域。
概率密度函式可以代替累積分佈函式,來表示一個連續隨機變數的概率分佈:
$$f(x) = \frac{dF(x)}{dx}$$
即密度函式是累積分佈函式的微分,或者說,
$$F(x) = \int_{-\infty}^x f(u)du$$
即累積分佈函式是密度函式從負無窮到x的積分。
密度函式滿足:
$$\int_{-\infty}^{+\infty} f(u)du = 1$$
均勻分佈的密度函式可以寫成:
$$f(x) = \left\{ \begin{array}{l} 1, 0 \leq x \leq 1 \\ 0, x<0 \, or \, x>1 \end{array}\right.$$
可以畫出該密度函式
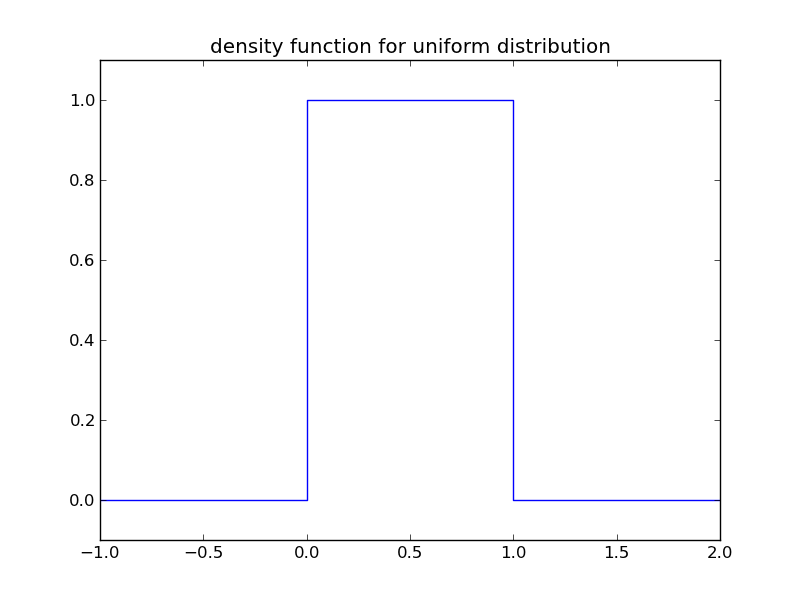
對一個函式的積分,獲得的是該函式曲線下的面積。因此,密度曲線下某個區間的面積,就是密度概率函式的積分,代表了隨機變數在該區間的概率。概率密度函式就可以非常直觀的通過“面積”,來表示概率的大小。
從負無窮到正無窮積分,就代表了所有可能結果的概率和,即為1。
上面的圖片可以利用下面程式碼生成:
# By Vamei # Density function for uniform distribution import matplotlib.pyplot as plt x = [-1, 0, 0, 1, 1, 2] y = [0, 0, 1, 1, 0, 0] fig = plt.figure() ax = plt.subplot(111) ax.plot(x, y) ax.set_xlim([-1, 2]) ax.set_ylim([-0.1, 1.1]) ax.set_title("density function for uniform distribution") plt.show()
總結
隨機變數,隨機變數的概率分佈
累積分佈函式
密度函式
歡迎繼續閱讀“資料科學”系列文章