Leetcode Unique Paths

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

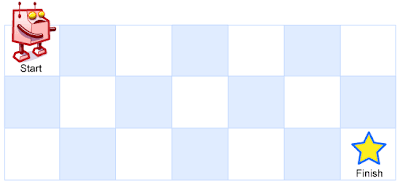
Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

設mxn的表格，前面增加一列為mX(n+1), 注意對於

第i行第j列的元素path[i][j]，其路徑前一個點只有path[i-1][j]和path[i][j-1]兩種可能

即path[i][j] =path[i-1][j] + path[i][j-1]，而path[i-1][j]為上面一行的元素，而path[i][j-1]為其左邊的元素

當更新path[i][j]時，此時左邊元素已經更新，只需要用滾動陣列實現即可

path[0]	path[1]	path[2]	path[3]	path[4]	path[5]	path[6]	path[7]
path[0]	path[1]	path[2]=path[1]+path[2]
path[0]

 

 

 

 

 

 

int unique(int m, int n){
    vector<int> path(n+1,1);
    path[0] = 0;
    for(int i = 0 ; i < m; ++ i){
        for(int j = 1; j<= n ; ++ j){
            path[j]+=path[j-1];
        }
    }
    return path[n];
}