前言
對於如何發現一個資料集中的頻繁項集,前文講解的經典 Apriori 演算法能夠做到。
然而,對於每個潛在的頻繁項,它都要檢索一遍資料集,這是比較低效的。在實際的大資料應用中,這麼做就更不好了。
本文將介紹一種專門檢索頻繁項集的新演算法 - FP-growth 演算法。它只會掃描資料集兩次,能順序挖掘出頻繁項集。因此這種演算法在網頁資訊處理中佔據著非常重要的地位。
FP-growth 演算法基本原理
將資料儲存到一種成為 FP 樹的資料結構中,這樣的一棵樹包含了資料集中滿足最小支援度閾值的所有節點資訊以及對應的支援度資訊。
構建好了 FP 樹之後,通過一定規則遍歷這棵樹就能挖掘出頻繁項集。
PS:後面會專門講解如何實現這樣的一棵樹,以及如何遍歷這棵樹。
FP 樹
下圖為 FP 樹架構示意圖:
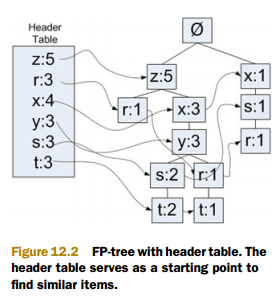
1. 右邊部分中,"z:5" 的意思是,z在這條路徑上出現了5次(包含其單個出現,也包含組合出現的情況);
2. 順著 "z:5" 往下,看到的是 r=1。這表示在這條路徑上 "zr" 出現了一次;
3. 每個節點在樹中都不是唯一的,比如能夠清楚看到 r 出現了好幾次;
4. 左邊的部分,存放的是所有原子項出現的個數(包含其單個出現,也包含組合出現的情況),同時它還 ”派生" 出一個連結串列將所有樹結構部分中的相同原子項串起來;
5. 比如左邊部分 r=3 就派生出一個連結串列串起了 3 個 r 節點,每個 r 節點標記都為1,故左邊部分 r=3。
構建 FP 樹
FP 樹的機構稍微有點複雜,因此就不用字典,轉用類(物件)來存樹了。
下面是 FP 樹結構的程式碼實現:
1 class treeNode: 2 'FP 樹節點' 3 4 #===================================== 5 # 輸入: 6 # nameValue: 節點名稱 7 # numOccur: 節點路徑出現次數 8 # parentNode: 父節點 9 #===================================== 10 def __init__(self, nameValue, numOccur, parentNode): 11 '初始化函式' 12 13 # 節點名字 14 self.name = nameValue 15 # 節點的路徑出現次數 16 self.count = numOccur 17 # 指向相似節點 18 self.nodeLink = None 19 # 父節點 20 self.parent = parentNode 21 # 子節點 22 self.children = {} 23 24 #===================================== 25 # 輸入: 26 # numOccur: 節點路徑出現次數增量 27 #===================================== 28 def inc(self, numOccur): 29 '增加節點出現次數' 30 31 # 增加這個節點的路徑出現次數 32 self.count += numOccur 33 34 #===================================== 35 # 輸入: 36 # ind: 節點路徑出現次數增量 37 # ind: 子樹序號 38 #===================================== 39 def disp(self, ind=1): 40 '將樹以文字形式顯示' 41 42 print ' '*ind, self.name, ' ', self.count 43 for child in self.children.values(): 44 child.disp(ind+1)
以上程式碼定義的基本的 FP 樹節點資料結構。接下來就是樹生成部分以及表頭(見上一部分圖中左部)生成部分程式碼:
1 def loadSimpDat(): 2 '載入測試資料' 3 4 simpDat = [['r', 'z', 'h', 'j', 'p'], 5 ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'], 6 ['z'], 7 ['r', 'x', 'n', 'o', 's'], 8 ['y', 'r', 'x', 'z', 'q', 't', 'p'], 9 ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']] 10 return simpDat 11 12 def createInitSet(dataSet): 13 '將測試資料格式化為字典' 14 15 retDict = {} 16 for trans in dataSet: 17 retDict[frozenset(trans)] = 0 18 for trans in dataSet: 19 retDict[frozenset(trans)] += 1 20 return retDict 21 22 #===================================== 23 # 輸入: 24 # dataSet: 資料集 25 # minSup: 最小支援度(實際為次數) 26 # 輸出: 27 # retTree: FP 樹結構 28 # headerTable: 表結構 29 #===================================== 30 def createTree(dataSet, minSup=1): 31 '建立 FP 樹及其對應表結構' 32 33 # 連續兩次遍歷資料集。第一次獲取所有資料項及個數;第二次會支援度過濾。 34 # 單元素頻繁集(含出現次數) 35 headerTable = {} 36 for trans in dataSet: 37 for item in trans: 38 headerTable[item] = headerTable.get(item, 0) + dataSet[trans] 39 for k in headerTable.keys(): 40 if headerTable[k] < minSup: 41 del(headerTable[k]) 42 43 # 單元素頻繁集(不含次數) 44 freqItemSet = set(headerTable.keys()) 45 # 沒有合乎要求的資料項則退出 46 if len(freqItemSet) == 0: 47 return None, None 48 49 # 對錶資料結構進行格式化,使之能夠存放指標。 50 for k in headerTable: 51 headerTable[k] = [headerTable[k], None] 52 53 # 新建初始化樹節點 54 retTree = treeNode('Null Set', 1, None) 55 for tranSet, count in dataSet.items(): 56 57 # 當前事務的單元素集(含次數) 58 localD = {} 59 for item in tranSet: 60 if item in freqItemSet: 61 localD[item] = headerTable[item][0] 62 63 if len(localD) > 0: 64 # 對localD中所有元素進行排序 65 orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)] 66 # 更新 FP 樹 67 updateTree(orderedItems, retTree, headerTable, count) 68 69 # 返回FP樹和表頭結構 70 return retTree, headerTable 71 72 #===================================== 73 # 輸入: 74 # items: 事務項 75 # inTree: FP 樹 76 # headerTable: 表結構 77 # count: 事務項的個數 78 #===================================== 79 def updateTree(items, inTree, headerTable, count): 80 'FP 樹生長函式' 81 82 # 檢查事務項中的第一個元素是否作為樹的直接子節點存在 83 if items[0] in inTree.children: 84 # 存在則直接更新子樹節點 85 inTree.children[items[0]].inc(count) 86 else: 87 # 不存在則更新樹結構 88 inTree.children[items[0]] = treeNode(items[0], count, inTree) 89 # 更新表結構 90 if headerTable[items[0]][1] == None: 91 headerTable[items[0]][1] = inTree.children[items[0]] 92 else: 93 updateHeader(headerTable[items[0]][1], inTree.children[items[0]]) 94 95 # 遞迴呼叫此樹生長函式 96 if len(items) > 1: 97 updateTree(items[1::], inTree.children[items[0]], headerTable, count) 98 99 #===================================== 100 # 輸入: 101 # nodeToTest: 指定表結構中的成員 102 # targetNode: 待加入連結串列節點的指標 103 #===================================== 104 def updateHeader(nodeToTest, targetNode): 105 '表結構更新函式' 106 107 while (nodeToTest.nodeLink != None): 108 nodeToTest = nodeToTest.nodeLink 109 110 nodeToTest.nodeLink = targetNode 111 112 def main(): 113 'FP 樹構建與展示' 114 115 # 載入測試資料 116 simpDat = loadSimpDat() 117 # 將測試資料格式化為字典 118 initSet = createInitSet(simpDat) 119 # 建立 FP 樹及對應表結構 120 myFPTree, myHeaderTab = createTree(initSet, 3) 121 # 展示 FP 樹 122 myFPTree.disp()
測試結果:
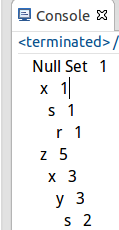
從 FP 樹中挖掘頻繁項集
FP 樹構建好之後,就能對它進行挖掘,以找到所有頻繁項集。
挖掘過程僅僅針對 FP 樹和它對應的表結構,與原資料集沒有任何關係了。
具體挖掘步驟如下:
1. 從 FP 樹中獲得條件模式基;
2. 利用條件模式基,獲得一個條件 FP 樹;
3. 迭代 1,2 直到樹只剩下一個元素項。
下面分別講解如何抽取條件模式基,以及如何從條件模式基構建 FP 樹。
條件模式基的抽取
條件模式是指以所查詢元素項為結尾的路徑。
對於如下 FP 樹來說:

r 的條件模式基為 {z},{x,s},{z,x,y} 。
而上圖的左部表結構就是用來求取抽象基的一個輔助結構。通過每個子連結串列的每個節點都能向上迭代獲取到一個路徑,一個連結串列得到的所有路徑和就是該連結串列元素項對應的條件模式基。
如下部分程式碼可用來求取元素項的條件模式基:
1 #===================================== 2 # 輸入: 3 # leafNode: 表結構的子連結串列的節點 4 # prefixPath: 待返回路徑 5 #===================================== 6 def ascendTree(leafNode, prefixPath): 7 '獲取FP樹某個葉子節點的字首路徑' 8 9 if leafNode.parent != None: 10 prefixPath.append(leafNode.name) 11 ascendTree(leafNode.parent, prefixPath) 12 13 #===================================== 14 # 輸入: 15 # basePat: 元素項 16 # treeNode: 某個連結串列指向某首葉子節點的指標 17 #===================================== 18 def findPrefixPath(basePat, treeNode): 19 '獲取表結構中某個元素項的條件模式基' 20 21 # 條件模式基 22 condPats = {} 23 24 # 獲取某個元素項的條件模式基礎並返回 25 while treeNode != None: 26 prefixPath = [] 27 ascendTree(treeNode, prefixPath) 28 if len(prefixPath) > 1: 29 condPats[frozenset(prefixPath[1:])] = treeNode.count 30 treeNode = treeNode.nodeLink 31 32 return condPats
條件 FP 樹的構建與頻繁項集的挖掘
對於每個頻繁項,都要建立一個條件 FP 樹。
條件 FP 樹的建立程式碼,和之前的 FP 樹是一樣的。不過輸入資料集會變成第一次求出的條件模式。
而且,第一次挖掘的僅僅是最小元素項,而後面挖掘出的頻繁項都會基於上一步結果疊加。如此一直迭代下去直到表結構為空。
實現程式碼如下:
1 #===================================== 2 # 輸入: 3 # inTree: 條件FP樹 4 # headerTable: 條件表頭結構 5 # minSup: 最小支援度 6 # preFix: 上一輪的頻繁項 7 # freqItemList: 頻繁項集 8 #===================================== 9 def mineTree(inTree, headerTable, minSup, preFix, freqItemList): 10 '挖掘頻繁項集' 11 12 # 對錶結構進行重排序(由小到大) 13 bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: p[1])] 14 15 # 遍歷表結構 16 for basePat in bigL: 17 # 生成新頻繁子項 18 newFreqSet = preFix.copy() 19 newFreqSet.add(basePat) 20 # 加入頻繁集 21 freqItemList.append(newFreqSet) 22 # 挖掘新的條件模式基 23 condPattBases = findPrefixPath(basePat, headerTable[basePat][1]) 24 # 建立新的條件FP樹 25 myCondTree, myHead = createTree(condPattBases, minSup) 26 # 若表結構非空,遞迴挖掘。 27 if myHead != None: 28 mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)
測試結果:

小結
1. FP-growth 演算法使用了新的資料結構,而且建立,遍歷過程遞迴程式碼比較多,因此理解起來有點難度。
2. FP-growth 演算法一般用來用來挖掘頻繁項集,不用來學習關聯規則。
3. 大資料領域中機器學習的部分就暫告一段落了(已學習完最為經典的演算法)。接下來的精力將主要放在 Hadoop 雲平臺的使用及其底層機制實現部分。