第十篇：非均衡分類問題的思考與問題與解決思路

穆晨發表於2017-01-19

前言

       在前面的文章中，討論了一些分類演算法。然後，有一點一直忽視了，就是非均衡的分類問題。

       分均衡分類有兩種情形

              情形一：正例和反例數量相差非常大。

              比如，分析信用卡資訊集裡面的正常樣本和詐騙樣本。正常樣本固然比詐騙樣本要多的多了。

              情形二：分類正確/錯誤的代價不同。

              比如，分析病人的體檢資料，我們肯定是希望不漏過任何一個病例。因此，有病診斷為無病的後果要比無病診斷為有病的後果嚴重的多。

       這樣的非均衡分類的情形導致了僅僅是使用分類錯誤率還分析分類質量是不科學的。

       本文就將介紹一些新的衡量分類質量的引數，工具。基於這些，可以對分類程式碼進行優化，以得到更符合實際用途的分類器。

工具一：混淆矩陣 (confusion matrix)

       首先介紹幾個概念：

       1. TP: 真陽。就是實際為真 預測為真。

       2. FN: 假陽。就是實際為真 預測為假。

       3. FP: 假陰。就是實際為假 預測為真。

       4. TN: 真陰。就是實際為假 預測為假。

       列出這幾個引數的詳細表格(矩陣格式)即為混淆矩陣，如下圖所示：

      

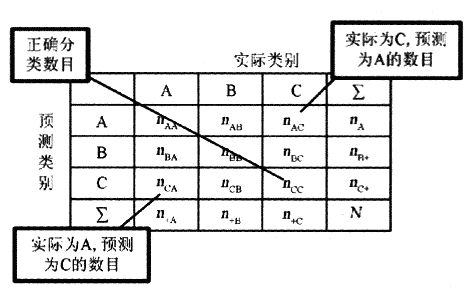
       這樣的表格能夠很好的幫助人們進行分類的質量評估。然而，對於程式，或者說機器來說，需要的是一個基於代價的硬性指標。

       因此，下面這個工具 - ROC曲線才是機器學習中處理非均衡分類問題的利器。

工具二：ROC 曲線

       ROC 曲線圖就是一個平面的二維圖。橫軸為假陽率；縱軸為真陽率。

       真陽率 = TP / (TP+FN)。就是實際為真，預測也為真的樣本在所有實際為真的樣本中的概率。

       假陽率 = FP / (FP+TN)。就是實際為假，預測為真的樣本在所有實際為假的樣本中的概率。

       而移動的方向是按照閾值變化而變化的。每個點代表了一個閾值的真陽率和假陽率。

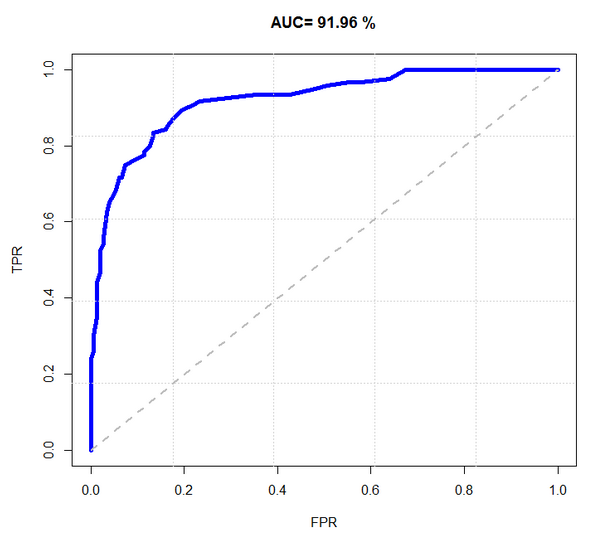
       如下圖所示例：

       m

       對於 ROC 模型，圖中藍色線段與橫軸的面積佔總面積的比率 - AUC 可以衡量整個分類的效能，但是切記它不能代替對整個線段以及錯誤率的觀察。

       AUC理論最佳值是1。如果說 "真” 這一類的權重更重要(好比診斷出病人有病)，那麼AUC應該在0.5 - 1之間才好，而且是越接近1越好。

繪製 ROC 曲線

       繪製 ROC 曲線首先必須要獲取到分類器結果的預測強度，基於預測強度才能夠調整真陽率，假陽率。

       如下程式碼是 ROC 統計圖的繪製程式碼，可將其進行封裝，以在需要時隨時呼叫。

 1 #==========================================
 2 # 輸入:
 3 #        predStrengths:    預測強度
 4 #        classLabels:    分類結果
 5 # 輸出:
 6 #        該分類器的ROC統計圖
 7 #==========================================
 8 def plotROC(predStrengths, classLabels):
 9     '繪製分類器的ROC統計圖'
10     
11     import matplotlib.pyplot as plt
12     # 當前繪製節點
13     cur = (1.0,1.0)
14     # AUC 統計
15     ySum = 0.0 
16     # 實際為真的分類數
17     numPosClas = sum(numpy.array(classLabels)==1.0)
18     # x軸移動步長
19     yStep = 1/float(numPosClas); 
20     # y軸移動步長
21     xStep = 1/float(len(classLabels)-numPosClas)
22     # 預測強度排序(下標排序)
23     sortedIndicies = predStrengths.argsort()
24     # 設定畫布
25     fig = plt.figure()
26     fig.clf()
27     ax = plt.subplot(111)
28     
29     # 以預測強度遞減的次序繪製ROC統計影象
30     for index in sortedIndicies.tolist()[0]:
31         if classLabels[index] == 1.0:
32             delX = 0; delY = yStep;
33         else:
34             delX = xStep; delY = 0;
35             ySum += cur[1]
36         
37         ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY], c='b')
38         cur = (cur[0]-delX,cur[1]-delY)
39         
40     ax.plot([0,1],[0,1],'b--')
41     plt.xlabel('False positive rate'); plt.ylabel('True positive rate')
42     plt.title('ROC curve for AdaBoost horse colic detection system')
43     ax.axis([0,1,0,1])
44     plt.show()
45     print "the Area Under the Curve is: ",ySum*xStep

       採用上函式對上一篇文章中的 AdaBoost 分類器(10次迭代)繪製 ROC 統計直方圖的結果如下(資料集格式和以前一樣，內容都是隨機生成的。)：

　　

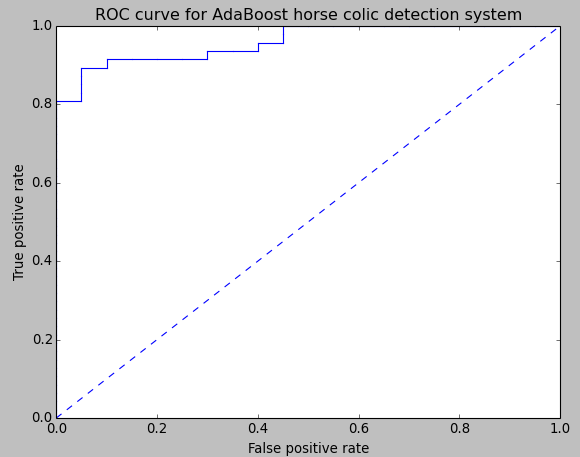
其他一些度量方案

       1. 可設立代價函式，計算混淆矩陣的代價值(所有成員乘以對應權重然後求和)。

       2. 對於那種樣本數量不均衡的問題(如信用卡詐騙這類)，可以調整樣本數量。比如5000和真樣本，50個假樣本，那麼就從這5000個真樣本里只隨機選擇50個真樣本。

小結

       關於分類演算法的討論，先告一段落了。

       以後可能會有對其中某些演算法的進一步分析的學習文章分享，但現在我的目光將從分類轉移到監督學習中的下一個主題 - 迴歸。

       元旦第二天假期也快結束了，新的一年要加把勁，好好學習的同時多多注意鍛鍊身體，迎接充滿挑戰的未來。

相關文章