前言
有人認為 AdaBoost 是最好的監督學習的方式。
某種程度上因為它是元演算法,也就是說它會是幾種分類器的組合。這就好比對於一個問題能夠諮詢多個 "專家" 的意見了。
組合的方式有多種,可能是不同分類演算法的分類器,可能是同一演算法在不同設定下的整合,還可以是資料集在不同部分分配給不同分類器之後的整合等等。
本文將給出的 AdaBoost 分類器實現基於第二種 (另外幾種實現在此基礎上稍作改動即可)。
一種原始的元演算法 - bagging (自舉匯聚法)
這個演算法的意思有點像投票系統,其思路步驟大致如下:
1. 將資料按照一定的規則劃分成 N 份,每份的大小和原資料集一樣大 (因此裡面肯定是有重複資料的)。
2. 將這 N 份資料集分發到多個分類器中。
3. 按照 "少數服從多數" 原則,從這 N 個分類器的分類結果中總結出最優結果。
boost (提高任意給定學習演算法精確度演算法) vs bagging (自舉匯聚法)
boost 和 bagging 一個很大的不同是它會給那些分錯的樣本更高關注度(權重)。AdaBoost 是一種最為典型的 boost 元演算法。
因此理論上它能在相對較少的迭代次數下得到更為精確的分類結果。
AdaBoost 元演算法的基本原理
AdaBoost 的強大之處,在於它能夠整合多個弱分類器,形成一個強分類器。
所謂弱分類器就是分類錯誤率大於五成的分類器,比隨機分類還渣。(但是它的分類演算法是確定的,這點和隨機分類器不同。顯然你無法通過整合隨機分類器得到什麼有價值的東西)
其具體步驟大致如下:
1. 對每個樣本給定一個權重 d。
2. 基於權重向量 D 呼叫一次弱分類器並得出這次統計的分類器權重值 alpha (注意是分類器權重值,區別於上一步的權重d)
3. 基於分類器權重值 alpha 更新各個樣本的權重向量
4. 迴圈 2 - 3 直到錯誤率為 0 或者迴圈到了指定的次數
5. 1-4 為訓練部分演算法,訓練好了之後,便可帶入樣本進行分類。分類的方法是依次帶入訓練集中的各個分類器中求出分類結果,然後各部分結果乘以其對應的分類器權重值 alpha 再累加求和。
下圖可用來幫助理解 (直方圖中的矩形長度表示樣本權重,三角形中的值表示分類器權重值 alpha):
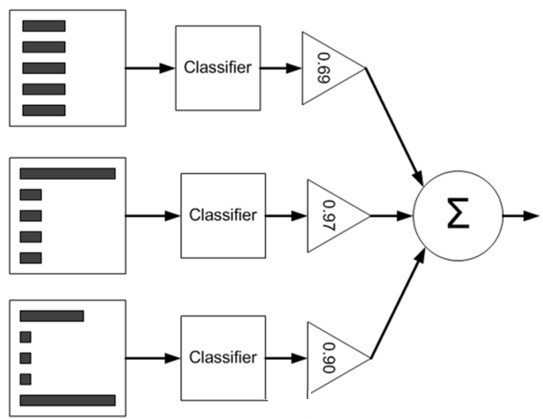
基於單層決策樹的 AdaBoost 元演算法分類器實現
首先,準備好單層決策樹的資料結構。
在本文的 AdaBoost 實現中,元演算法中的分類器組合模式是 "同一演算法在不同設定下的整合",那麼不同設定不同在哪裡?
不同就不同在每次構建單層決策樹都是選擇劃分正確率最高的劃分方式。
因此在構建單層決策樹函式中,必須有一個擇優過程,具體可以參考下面的實現程式碼。
函式的功能應當是返回一個單層決策樹資訊結構(僅僅是劃分資訊就可以了不用資料)。
同時,函式應該返回一個錯誤資訊值,這個錯誤值是和權重向量D相關的,用於計算分類器權重值 alpha。(當然也可以在該函式內部實現該欄位)
最後,分類結果自然也要返回。
單層決策樹程式碼實現如下:
1 #========================================== 2 # 輸入: 3 # dataMatrix: 輸入資料 4 # dimen: 劃分特徵下標 5 # threshVal: 劃分閾值 6 # threshIneq: 劃分方向(是左1右0分類還是左0右1分類) 7 # 輸出: 8 # retArray: 分類結果 9 #========================================== 10 def stumpClassify(dataMatrix,dimen,threshVal,threshIneq): 11 '按照指定方式分類並返回結果' 12 13 retArray = numpy.ones((numpy.shape(dataMatrix)[0],1)) 14 if threshIneq == 'lt': 15 retArray[dataMatrix[:,dimen] <= threshVal] = -1.0 16 else: 17 retArray[dataMatrix[:,dimen] > threshVal] = -1.0 18 19 return retArray 20 21 22 #========================================== 23 # 輸入: 24 # dataArr: 輸入資料 25 # classLabels: 分類標籤集 26 # D: 權重向量 27 # 輸出: 28 # bestStump: 決策樹資訊 29 # minError: 帶權錯誤(用於生成分類器權重值 alpha) 30 # bestClasEst: 分類結果 31 #========================================== 32 def buildStump(dataArr,classLabels,D): 33 '建立單層最佳決策樹' 34 35 dataMatrix = numpy.mat(dataArr); 36 labelMat = numpy.mat(classLabels).T 37 m,n = numpy.shape(dataMatrix) 38 39 # 特徵值閾值步長 40 numSteps = 10.0; 41 # 當前最佳決策樹資訊集 42 bestStump = {}; 43 # 分類結果 44 bestClasEst = numpy.mat(numpy.zeros((m,1))) 45 # 最小帶權錯誤初始化為無窮大 46 minError = numpy.inf 47 48 for i in range(n): # 遍歷所有的特徵選取最佳劃分特徵 49 rangeMin = dataMatrix[:,i].min(); 50 rangeMax = dataMatrix[:,i].max(); 51 stepSize = (rangeMax-rangeMin)/numSteps 52 53 for j in range(-1,int(numSteps)+1): # 遍歷所有的特徵值選取最佳劃分特徵值 stepSize為探測步長 54 55 for inequal in ['lt', 'gt']: # 對於 左1右0 和 左0右1 兩種分類方式 56 57 # 當前劃分閾值 58 threshVal = (rangeMin + float(j) * stepSize) 59 # 分類 60 predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal) 61 # 統計分類錯誤資訊 62 errArr = numpy.mat(numpy.ones((m,1))) 63 errArr[predictedVals == labelMat] = 0 64 weightedError = D.T*errArr 65 66 # 更新最佳決策樹的資訊 67 if weightedError < minError: 68 minError = weightedError 69 bestClasEst = predictedVals.copy() 70 bestStump['dim'] = i 71 bestStump['thresh'] = threshVal 72 bestStump['ineq'] = inequal 73 74 return bestStump,minError,bestClasEst
在單層決策樹之上,便是 AdaBoost 分類器的實現,下面先給出虛擬碼:
1 對每次迭代: 2 找到最佳單層決策樹 3 將該樹加入到最佳決策樹陣列 4 計算分類器權重 alpha 5 更新權重向量 D 6 更新累計類別估計值 7 PS: 如果錯誤率等於0.0,則立馬退出迴圈。
Python 程式碼實現如下:
1 #========================================== 2 # 輸入: 3 # dataArr: 輸入資料 4 # classLabels: 分類標籤集 5 # numIt: 最大迭代次數 6 # 輸出: 7 # bestStump: 決策樹資訊 8 # minError: 帶權錯誤(用於生成分類器權重值 alpha) 9 # bestClasEst: 分類結果 10 #========================================== 11 def adaBoostTrainDS(dataArr,classLabels,numIt=40): 12 'AdaBoost 分類器' 13 14 # 最佳決策樹集合 15 weakClassArr = [] 16 # 樣本個數 17 m = numpy.shape(dataArr)[0] 18 # 權重向量 19 D = numpy.mat(numpy.ones((m,1))/m) 20 # 各個類別的估計累積值 21 aggClassEst = numpy.mat(numpy.zeros((m,1))) 22 23 for i in range(numIt): # 迭代 numIt 次 24 # 構建最佳決策樹 25 bestStump,error,classEst = buildStump(dataArr,classLabels,D) 26 # 計算該決策樹的分類器權重值 alpha 27 alpha = float(0.5*numpy.log((1.0-error)/max(error,1e-16))) 28 bestStump['alpha'] = alpha 29 # 將該決策樹加入到決策樹陣列中去 30 weakClassArr.append(bestStump) 31 32 # 更新權重向量 33 expon = numpy.multiply(-1*alpha*numpy.mat(classLabels).T,classEst) 34 D = numpy.multiply(D,numpy.exp(expon)) 35 D = D/D.sum() 36 37 # 計算當前的總錯誤率。如果錯誤率為0則退出迴圈。 38 aggClassEst += alpha*classEst 39 aggErrors = numpy.multiply(numpy.sign(aggClassEst) != numpy.mat(classLabels).T,numpy.ones((m,1))) 40 errorRate = aggErrors.sum()/m 41 print "錯誤率: ",errorRate 42 if errorRate == 0.0: break 43 44 return weakClassArr
至此,就可以用 AdaBoost 進行分類了。
首先訓練出一個訓練集,然後將訓練集帶入分類函式,如下:
1 # 獲取訓練集 2 classifierArr = adaBoostTrainDS(daaArr, labelArr, 30) 3 # 分類並列印結果 4 print adaClassify([0,0], classifierArr)
測試結果:

顯然,可以看出 AdaBoost 分類器由三個決策樹構成。樣本最終分類結果為 -1。
小結
本文介紹了分類器中的元演算法思想。通過這樣的思想,能夠將多種分類器組合起來,大大地加強了分類效能。
另外據可靠資料分析,較之邏輯迴歸,AdaBoost 分類器沒有過度擬合(overfitting)現象。
Boost演算法還有很多種,AdaBoost 只是其中最為經典的實現之一,還有更多高階實習需要在日後學習工作中進行研究。