1. SIFT演算法中一些符號的說明
$I(x,y)$表示原影象。
$G(x,y,\sigma)$表示高斯濾波器,其中$G(x,y,\sigma) = \frac{1}{2\pi\sigma^2}exp(-(x^2+y^2)/2\sigma^2)$。
$L(x,y,\sigma)$表示由一個高斯濾波器與原影象卷積而生成的影象,即$L(x,y,\sigma) = G(x,y,\sigma)\otimes I(x,y)$。一系列的$\sigma_i$,則可以生成一系列的$L(x,y,\sigma_i)$影象,此時我們把這一系列的$L(x,y,\sigma)$影象稱為原影象的一個尺度空間表示。關於尺度空間的知識可以參考:影象特徵提取:尺度空間理論。
$DOG$表示高斯差分(Difference of Gaussians),也可以表示為$D(x,y,\sigma)$,其中$D(x,y,\sigma) = (G(x,y,k\sigma) – G(x,y,\sigma))\otimes I(x,y) = L(x,y,k\sigma) – L(x,y,\sigma)$。
上面特別值得注意的是尺度為$\sigma$的高斯差分影象由於尺度為$k\sigma$與尺度為$\sigma$的L影象生成的。$k$為兩相鄰尺度空間倍數的常數。
$O$:高斯金字塔的組數(Octave),其中值得注意的是在實際構建中,第一組的索引可以為0也可以為-1,這個在後面解釋原理。
$S$:高斯金字塔每一組的層數。在實際最開始構建尺度空間影象,即L影象的時候,構建了S+3層,一定要把這個S+3與S區分開,為什麼是S+3後面分析。
2. 構建高斯差分金字塔
2.1 第一組第一層影象的生成
很多初涉SIFT的都會被這個問題所困惑,這裡要分兩種情況:其一是把第一組的索引定為0;其二是把第一組的索引定為-1。
我們先考慮第一組索引為0的情況,我們知道第一組第一層的影象是由原影象與$\sigma_o$(一般設定為1.6)的高斯濾波器卷積生成,那麼原影象是誰呢?是$I(x,y)$嗎?不是!為了影象反走樣的需要,通常假設輸入影象是經過高斯平滑處理的,其值為$\sigma_n = 0.5$,即半個像元。意思就是說我們採集到的影象$I(x,y)$,已經被$\sigma = \sigma_n = 0.5$的高斯濾波器平滑過了。所以我們不能直接對$I(x,y)$用$\sigma_0$的高斯濾波器平滑,而應該用$\sigma = \sqrt{\sigma_0^2 - \sigma_n^2}$的高斯濾波器去平滑$I(x,y)$,即
$$FirstLayer(x,y) = I(x,y)\otimes G(x,y,\sqrt{\sigma_0^2 - \sigma_n^2})$$
其中$FirstLayer(x,y)$表示整個尺度空間為第1組第1層的影象,$\sigma_o$一般取1.6,$\sigma_n = 0.5$。
現在我們來考慮把第一組的索引定為-1的情況。那麼首先第一個問題便是為什麼要把索引定為-1。如果索引為0,如上面那種情況所示,整個尺度空間的第1組的第1層影象已經是由原影象模糊生成的了,那麼也就是說已經丟失了細節資訊,那麼原影象我們完全沒有利用上。基於這種考慮,我們先將影象放大2倍,這樣原影象的細節就隱藏在了其中。由上面一種情況分析,我們已經知識了I(x,y)看成是已經被$\sigma_n = 0.5$模糊過的影象,那麼將$I(x,y)$放大2倍後得到$I_s(x,y)$,則可以看為是被$2\sigma_n= 1$的高斯核模糊過的影象。那麼由$I_s$生成第1組第1層的影象用的高斯濾波器的$\sigma = \sqrt{\sigma_0^2 -(2 \sigma_n)^2}$。可以表示為。
$$FirstLayer(x,y) = I_s(x,y)\otimes G(x,y,\sqrt{\sigma_0^2 - (2\sigma_n)^2})$$
其中$FirstLayer(x,y)$表示整個尺度空間為第1組第1層的影象,$I_s(x,y)$是由$I(x,y)$用雙線性插值放大後的影象。$\sigma_o$一般取1.6,$\sigma_n = 0.5$。
2.2 尺度空間生成了多少幅影象
我們知道S是我們最終構建出來的用來尋找特徵點的高斯差分影象,而特徵點的尋找需要查詢的是空間區域性極小值,即在某一層上查詢區域性極值點的時候需要用到上一層與下一層的高斯差分影象,所以如果我們需要查詢S層的特徵點,需要S+2層高斯差分影象,然後查詢其中的第2層到第S+1層。
而每一個高斯差分影象$G(x,y,\sigma)$都需要兩幅尺度空間的影象$L(x,y,k\sigma)$與$L(x,y,\sigma)$進行差分生成,這裡假設S =3,則我們需要的高斯差分影象有S+2 = 5張,分別為$G(x,y,\sigma),G(x,y,k\sigma),G(x,y,k^2\sigma),G(x,y,k^3\sigma),G(x,y,k^4\sigma)$。其中的$G(x,y,k\sigma),G(x,y,k^2\sigma),G(x,y,k^3\sigma)$這三張影象是我們用來查詢區域性極值點的影象。那麼我們則需要S+3 = 6張尺度空間影象來生成上面那些高斯差分影象,它們分別為:$L(x,y,\sigma),L(x,y,k\sigma),L(x,y,k^2\sigma),L(x,y,k^3\sigma),L(x,y,k^4\sigma),L(x,y,k^5\sigma)$
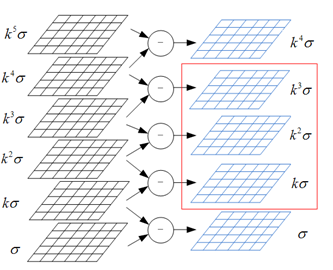
從上面的分析,我們知道對於尺度空間來說,我們一共需要S+3層影象來構建出來S+2層高斯差分影象。所以,如果整個尺度空間一共有O組,每組有S+3層影象。共O*(S+3)張尺度影象,如果我們查詢OpenCV中的SIFT原始碼,則很容易找到如下程式碼來說明問題:
pyr.resize(nOctaves*(nOctaveLayers + 3));
上面程式碼中的pyr代表了整個尺度空間的影象,nOctaves為組數,nOctaveLayers即為我們定義的S。
2.3 為什麼是倒數第3張
相信你在看很多SIFT演算法描述裡都這樣寫著,取上一張的倒數第3張影象隔行取樣後作為下一組的第一張影象。
答案是為了保證尺度空間的連續性,我們下面來仔細分析。
我們知道對於尺度空間第o組,第s層的影象,它的尺度為$\sigma = \sigma_o k^{o+s/S},其中,k =1/2,o\in[0,1,2,\dots,nOctave-1],s\in[0,1,2,\dots,S+2]$。那麼我們從第0組開始,看它各層的尺度。
第0組:$\sigma_o \to 2^{1/3}\sigma_0\to 2^{2/3}\sigma_0\to 2^{3/3}\sigma_0\to 2^{4/3}\sigma_0\to 2^{5/3}\sigma_0$
第1組:$2\sigma_o\to 2*2^{1/3}\sigma_0\to 2*2^{2/3}\sigma_0\to 2*2^{3/3}\sigma_0\to 2*2^{4/3}\sigma_0\to 2*2^{5/3}\sigma_0$
我們只分析2組便可以看出,第1組的第0層影象恰好與第0組的倒數第三幅影象一致,尺度都為$2\sigma_0$,所以我們不需要再根據原圖來重新卷積生成每組的第0張影象,只需採用上一層的倒數第3張來降取樣即可。
我們也可以繼續分析,第0組尺度空間得到的高斯差分影象的尺度為:$\sigma_o\to 2^{1/3}\sigma_0\to 2^{2/3}\sigma_0\to 2^{3/3}\sigma_0\to 2^{4/3}\sigma_0$
而第1組尺度空間得到的高斯差分影象的尺度為:$2\sigma_o\to 2*2^{1/3}\sigma_0\to 2*2^{2/3}\sigma_0\to 2*2^{3/3}\sigma_0\to 2*2^{4/3}\sigma_0$
如果我們把它們的中間三項取出來拼在一起,則尺度為:$2^{1/3}\sigma_0\to 2^{2/3}\sigma_0\to 2^{3/3}\sigma_0\to 2*2^{1/3}\sigma_0\to 2*2^{2/3}\sigma_0\to 2*2^{3/3}\sigma_0$,正好連續!!這一效果帶來的直接的好處是在尺度空間的極值點確定過程中,我們不會漏掉任何一個尺度上的極值點,而是能夠綜合考慮量化的尺度因子。
2.4 用第i-1層的影象生成第i層的影象
值得注意的是,在SITF的原始碼裡,尺度空間裡的每一層的影象(除了第1層)都是由其前面一層的影象和一個相對$sigma$的高斯濾波器卷積生成,而不是由原圖和對應尺度的高斯濾波器生成的,這一方面是因為我前面提到的不存在所謂意思上的“原圖”,我們的輸入影象$I(x,y)$已經是尺度為$\sigma = 0.5$的影象了。另一方面是由於如果用原圖計算,那麼相鄰兩層之間相差的尺度實際上非常小,這樣會造成在做高斯差分影象的時候,大部分值都趨近於0,以致於後面我們很難檢測到特徵點。
基於上面兩點原因(個人認為原因1是最主要的,原因2只是根據實際嘗試後的一個猜想,並無理論依據),所以對於每一組的第$i+1$層的影象,都是由第$i$層的影象和一個相對尺度的高斯濾波器卷積生成。
那麼相對尺度如何計算呢,我們首先考慮第0組,它們的第$i+1$層影象與第$i$層影象之間的相對尺度為$SigmaDiff_i = \sqrt{(\sigma_0k^{i+1})^2 – (\sigma_0 k^i)^2}$,為了保持尺度的連續性,後面的每一組都用這樣一樣相對尺度(SIFT實際程式碼裡是這樣做的)。這裡有一個猜測,比如說尺度為$2\sigma_0$的這一組,第$i$層與第$i+1$層之間的相對尺度計算的結果應該為$\sqrt{(2\sigma_0k^{i+1})^2 – (2\sigma_0 k^i)^2} = 2\cdot SigmaDiff_i$,可是程式碼裡依然用$SigmaDiff_i$是因為這一層被降維了。
sig[0] = sigma; double k = pow(2., 1. / nOctaveLayers); for (int i = 1; i < nOctaveLayers + 3; i++) { double sig_prev = pow(k, (double)(i - 1))*sigma; double sig_total = sig_prev*k; sig[i] = std::sqrt(sig_total*sig_total - sig_prev*sig_prev); }
3. 特徵點的搜尋
3.1 搜尋策略
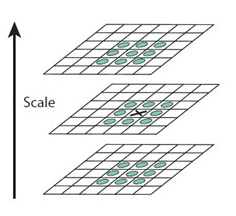
斑點的搜尋是通過同一組內各DoG相鄰層之間比較完成的。為了尋找尺度空間的極值點,每一個取樣點要和它所有的相鄰點進行比較,看其是否比它的影象域和尺度域的相鄰點大或小。對於其中的任意一個檢測點都要和它同尺度的8個相鄰點和上下相鄰尺度對應的$9\times2$個點共26個點比較,以確保在尺度空間和二維影象位置空間都檢測到極值點。也就是,比較是在一個$3\times3$的立方體內進行。
搜尋過程從每組的第二層開始,以第二層為當前層,對第二層的DoG影象中的每個點取一個$3\times3$的立方體,立方體上下層為第一層與第三層。這樣,搜尋得到的極值點既有位置座標(DoG的影象座標),又有空間尺度座標(層座標)。當第二層搜尋完成後,再以第三層作為當前層,其過程與第二層的搜尋類似。當S=3時,每組裡面要搜尋3層。
3.2 子像元插值
上的的極值點的搜尋是在離散空間中進行的,檢測到的極值點並不是真正意義上的極值點。下圖顯示了一維訊號離散空間得到的極值點與連續空間的極值點之間的差別。利用已知的離散空間點插值到連續空間極值點的方法叫子像元插值。
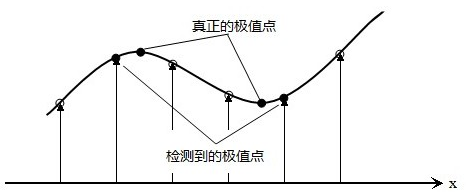
首先我們來看一個一維函式插值的例子。我們已經$f(x)$上幾個點的函式值$f(-1) = 1,f(0) = 6,f(1) = 5$,求$f(x)$在$[-1,1]$上的最大值。
如果我們只考慮離散的情況,那麼只用簡單比較一下,便知最大值為$f(0) = 6$,下面我們用子像元插值法來考慮連續區間的上情況:
利用泰勒級數,可以將$f(x)$在$f(0)$附近展開為:
$$f(x) \approx f(0) + f’(0)x+\frac{f’’(0)}{2}x^2$$
另外我們知道$f(x)$在$x$處的導數寫成離散的形式為$f’(x) = \frac{f(x+1) – f(x)}{2}$,二階導數寫成離散形式為$f’’(x) = f(x+1)+f(x-1)-2f(x)$。
所以,我們可以算出$f(x) \approx 6+2x+\frac{-6}{2}x^2 = 6+2x-3x^2$
求取函式$f(x)$的極大值和極大值所在的位置:
$$f’(x) = 2-6x = 0, \ \ \ \hat{x} = \frac{1}{3}$$
$$f(\hat{x}) = 6+2\times \frac{1}{3} – 3\times(\frac{1}{3})^2 = 6\frac{1}{3}$$
現在回到我們SIFT點檢測中來,我們要考慮的是一個三維問題,假設我們在尺度為$\sigma$的尺度影象$D(x,y)$上檢測到了一個區域性極值點,空間位置為$(x,y,\sigma)$,由上面的分析我們知道,它只是一個離散情況下的極值點,連續情況下,極值點可能落在了$(x,y,\sigma)$的附近,設其偏離了$(x,y,\sigma)$的座標為$(\Delta x,\Delta y,\Delta \sigma)$。則對$D(\Delta x,\Delta y,\Delta\sigma)$可以表示為在點$(x,y,\sigma)$處的泰勒展開:
$$D(\Delta x,\Delta y,\Delta \sigma) = D(x,y,\sigma)+\begin{bmatrix}
\frac{\partial D}{x} & \frac{\partial D}{y} & \frac{\partial D}{\sigma}
\end{bmatrix}\begin{bmatrix}
\Delta x\\
\Delta y\\
\Delta \sigma
\end{bmatrix}+\frac{1}{2}\begin{bmatrix}
\Delta x &\Delta y & \Delta \sigma
\end{bmatrix}\begin{bmatrix}
\frac{\partial ^2D}{\partial x^2} & \frac{\partial ^2D}{\partial x\partial y} &\frac{\partial ^2D}{\partial x\partial \sigma} \\
\frac{\partial ^2D}{\partial y\partial x}& \frac{\partial ^2D}{\partial y^2} & \frac{\partial ^2D}{\partial y\partial \sigma}\\
\frac{\partial ^2D}{\partial \sigma\partial x}&\frac{\partial ^2D}{\partial \sigma\partial y} & \frac{\partial ^2D}{\partial \sigma^2}
\end{bmatrix}\begin{bmatrix}
\Delta x\\
\Delta y\\
\Delta \sigma
\end{bmatrix}$$
可以將上式寫成向量形式如下:
$$D(x) = D+\frac{\partial D^T}{\partial x}\Delta x+\frac{1}{2}\Delta x^T\frac{\partial ^2D^T}{\partial x^2}\Delta x$$
令上式的一階導數等於0,可以求得$\Delta x = -\frac{\partial^2D^{-1}}{\partial x^2}\frac{\partial D(x)}{\partial x}$
通過多次迭代(Lowe演算法裡最多迭代5次),得到最終候選點的精確位置與尺度$\hat{x}$,將其代入公式求得$D(\hat{x})$,求其絕對值得$|D(\hat{x})|$。如果其絕對值低於閾值的將被刪除。
Vec3f dD((img.at<sift_wt>(r, c + 1) - img.at<sift_wt>(r, c - 1))*deriv_scale, (img.at<sift_wt>(r + 1, c) - img.at<sift_wt>(r - 1, c))*deriv_scale, (next.at<sift_wt>(r, c) - prev.at<sift_wt>(r, c))*deriv_scale); // dD為一階差分向量Df/Dx float v2 = (float)img.at<sift_wt>(r, c) * 2; float dxx = (img.at<sift_wt>(r, c + 1) + img.at<sift_wt>(r, c - 1) - v2)*second_deriv_scale; float dyy = (img.at<sift_wt>(r + 1, c) + img.at<sift_wt>(r - 1, c) - v2)*second_deriv_scale; float dss = (next.at<sift_wt>(r, c) + prev.at<sift_wt>(r, c) - v2)*second_deriv_scale; float dxy = (img.at<sift_wt>(r + 1, c + 1) - img.at<sift_wt>(r + 1, c - 1) - img.at<sift_wt>(r - 1, c + 1) + img.at<sift_wt>(r - 1, c - 1))*cross_deriv_scale; float dxs = (next.at<sift_wt>(r, c + 1) - next.at<sift_wt>(r, c - 1) - prev.at<sift_wt>(r, c + 1) + prev.at<sift_wt>(r, c - 1))*cross_deriv_scale; float dys = (next.at<sift_wt>(r + 1, c) - next.at<sift_wt>(r - 1, c) - prev.at<sift_wt>(r + 1, c) + prev.at<sift_wt>(r - 1, c))*cross_deriv_scale; Matx33f H(dxx, dxy, dxs, dxy, dyy, dys, dxs, dys, dss); // dD + Hx = 0 --> x = H^-1 * (-dD) Vec3f X = H.solve(dD, DECOMP_LU);
3.3 刪除邊緣效應
為了得到穩定的特徵點,只是刪除DoG響應值低的點是不夠的。由於DoG對影象中的邊緣有比較強的響應值,而一旦特徵點落在影象的邊緣上,這些點就是不穩定的點。一方面影象邊緣上的點是很難定位的,具有定位歧義性;另一方面這樣的點很容易受到噪聲的干擾而變得不穩定。
一個平坦的DoG響應峰值往往在橫跨邊緣的地方有較大的主曲率,而在垂直邊緣的方向有較小的主曲率。而主曲率可以通過$2\times2$的Hessian矩陣$H$求出:
$$H(x,y) = \begin{bmatrix}D_{xx}(x,y) & D_{xy}(x,y)\\ D_{xy}(x,y) &D_{yy}(x,y) \end{bmatrix}$$
上式中,$D$值可以通過求取鄰近點畫素的差分得到。$H$的特徵值與$D$的主曲率成正比例。我們可以避免求取具體的特徵值,因為我們只關心特徵值的比例。令$\alpha = \lambda_{max}$為最大的特徵值,$\beta = \lambda_{min}$為最小的特徵值,那麼,我們通過$H$矩陣直跡計算它們的和,通過$H$矩陣的行列式計算它們的乘積:
$$Tr(H) = D_{xx}+D_{yy} = \alpha +\beta$$
$$Det(H) = D_{xx}D_{yy}-(D_{xy})^2=\alpha \beta$$
如果$\gamma$為最大特徵值與最小特徵值之間的比例,那麼$\alpha = \gamma \beta$,這樣便有
$$\frac{Tr(H)^2}{Det(H)} = \frac{(\alpha+\beta)^2}{\alpha\beta} = \frac{(\gamma+1)^2}{\gamma}$$
上式的結果只與兩個特徵值的比例有關,而與具體特徵值無關。當兩個特徵值相等時,$\frac{(\gamma+1)^2}{\gamma}$的值最小,隨著$\gamma$的增加,$\frac{(\gamma+1)^2}{\gamma}$的值也增加。所以要想檢查主曲率的比例小於某一閾值$\gamma$,只要檢查下式是否成立:
$$\frac{Tr(H)^2}{Det(H)} < \frac{(\gamma+1)^2}{\gamma}$$
Lowe在論文中給出的$\gamma = 10$。也就是說對於主曲率比值大於10的特徵點將被刪除。
float t = dD.dot(Matx31f(xc, xr, xi)); //D(\bar{x}) = D + 1/2*dD*\bar{x} contr = img.at<sift_wt>(r, c)*img_scale + t * 0.5f; // 插值得到的極值點的值 if (std::abs(contr) * nOctaveLayers < contrastThreshold) return false; // principal curvatures are computed using the trace and det of Hessian float v2 = img.at<sift_wt>(r, c)*2.f; float dxx = (img.at<sift_wt>(r, c + 1) + img.at<sift_wt>(r, c - 1) - v2)*second_deriv_scale; float dyy = (img.at<sift_wt>(r + 1, c) + img.at<sift_wt>(r - 1, c) - v2)*second_deriv_scale; float dxy = (img.at<sift_wt>(r + 1, c + 1) - img.at<sift_wt>(r + 1, c - 1) - img.at<sift_wt>(r - 1, c + 1) + img.at<sift_wt>(r - 1, c - 1)) * cross_deriv_scale; float tr = dxx + dyy; float det = dxx * dyy - dxy * dxy; if (det <= 0 || tr*tr*edgeThreshold >= (edgeThreshold + 1)*(edgeThreshold + 1)*det) return false;