一個隱馬爾科夫模型的應用例項：中文分詞

什麼問題用HMM解決

現實生活中有這樣一類隨機現象，在已知現在情況的條件下，未來時刻的情況只與現在有關，而與遙遠的過去並無直接關係。

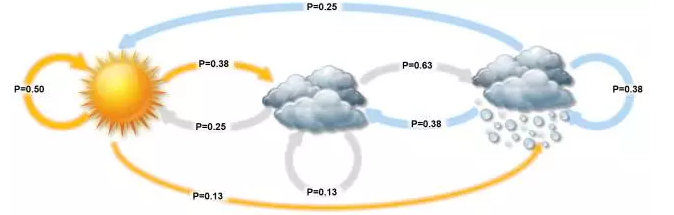
比如天氣預測，如果我們知道“晴天，多雲，雨天”之間的轉換概率，那麼如果今天是晴天，我們就可以推斷出明天是各種天氣的概率，接著後天的天氣可以由明天的進行計算。這類問題可以用 Markov 模型來描述。

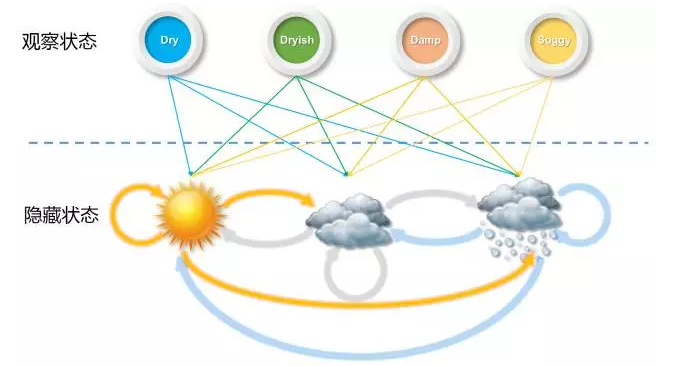
進一步，如果我們並不知道今天的天氣屬於什麼狀況，我們只知道今明後三天的水藻的乾燥溼潤狀態，因為水藻的狀態和天氣有關，我們想要通過水藻來推測這三天的真正的天氣會是什麼，這個時候就用 Hidden Markov 模型來描述。

HMM 模型的本質是從觀察的引數中獲取隱含的引數資訊，並且前後之間的特徵會存在部分的依賴影響。

我們從如何進行中文分詞的角度來理解HMM

根據可觀察狀態的序列找到一個最可能的隱藏狀態序列

中文分詞，就是給一個漢語句子作為輸入，以“BEMS”組成的序列串作為輸出，然後再進行切詞，進而得到輸入句子的劃分。其中，B代表該字是詞語中的起始字，M代表是詞語中的中間字，E代表是詞語中的結束字，S則代表是單字成詞。

例如：給個句子

小明碩士畢業於中國科學院計算所

得到BEMS組成的序列為

BEBEBMEBEBMEBES

因為句尾只可能是E或者S，所以得到切詞方式為

BE/BE/BME/BE/BME/BE/S

進而得到中文句子的切詞方式為

小明/碩士/畢業於/中國/科學院/計算/所

這是個HMM問題，因為你想要得到的是每個字的位置，但是看到的只是這些漢字，需要通過漢字來推出每個字在詞語中的位置，並且每個字屬於什麼狀態還和它之前的字有關。
此時，我們需要根據可觀察狀態的序列找到一個最可能的隱藏狀態序列。

五元組，三類問題，兩個假設

五元組

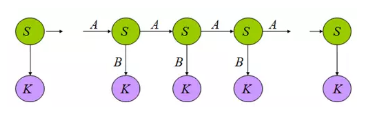
通過上面的例子，我們可以知道 HMM 有以下5個要素。

觀測序列－O：小明碩士畢業於中國科學院計算所

狀態序列－S：BEBEBMEBEBMEBES

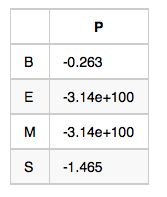
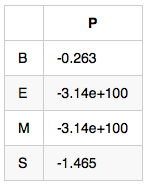
初始狀態概率向量－π：句子的第一個字屬於{B,E,M,S}這四種狀態的概率

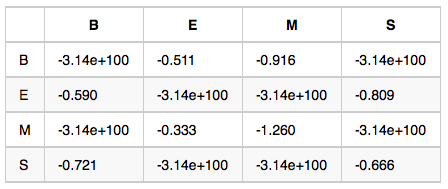
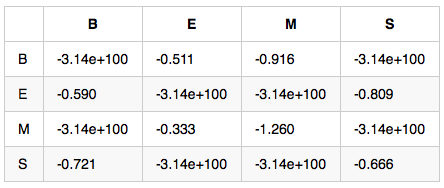
狀態轉移概率矩陣－A：如果前一個字位置是B，那麼後一個字位置為BEMS的概率各是多少

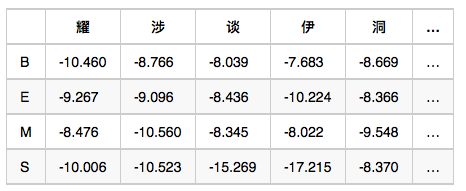
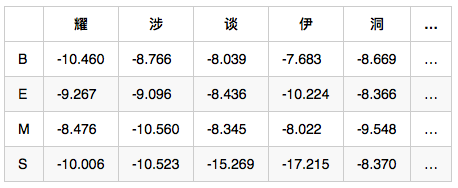
觀測概率矩陣－B：在狀態B的條件下，觀察值為耀的概率，取對數後是-10.460

備註：示例數值是對概率值取對數之後的結果，為了將概率相乘的計算變成對數相加，其中-3.14e+100作為負無窮，也就是對應的概率值是0

三類問題

當通過五元組中某些已知條件來求未知時，就得到HMM的三類問題：

• 似然度問題：引數(O，π，A，B)已知的情況下，求(π，A，B)下觀測序列O出現的概率。(Forward-backward演算法)
• 解碼問題：引數(O，π，A，B)已知的情況下，求解狀態值序列S。(viterbi演算法)
• 學習問題：引數(O)已知的情況下，求解(π，A，B)。(Baum-Welch演算法)

中文分詞這個例子屬於第二個問題，即解碼問題。

我們希望找到 s_1,s_2,s_3,… 使 P (s_1,s_2,s_3,…|o_1,o_2,o_3….) 達到最大。
意思是，當我們觀測到語音訊號 o_1,o_2,o_3,… 時，我們要根據這組訊號推測出傳送的句子 s_1,s_2,s_3,….，顯然，我們應該在所有可能的句子中找最有可能性的一個。

兩個假設

利用貝葉斯公式得到：

這裡需要用到兩個假設來進一步簡化上述公式

有限歷史性假設: si 只由 si-1 決定

獨立輸出假設：第 i 時刻的接收訊號 oi 只由傳送訊號 si 決定

有了上面的假設，就可以利用演算法 Viterbi 找出目標概率的最大值。

Viterbi演算法

根據動態規劃原理，最優路徑具有這樣的特性：如果最優路徑從結點 i_{t}^ 到終點 i_{T}^，那麼這兩點之間的所有可能的部分路徑必須是最優的。
依據這一原理，我們只需從時刻 t=1 開始，遞推地計算在時刻 t 狀態為 i 的各條部分路徑的最大概率，直至得到時刻 t=T 狀態為 i 的各條路徑的最大概率 P^，最優路徑的終結點 i_{T}^ 也同時得到。之後，為了找出最優路徑的各個結點，從終結點 i_{T}^ 開始，由後向前逐步求得結點 i_{T-1}^…，i_{1}^，進而得到最優路徑 I^＝i_{1}^…，i_{T}^，這就是維特比演算法.

舉個例子：

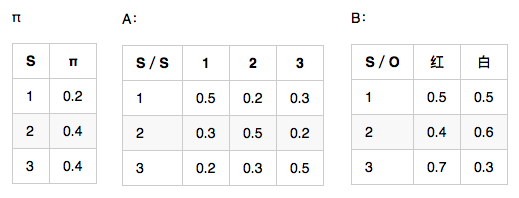
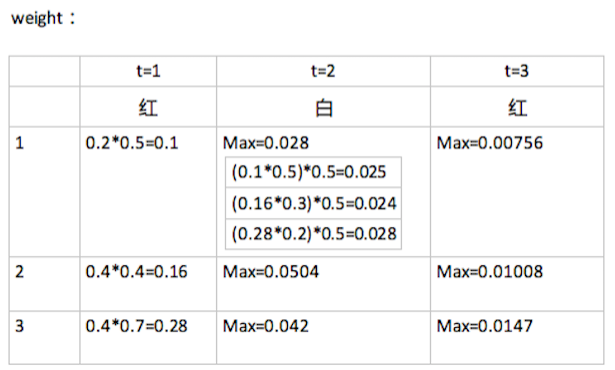
觀測序列 O＝(紅，白，紅)，想要求狀態序列S。

需要定義兩個變數:

• weight[3][3]，行3是狀態數(1，2，3)，列3是觀察值個數(紅，白，紅)。意思是，在時刻 t 狀態為 i 的所有單個路徑中的概率最大值。
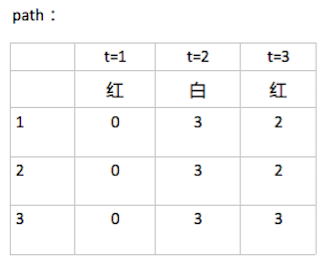
• path[3][3]，意思是，在時刻 t 狀態為 i 的所有單個路徑中概率最大的那條路徑，它的第 t-1 個結點是什麼。比如 path[0][2]=1, 則代表 weight[0][2] 取到最大時，前一個時刻的狀態是 1.

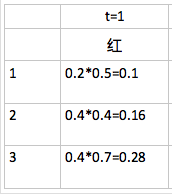
1.初始化

t＝1 時的紅，分別是在狀態 1，2，3 的條件下觀察得來的概率計算如下：

此時 path 的第一列全是 0.

2.遞迴

t＝2 時的白，如果此時是在 1 的條件下觀察得來的話，先計算此時狀態最可能是由前一時刻的哪個狀態轉換而來的，取這個最大值，再乘以 1 條件下觀測到 白 的概率，同時記錄 path矩陣：如下圖 weight[0][1]=0.028，此值來源於前一時刻狀態是3，所以，

3.終止

在 t＝3 時的最大概率 P^＝0.0147，相應的最優路徑的終點是 i_3^=3.

4.回溯

由最優路徑的終點 3 開始，向前找到之前時刻的最優點：

• 在 t＝2 時，因 i_3^=3，狀態 3 的最大概率 P＝0.0147，來源於狀態 3，所以 i_2^=3.
• 在 t＝1 時，因 i_2^=3，狀態 3 的最大概率 P＝0.042，來源於狀態 3，所以 i_1^=3.

最後得到最優路徑為 I^＝(i_{1}^，i_{2}^，i_{3}^)＝(3,3,3)

用Viterbi演算法求解中文分詞問題

根據上面講的 HMM 和 Viterbi，接下來對中文分詞這個問題，構造五元組並用演算法進行求解。

InitStatus：π

TransProbMatrix：A

EmitProbMatrix：B

Viterbi求解

經過這個演算法後，會得到兩個矩陣 weight 和 path：

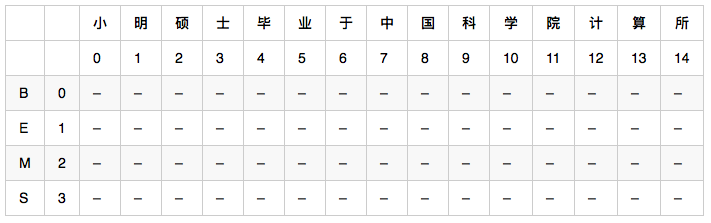
二維陣列 weight[4][15]，4是狀態數(0:B,1:E,2:M,3:S)，15是輸入句子的字數。比如 weight[0][2] 代表 狀態B的條件下，出現’碩’這個字的可能性。

二維陣列 path[4][15]，4是狀態數(0:B,1:E,2:M,3:S)，15是輸入句子的字數。比如 path[0][2] 代表 weight[0][2]取到最大時，前一個字的狀態，比如 path[0][2] = 1, 則代表 weight[0][2]取到最大時，前一個字(也就是明)的狀態是E。記錄前一個字的狀態是為了使用viterbi演算法計算完整個 weight[4][15] 之後，能對輸入句子從右向左地回溯回來，找出對應的狀態序列。

先對 weight 進行初始化，

使用 InitStatus 和 EmitProbMatrix 對 weight 二維陣列進行初始化。

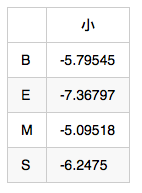
由 EmitProbMatrix 可以得出

所以可以初始化 weight[i][0] 的值如下：

注意上式計算的時候是相加而不是相乘，因為之前取過對數的原因。

然後遍歷找到 weight 每項的最大值，同時記錄了相應的 path

//遍歷句子，下標i從1開始是因為剛才初始化的時候已經對0初始化結束了
for(size_t i = 1; i < 15; i++)
{
    // 遍歷可能的狀態
    for(size_t j = 0; j < 4; j++) 
    {
        weight[j][i] = MIN_DOUBLE;
        path[j][i] = -1;
        //遍歷前一個字可能的狀態
        for(size_t k = 0; k < 4; k++)
        {
            double tmp = weight[k][i-1] + _transProb[k][j] + _emitProb[j][sentence[i]];
            if(tmp > weight[j][i]) // 找出最大的weight[j][i]值
            {
                weight[j][i] = tmp;
                path[j][i] = k;
            }
        }
    }
}

如此遍歷下來，weight[4][15] 和 path[4][15] 就都計算完畢。

確定邊界條件和路徑回溯

邊界條件如下：

對於每個句子，最後一個字的狀態只可能是 E 或者 S，不可能是 M 或者 B。
所以在本文的例子中我們只需要比較 weight[1(E)][14] 和 weight[3(S)][14] 的大小即可。

在本例中：

weight[1][14] = -102.492;

weight[3][14] = -101.632;

所以 S > E，也就是對於路徑回溯的起點是 path[3][14]。

進行回溯，得到序列

SEBEMBEBEMBEBEB。

再進行倒序，得到

BEBEBMEBEBMEBES

接著進行切詞得到

BE/BE/BME/BE/BME/BE/S

最終就找到了分詞的方式

小明/碩士/畢業於/中國/科學院/計算/所

HMM還有哪些應用

HMM不只用於中文分詞，如果把 S 換成句子，O 換成語音訊號，就變成了語音識別問題，如果把 S 換成中文，O 換成英文，就變成了翻譯問題，如果把 S 換成文字，O 換成影像，就變成了文字識別問題，此外還有詞性標註等等問題。

對於上述每種問題，只要知道了五元組中的三個引數矩陣，就可以應用 Viterbi 演算法得到結果。