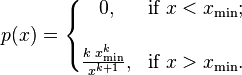Common Probability Distributions

Common Probability Distributions

Probability Distribution

A probability distribution describes the probabilities of all the possible outcomes for a random variable.

A discrete random variable if one for which the number of possible outcomes can be counted, and for each possible outcome, there is a measurable and positive probability.

A continuous random variable is one for which the number of possible outcome is infinite, even if lower and upper bounds exist.

A cumulative distribution function (CDF) defines the probability that a random variable, X, takes on a value equal to or less than a specific value, x.

F(x)=P(X<=x)

A discrete uniform random variable is one for which the probabilities for all possible outcomes for a discrete random variable are equal.

Binomial Distribution(二項分佈)

A binomial random variable may be defined as the number of "success" in a given number of trials, whereby the outcome can be either "success" or "failure". The probability of success, p, is constant for each trial, and the trails are independent.

Note: binomial distribution is a discrete distribution.

A binomial random variable for which the number of trials is 1 is called Bernoulli random variable (伯努利隨即變數).

Expected value

For a given serial of n trials,, the expected number of success, or E(X), is given by the following formula:

expectedd value of X = E(X) = np

The intuition is straightforward; if we perform n trails and the probability of success on each trail is p, we expect np successes.

Variance

The variance of a binomial random variable is given by:

variance of X = np(1-p)

Tracking Error

Tracking error is the difference between the total return on a portfolio and the total return on the benchmark against which its performance is measured.

Note: The expression "tracking error" is sometimes used interchangeably with "tracking risk", which refer to the standard deviation of the differences between a portfolio's return and its benchmark return.

Continuous Uniform Distribution

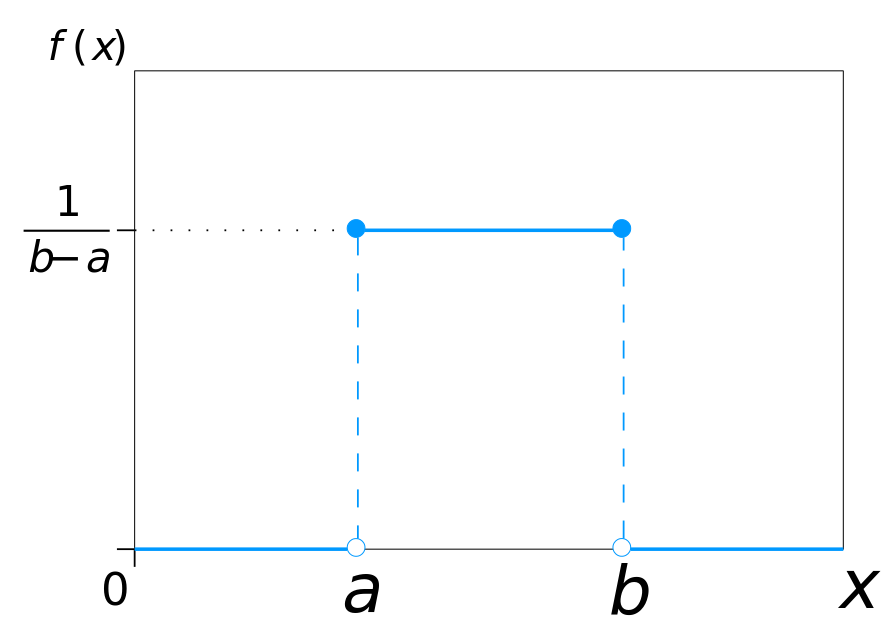
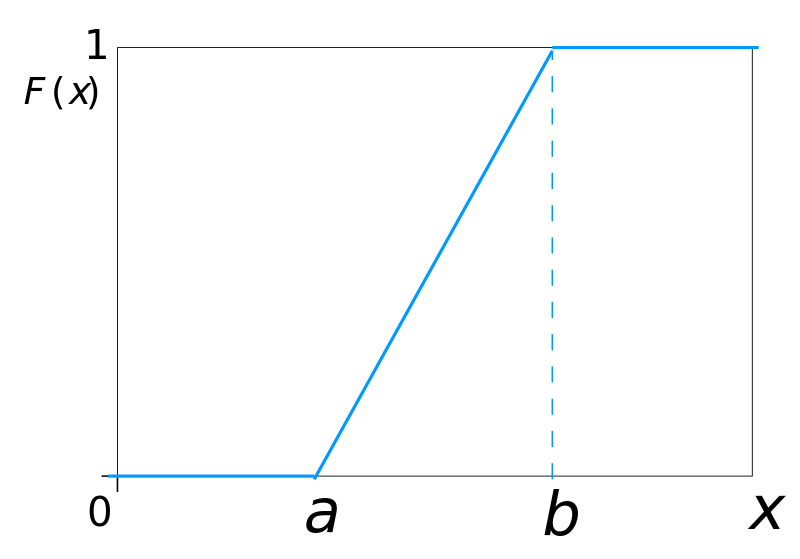
The continuous uniform distribution is defined over a range that spans between some lower limit, a, and some upper limit, b, which serve as the parameters of the distribution. Outcomes can only occur between a and b, and since we are dealing with a continuous distribution, even if a < x < b, P(X=x)=0.

• PDF (probability density function)
  

• CDF (continuous distribution function)
  

Normal Distribution

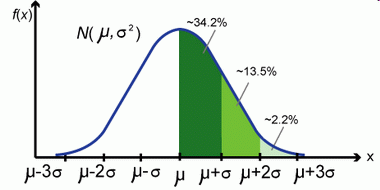
Note: some properties of normal distribution:

1. Skewness=0
2. Kurtosis=3
3. A linear combination of normally distributed random variables is also normally distributed.

Standard Normal Distribution (標準正太分佈) and Z value

The standard normal distribution is a normal distribution that has been standardized so that is has a mean of zero and a standard deviation of 1.

To standardize an observation from a given normal distribution,, the z-value of the observation must be calculated. The z-value represents the number of standard deviations a given observation is from the population mean. Standardization is the process of converting an observed value for a random variable to its z-value.

z = [observation-population mean]/[standard deviation] = [x-μ]/σ

Confidence Interval(置信區間）

A confidence interval is a range of values around the expected outcome within which we expect the actual outcome to be some specified percentage of the time. A 95% confidence interval is a range that we expect the random variable to be in 95% of time. For a normal distribution, this interval is based on the expected value(sometimes called a point estimate) of the random variable and on its variability, which we measure with standard deviation.

Note: 1-confidence interval = α (which is called significance level)

For any normally distributed random variable, 68% of outcomes are within one standard deviation of the expected value (mean), and approximately 95% of the outcomes are within two standard deviations of the expected value.

Shortfall risks, Safety-First ratio

Shortfall risk　is the probability that a portfolio value or return will fall below a particular(target) value or return over a given time period.

Roy's safety-first criterion states that the optimal portfolio minimizes the probability that the return of the portfolio falls below some minimum acceptable level. This minimum acceptable level is called the threshold level.

If portfolio returns area normally distributed, then Roy's safety-first criterion can be stated as:

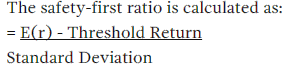
Note that the SFR is the number of standard deviations below the mean. Thus the portfolio with the larger SFR has the lower probability of returns below the threshold return.

Lognormal distribution(對數正太分佈)

The lognormal distribution is generated by the function e^x, where x is normally distributed. Since the natural logarithm, ln, of e^x is x, the logarithms of lognormally distributed random variables are normally distributed.

• The log-normal distribution is skewed to the right
• The log-normal distribution is bounded from below by zero that it is useful for modeling asset prices which never take negative values.

PMF(Probability Mass Function)

PMF(概率質量函式)，這個函式是值到其概率的對映。

如果要處理的資料比較少，PMF很合適。但隨著資料的增加，每個值的概率就會降低，而隨機噪聲的影響就會增大。

CDF(Cumulative Distribution Function)

CDF(累積分佈函式), 這個函式是值到其在分佈中百分等級的對映。

  def Cdf(t, x):
     count = 0.0
     for value in t:
        if value <= x:
           count += 1.0
     prob = count / len(t)
     return prob

我們可以計算任意值x的CDF， 而不僅僅是樣本中出現的值。如果x比樣本中最小的值還要小，那麼CDF(x)就等於0.如果x比樣本中的最大值還要大，那麼CDF(x)就是1.

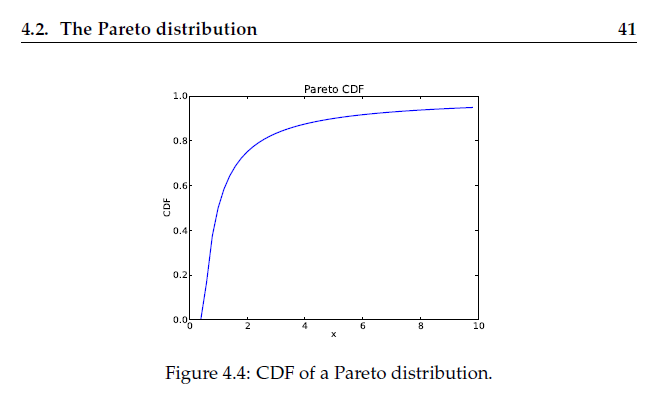
帕累託分佈

See百度百科 and 維基百科

帕累託分佈(Pareto distribution)是以義大利經濟學家維弗雷多·帕雷託命名的。 是從大量真實世界的現象中發現的冪次定律分佈。這個分佈在經濟學以外，也被稱為布拉德福分佈。

帕累託因對義大利20%的人口擁有80%的財產的觀察而著名，後來被約瑟夫·朱蘭和其他人概括為帕累托法則（80/20法則），後來進一步概括為帕累託分佈的概念。

在帕累託分佈中，如果X是一個隨機變數， 則X的概率分佈如下面的公式所示：

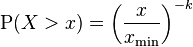
其中x是任何一個大於xmin的數，xmin是X最小的可能值（正數），k是為正的引數。帕累託分佈曲線族是由兩個數量引數化的：xmin和k。分佈密度則為