KCF目標跟蹤方法分析與總結
讀"J. F. Henriques, R. Caseiro, P. Martins, J. Batista, 'High-speed tracking with kernelized correlation filters'" 筆記
KCF是一種鑑別式追蹤方法,這類方法一般都是在追蹤過程中訓練一個目標檢測器,使用目標檢測器去檢測下一幀預測位置是否是目標,然後再使用新檢測結果去更新訓練集進而更新目標檢測器。而在訓練目標檢測器時一般選取目標區域為正樣本,目標的周圍區域為負樣本,當然越靠近目標的區域為正樣本的可能性越大。
注意論文中關於向量是行向量還是列向量總是指示不清楚,所以本文對變數符號統一之後進行推導,首先所有的小寫字母均表示列向量,所有的大寫字母表示矩陣,其中矩陣的每一行是一個樣本,文中的函式除了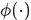 是對行向量操作,其餘都是對元素操做的,四則運算子號也都是針對元素操作的。還有所有對迴圈矩陣使用傅立葉變換時使用的生成向量都是迴圈矩陣的第一行向量,這點很重要。
是對行向量操作,其餘都是對元素操做的,四則運算子號也都是針對元素操作的。還有所有對迴圈矩陣使用傅立葉變換時使用的生成向量都是迴圈矩陣的第一行向量,這點很重要。
KCF的主要貢獻
使用目標周圍區域的迴圈矩陣採集正負樣本,利用脊迴歸訓練目標檢測器,併成功的利用迴圈矩陣在傅立葉空間可對角化的性質將矩陣的運算轉化為向量的Hadamad積,即元素的點乘,大大降低了運算量,提高了運算速度,使演算法滿足實時性要求。
將線性空間的脊迴歸通過核函式對映到非線性空間,在非線性空間通過求解一個對偶問題和某些常見的約束,同樣的可以使用迴圈矩陣傅立葉空間對角化簡化計算。
給出了一種將多通道資料融入該演算法的途徑。
一維脊迴歸
脊迴歸
設訓練樣本集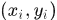 ,那麼其線性迴歸函式
,那麼其線性迴歸函式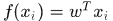 ,
,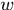 是列向量表示權重係數,可通過最小二乘法求解
是列向量表示權重係數,可通過最小二乘法求解
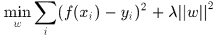
其中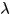 用於控制系統的結構複雜性,也就是VC維以保證分類器的泛化效能。
用於控制系統的結構複雜性,也就是VC維以保證分類器的泛化效能。
寫成矩陣形式
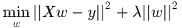
其中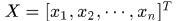 的每一行表示一個向量,
的每一行表示一個向量,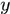 是列向量,每個元素對應一個樣本的標籤,於是令導數為0,可求得
是列向量,每個元素對應一個樣本的標籤,於是令導數為0,可求得
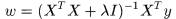
因為後面實在傅立葉域內計算,牽涉到複數矩陣,所以我們將結果都統一寫成複數域中形式

其中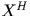 表示複共軛轉置矩陣。
表示複共軛轉置矩陣。
迴圈矩陣
KCF中所有的訓練樣本是由目標樣本迴圈位移得到的,向量的迴圈可有排列矩陣得到,比如
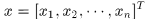


當然對於二維影像的話,可以通過x軸和y軸分別迴圈移動實現不同位置的移動

舉例


所以由一個向量 可以通過不斷的乘上排列矩陣得到n個迴圈移位向量,將這n個向量依序排列到一個矩陣中,就形成了x生成的迴圈矩陣,表示成
可以通過不斷的乘上排列矩陣得到n個迴圈移位向量,將這n個向量依序排列到一個矩陣中,就形成了x生成的迴圈矩陣,表示成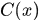
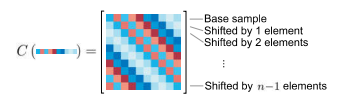

迴圈矩陣傅氏空間對角化
所有的迴圈矩陣都能夠在傅氏空間中使用離散傅立葉矩陣進行對角化
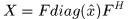
其中x對應於生成X的向量(就是X的第一行矩陣)的傅立葉變化後的值, ,
,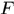 是離散傅立葉矩陣,是常量
是離散傅立葉矩陣,是常量
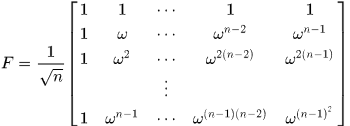
關於矩陣的傅立葉對角化請參加 迴圈矩陣傅立葉對角化,後面的筆記會專門講解傅立葉變換。
傅氏對角化簡化的脊迴歸
將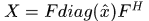 帶入脊迴歸公式得到
帶入脊迴歸公式得到
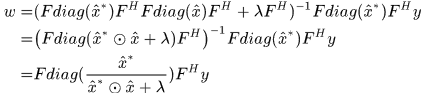
注意這裡的分號是點除運算,就是對應元素相除。因為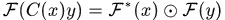 ,( 迴圈矩陣傅立葉對角化)對上式兩邊同時傅氏變換得
,( 迴圈矩陣傅立葉對角化)對上式兩邊同時傅氏變換得
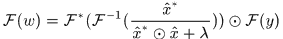
於是
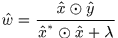
這裡和論文式(12)不一樣,論文裡(12)式分子上似乎多了個共軛符號,因為Appendix A.5中的式(55)後面那個 應該是少了個共軛轉置符號。
應該是少了個共軛轉置符號。
這樣就可以使用向量的點積運算取代矩陣運算,特別是求逆運算,大大提高了計算速度。

核空間的脊迴歸
我們希望找到一個非線性對映函式 列向量,使對映後的樣本在新空間中線性可分,那麼在新空間中就可以使用脊迴歸來尋找一個分類器
列向量,使對映後的樣本在新空間中線性可分,那麼在新空間中就可以使用脊迴歸來尋找一個分類器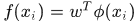 ,所以這時候得到的權重係數為
,所以這時候得到的權重係數為

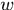 是
是 行向量張成的空間中的一個向量,所以可以令
行向量張成的空間中的一個向量,所以可以令
上式就變為
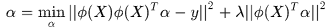
該問題稱為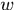 的對偶問題
的對偶問題
令關於列向量 導數為0,
導數為0,
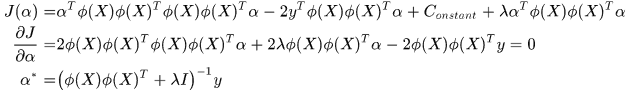
注: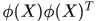 其實類似於核空間變數的協方差矩陣,矩陣的轉置乘以矩陣,一定可逆。
其實類似於核空間變數的協方差矩陣,矩陣的轉置乘以矩陣,一定可逆。
對於核方法,我們一般不知道非線性對映函式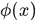 的具體形式,而只是刻畫在核空間的核矩陣
的具體形式,而只是刻畫在核空間的核矩陣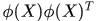 ,那麼我們令
,那麼我們令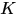 表示核空間的核矩陣,由核函式得到,那麼
表示核空間的核矩陣,由核函式得到,那麼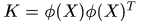
於是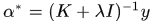
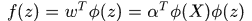
論文提出的一個創新點就是使迴圈矩陣的傅氏對角化簡化計算,所以這裡如果希望計算 時可以同樣將矩陣求逆運算變為元素運算,就希望將
時可以同樣將矩陣求逆運算變為元素運算,就希望將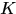 對角化,所以希望找到一個核函式使對應的核矩陣式迴圈矩陣。
對角化,所以希望找到一個核函式使對應的核矩陣式迴圈矩陣。
Theorem 1. Given circulant data C(x), the corresponding kernel matrix K is circulatant if the kernel function satisfies
,for any permutation matrix M.
即核矩陣是迴圈矩陣應該滿足兩個條件:第一個樣本和第二個樣本都是由生成樣本迴圈移位產生的,可以不是由同一個樣本生成;滿足,其中
是排列矩陣。
證明:設 ,則
,則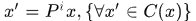 ,於是
,於是

因為K的第一行為 所以
所以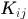 相當於將第一行的第
相當於將第一行的第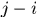 個元素放到K的第i行j列上,
個元素放到K的第i行j列上,
那麼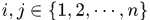 就得到了迴圈矩陣,所以
就得到了迴圈矩陣,所以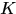 是迴圈矩陣。證明裡
是迴圈矩陣。證明裡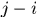 表示除
表示除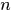 的餘數,因為這個過程是迴圈的。
的餘數,因為這個過程是迴圈的。
證畢。
若K是迴圈矩陣,則
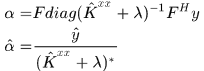
其中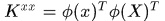 是K中第一行。這裡覺得奇怪?兩個轉置?這是因為我們已經約定
是K中第一行。這裡覺得奇怪?兩個轉置?這是因為我們已經約定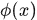 是列向量,而
是列向量,而 的第i行是
的第i行是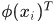 ,是不是明白了~
,是不是明白了~
這裡推出來的公式和論文中公式(17)也不大一樣
那麼那些核函式滿足上述性質呢?論文中給出
Radial Basis Function kernels -e.g. Gaussian
Dot-Product kernels -e.g. linear, polynomial
Additive kernels - e.g. intersection,
 and Hellinger kernels
and Hellinger kernelsExponentiated additive kernels.
快速檢測
首先由訓練樣本和標籤訓練檢測器,其中訓練集是由目標區域和由其移位得到的若干樣本組成,對應的標籤是根據距離越近正樣本可能性越大的準則賦值的,然後可以得到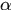
待分類樣本集,即待檢測樣本集,是由預測區域和由其移位得到的樣本集合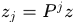
那麼就可以選擇 最大的樣本作為檢測出的新目標區域,由
最大的樣本作為檢測出的新目標區域,由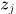 判斷目標移動的位置。
判斷目標移動的位置。
定義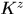 是測試樣本和訓練樣本間在核空間的核矩陣
是測試樣本和訓練樣本間在核空間的核矩陣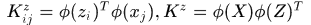
由於核矩陣滿足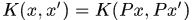 ,即
,即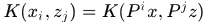 類似於theorem 1 的證明可得
類似於theorem 1 的證明可得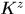 是迴圈矩陣
是迴圈矩陣
我記得曾經見到過有人問 非方陣的情況,假設取樣視窗非方形,即
非方陣的情況,假設取樣視窗非方形,即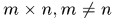 那麼取樣視窗通過移位都會產生
那麼取樣視窗通過移位都會產生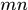 個樣本,無論是訓練樣本還是測試樣本,所以
個樣本,無論是訓練樣本還是測試樣本,所以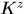 一定是方陣
一定是方陣
於是得到各個測試樣本的響應
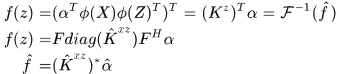
注意我們說過小寫的都是列向量,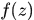 是列向量。注意我們這裡
是列向量。注意我們這裡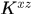 是矩陣
是矩陣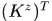 的第一行,即
的第一行,即 的第一列,而文中(22)式中
的第一列,而文中(22)式中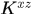 是論文中
是論文中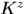 的第一行,這是因為本文和論文中關於
的第一行,這是因為本文和論文中關於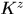 的定義正好是相轉置的。也就是說我覺得(22)式只是少了一個共軛。。。
的定義正好是相轉置的。也就是說我覺得(22)式只是少了一個共軛。。。
覺得蠻奇怪的,怎麼和論文中推導結果好多都差一個共軛符號??
這是因為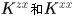 都是對稱向量,而對稱向量的共軛轉置是實數,所以就和論文中一樣了,這點參考KCF高速跟蹤詳解
都是對稱向量,而對稱向量的共軛轉置是實數,所以就和論文中一樣了,這點參考KCF高速跟蹤詳解
核矩陣的快速計算
現在還存在的矩陣運算就是核矩陣的第一行的計算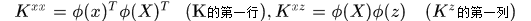
內積和多項式核
這種核函式核矩陣可以表示成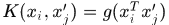 ,於是
,於是

因此對於多項式核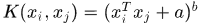 有
有
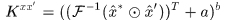
徑向基核函式
比如高斯核,這類函式是 的函式
的函式
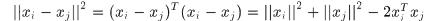
所以
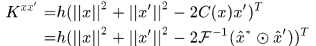
對於高斯核則有
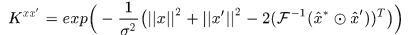
1D到2D
上面公式推導的很爽,可是都是在1D情況下得到了結論,2D影像該怎麼辦呢?
這個問題困擾了我好久。。。。剛開始我也想從線性空間的脊迴歸推導,假設 是目標影像,
是目標影像, 是由
是由 生成的迴圈矩陣塊,即
生成的迴圈矩陣塊,即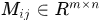 表示
表示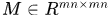 的第
的第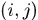 塊,是由
塊,是由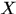 右移
右移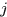 ,下移
,下移 得到的樣本塊。那麼即使塊迴圈矩陣能夠通過2D傅立葉變換矩陣對角化又怎麼用呢??因為我們不可能帶入
得到的樣本塊。那麼即使塊迴圈矩陣能夠通過2D傅立葉變換矩陣對角化又怎麼用呢??因為我們不可能帶入 類似的式子中啊(這個式子是類比於1D脊迴歸寫的,並無實際意義)
類似的式子中啊(這個式子是類比於1D脊迴歸寫的,並無實際意義)
哎呀,想破腦袋啊!
啊哈,想明白了,線性假設下沒辦法用,直接在核空間推導,發現豁然開朗~
現在有一個函式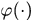 ,自變數
,自變數 ,因變數
,因變數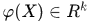 ,也不知道怎麼對映的,也不知道
,也不知道怎麼對映的,也不知道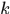 是多少,反正是個確定但未知的值。那麼在核空間我們就可以使用脊迴歸的公式了~
是多少,反正是個確定但未知的值。那麼在核空間我們就可以使用脊迴歸的公式了~

注意:由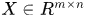 移位生成的樣本共有
移位生成的樣本共有 個,所以
個,所以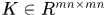 ,這裡
,這裡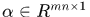 ,
,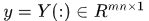 是對應樣本的標籤,
是對應樣本的標籤, 是對應樣本標籤的矩陣形式。
是對應樣本標籤的矩陣形式。
ok,現在再來看看定理2
Theorem 2. The block matrix
with elements
is a Block-Circulant Matrix (BCCM) if
is a unitarily invariant kernel.
這裡和Theorem 1是類似的,a unitarily invariant kernel就是說,定理的證明參見Theorem 1.
而徑向基核,dot-product kernel等都滿足這個條件,所以得到的核矩陣都是塊迴圈矩陣。
塊迴圈矩陣可以使用2D傅立葉變換矩陣對角化( 迴圈矩陣傅立葉對角化)
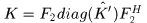
其中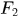 是2D傅立葉變換矩陣,
是2D傅立葉變換矩陣,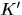 是生成塊迴圈矩陣
是生成塊迴圈矩陣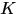 的生成矩陣,
的生成矩陣, 表示對
表示對 進行2D傅立葉變換的結果。
進行2D傅立葉變換的結果。
ok,那現在
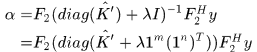
其中 表示全1的m維列向量。
表示全1的m維列向量。

這裡的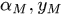 分別對應著
分別對應著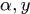 的矩陣形式。
的矩陣形式。
對應的響應

其中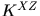 表示塊迴圈矩陣
表示塊迴圈矩陣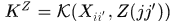 的生成矩陣。
的生成矩陣。
後面測試就類似於1D不推了
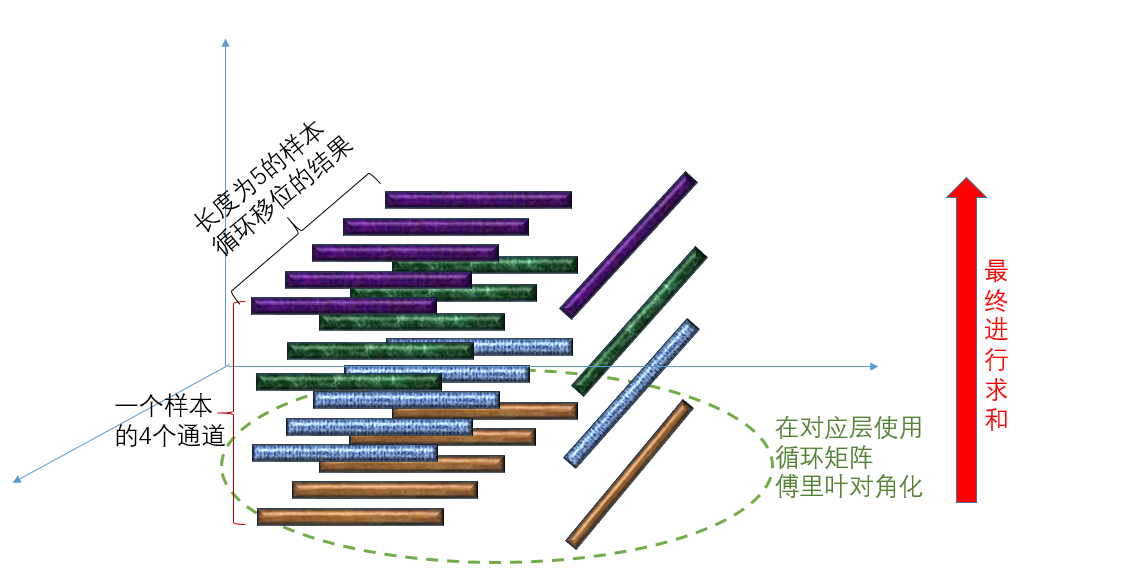
多通道問題
論文中在提取目標區域的特徵時可以是灰度特徵,但是使用Hog特徵能夠取得更好的效果,那麼Hog特徵該如何加入前面提到的模型呢?
Hog特徵是將影像劃分成較小的區域性塊,稱為cell,在cell裡提取梯度資訊,繪製梯度方向直方圖,然後為了減小光照影響,將幾個cell的方向直方圖串在一起進行block歸一化,最終將所有的cell直方圖串聯起來就是影像的特徵啦。
那麼,按照傳統的方式一張影像就提取出一個向量,但是這個向量怎麼用啊?我們又不能通過該向量的移位來獲得取樣樣本,因為,你想啊,把直方圖的一個bin迴圈移位有什麼意義啊?
所以論文中Hog特徵的提取是將sample區域劃分成若干的區域,然後再每個區域提取特徵,程式碼中是在每個區域提取了32維特徵,即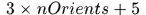 ,其中
,其中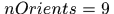 就是梯度方向劃分的bin個數,每個方向提取了3個特徵,2個是對方向bin敏感的,1個是不敏感的,另外4個特徵是關於表觀紋理的特徵還有一個是零,表示階段特徵,具體參見fhog。提取了31個特徵(最後一個0不考慮)之後,不是串聯起來,而是將每個cell的特徵並起來,那麼一幅影像得到的結果就是一個立體塊,假設劃分cell的結果是
就是梯度方向劃分的bin個數,每個方向提取了3個特徵,2個是對方向bin敏感的,1個是不敏感的,另外4個特徵是關於表觀紋理的特徵還有一個是零,表示階段特徵,具體參見fhog。提取了31個特徵(最後一個0不考慮)之後,不是串聯起來,而是將每個cell的特徵並起來,那麼一幅影像得到的結果就是一個立體塊,假設劃分cell的結果是 ,那麼fhog提取結果就是
,那麼fhog提取結果就是 ,我們成31這個方向為通道。那麼就可以通過cell的位移來獲得樣本,這樣對應的就是每一通道對應位置的移位,所有樣本的第i通道都是有生成影像的第i通道移位獲得的,
,我們成31這個方向為通道。那麼就可以通過cell的位移來獲得樣本,這樣對應的就是每一通道對應位置的移位,所有樣本的第i通道都是有生成影像的第i通道移位獲得的,
,所以分開在每一個通道上計算,就可以利用迴圈矩陣的性質了。
我們來看1D的情況,1D弄明白了,2D也就明白咯,因為我們上面說了怎麼推導2D的
樣本cell數為M,每個cell特徵維數為L,第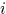 個樣本的第
個樣本的第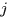 通道向量表示成
通道向量表示成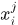 ,樣本的總特徵可以表示成
,樣本的總特徵可以表示成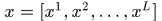 .
.
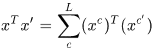
於是K矩陣的第一行有
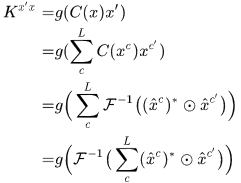
這裡用到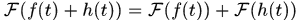
這是dot product kernel的情況,那徑向基核就很容易推了
總結
KCF相對於其他的tracking-by-detection方法速度得到了極大的提升,效果也相對較好,思想和實現十分簡單。

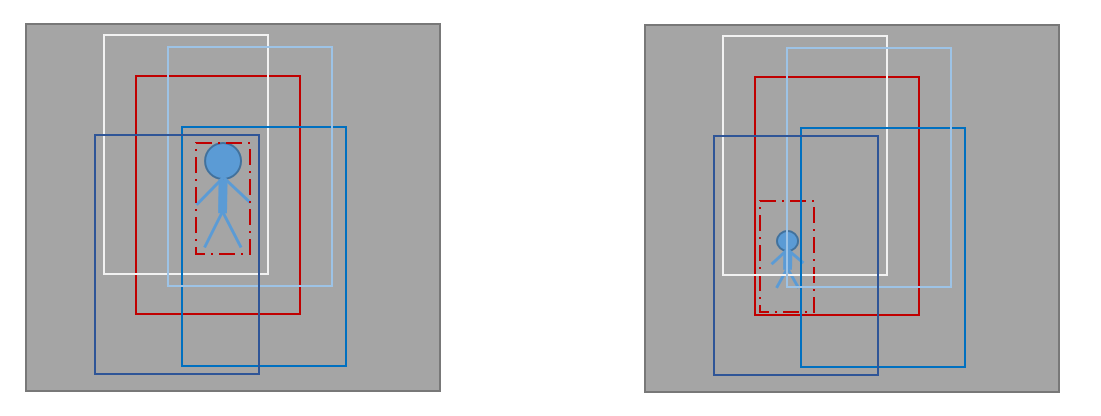
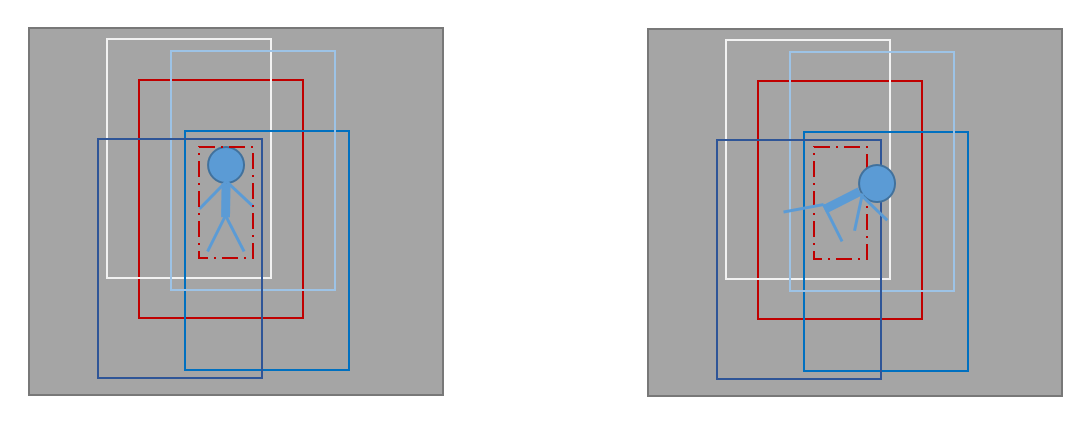
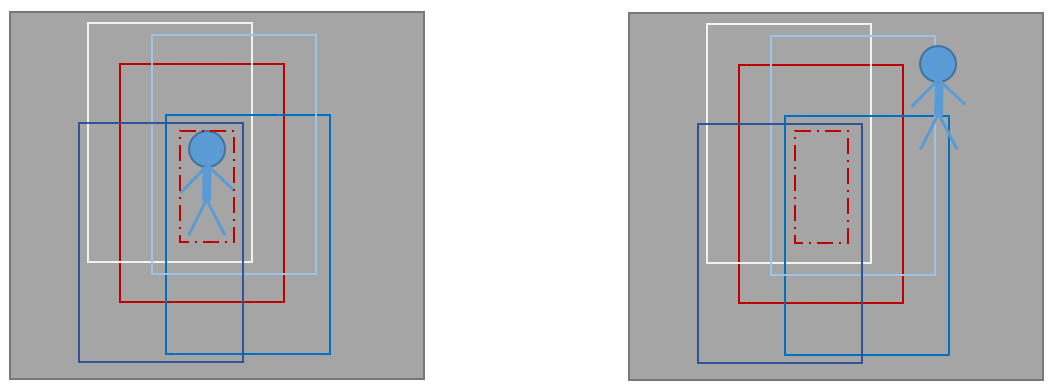
借上圖來總結下KCF的過程,左圖是剛開始我們使用紅色虛線框框定了目標,然後紅色實線框就是使用的padding了,其他的框就是將padding迴圈移位之後對齊目標得到的樣本,由這些樣本就可以訓練出一個分類器,當分類器設計好之後,來到了下一幀影像,也就是右圖,這時候我們首先在預測區域也就是紅色實線框區域取樣,然後對該取樣進行迴圈移位,對齊目標後就像圖中顯示的那個樣子 了,(這是為了理解,實際中不用對齊。。。),就是周圍那些框框啦,使用分類器對這些框框計算響應,顯然這時候白色框響應最大,因為他和之前一幀紅色框一樣,那我們通過白色框的相對移位就能推測目標的位移了。
然後繼續,再訓練再檢測。。。。
論文中還說到幾點
對特徵影像進行cosine window加權,這主要是為了減輕由於邊界移位導致影像不光滑。
padding的size是目標框的2.5倍,肯定要使用padding視窗,要不然移位一次目標就被分解重組合了。。。效果能好哪去。。
對於標籤使用了高斯加權
對
 前後幀結果進行了線性插值,為了讓他長記性,不至於模型劇烈變化。
前後幀結果進行了線性插值,為了讓他長記性,不至於模型劇烈變化。
但是其缺點也是很明顯的。
依賴迴圈矩陣,對於多尺度的目標跟蹤效果並不理想。當然可以通過設定多個size,在每個size上進行KCF運算,但這樣的話很難確定應預先設定多少size,什麼樣的size,而且對size的遍歷必將影響演算法的速度。KCF最大的優勢就是速度。
我在想能不能通過少量特徵點的匹配來調整視窗的size,當然這樣的話,速度也是個問題。
這種情況下還能保證最大響應就對應著目標中心所在的框嗎?如果不能偏差會不會越來越大?
初始化矩陣不能自適應改變,其實這個問題和上一個缺點類似,這裡強調的是非剛體運動,比如跳水運動員,剛開始選定區域肯定是個瘦長的矩形框,但當運動員開始屈體的時候顯然這個預選定框就很大誤差了。
3.難處理高速運動的目標
難處理低幀率中目標,這個和3類似,都是說相鄰幀間目標位移過大。
目標下一幀出現位置不在你的padding內,你怎麼也不可能移位找到。。。
5.雖然演算法中對模型係數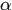 進行線性插值,但是對於目標一旦被遮擋若干幀之後,可能模型就再也回不去了。。。因為模型已經完全被遮擋物汙染掉了。
進行線性插值,但是對於目標一旦被遮擋若干幀之後,可能模型就再也回不去了。。。因為模型已經完全被遮擋物汙染掉了。
6.我覺的論文還有一個問題就是僅僅通過檢測到的框中心和目標實際中心的距離來度量效能,這是有問題的。
比如我現在有一個人垂直我的鏡頭逐漸遠去了,但他的中心一直在我鏡頭的中心處,那我就開始畫個框就是鏡頭的視角範圍,那這樣我檢測結果百分之百,可是有什麼用呢。。。。當然論文方法是在很多不同資料集上檢驗的效能還是很有說服力的。我的意思就是對於單個資料集不能僅憑這個指標定方法的好壞。