學過矩陣理論或者線性代數的肯定知道正交矩陣(orthogonal matrix)是一個非常好的矩陣,為什麼這麼說?原因有一下幾點:
- 正交矩陣每一列都是單位矩陣,並且兩兩正交。最簡單的正交矩陣就是單位陣。
- 正交矩陣的逆(inverse)等於正交矩陣的轉置(transpose)。同時可以推論出正交矩陣的行列式的值肯定為正負1的。
- 正交矩陣滿足很多矩陣性質,比如可以相似於對角矩陣等等。
以上可以看出正交矩陣是非常特殊的矩陣,而本文題目中的旋轉矩陣就是一種正交矩陣!它完美的詮釋了正交矩陣的所有特點。
先說一下什麼是旋轉矩陣?如圖1所示,我們假設最開始空間的座標系XA,YA,ZA就是笛卡爾座標系,這樣我們得到空間A的矩陣VA={XA,YA,ZA}T,其實也可以看做是單位陣E。進過旋轉後,空間A的三個座標系變成了圖1中紅色的三個座標系XB,YB,ZB,得到空間B的矩陣VB={XB,YB,ZB}T。我們將兩個空間聯絡起來可以得到VB=R•VA,這裡R就是我們所說的旋轉矩陣。
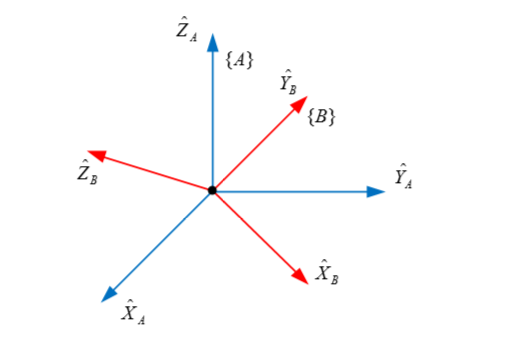
圖1
由於XA={1,0,0}T,YA={0,1,0}T,ZA={0,0,1}T,結合圖2可以看出,旋轉矩陣R就是由XB,YB,ZB 三個向量組成的。講到這裡,大家應該會發現旋轉矩陣R滿足第一個條件,因為單位向量無論怎麼旋轉長度肯定不會變而且向量之間的正交性質也不會變。那麼旋轉矩陣就是正交陣!不過這還不能說明問題,下面我更進一步利用數學公式進行證明。
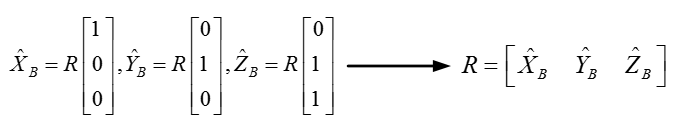
圖2
進一步討論之前,我們先說兩點數學知識。(1)點乘(dot product)的幾何意義:如圖3,我們從點乘的公式可以得到α•β相當與β的模乘上α在β上投影的模,所以當|β|=1時,α•β就是指α在β上投影的模。這一點在下面的內容中非常重要。(2)旋轉矩陣逆的幾何意思:這個比較抽象,不過也好理解。旋轉矩陣相當於把一個向量(空間)旋轉成新的向量(空間),那麼逆可以理解為由新的向量(空間)轉回原來的向量(空間)。
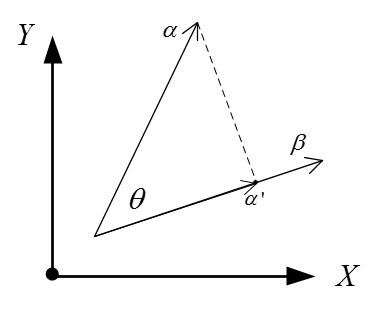
圖3
接下來就是重點了,我們結合圖4進行分析。上面已經說明了,旋轉矩陣R就是由XB,YB,ZB 三個向量組成的。我們來看看XB,YB,ZB究竟是什麼?由於圖中所有的向量均是單位向量,所以XB與XA點乘的結果可以看成XB在XA上的投影的模,也就是XB在空間A中x軸的分量!!圖中中間的位置列出了XB向量中的三個分量分別為XB在XA上的投影的模、XB在YA上的投影的模和XB在ZA上的投影的模。這從幾何角度很好理解。以此類推,可以得出的旋轉矩陣R的表達形式。我們根據圖4可以驚喜的發現,矩陣R的第一行就是XA在XB,YB,ZB上的投影的模,也就是XAT。
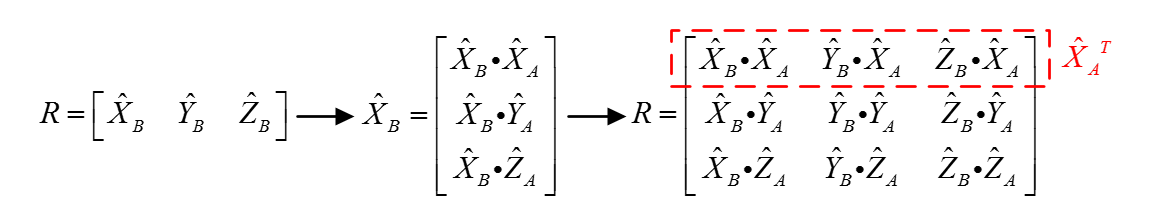
圖4
這個發現有什麼用呢?圖5做出解釋。根據上面公式可以推出A到B的旋轉矩陣等於B到A的旋轉矩陣的轉置。根據我們上一段所說的A到B的旋轉矩陣的逆就是等於B到A的旋轉矩陣,因此很容易推出R-1等於RT!這滿足正交矩陣的第二個條件,又一次證明了旋轉矩陣就是正交陣。在平時的工作中,我也測試過所有的旋轉矩陣的行列式的值都是為1的,所以旋轉矩陣滿足正交陣的一切性質,可以說是很完美的矩陣。
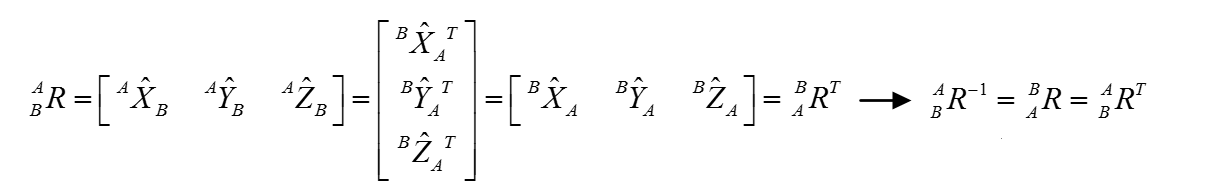
圖5
現在以三個尤拉角中的RotX為例(其餘兩個尤拉角以此類推),驗證一下以上說的結論。
首先結合圖5的公式,計算出RotX的旋轉矩陣Rrotx。
- 由於X軸是垂直於YoZ平面的,所以XA和YB,ZB的點乘結果為0,同時XB和YA,ZA的點乘結果也為0。
- 由於XA,XB都是單位向量,所以XA和XB的點乘結果為1。
- 由於繞x軸旋轉,所以我們觀察YB和ZB分別在YA和ZA上的投影情況,如圖6,我已經將座標標註了。
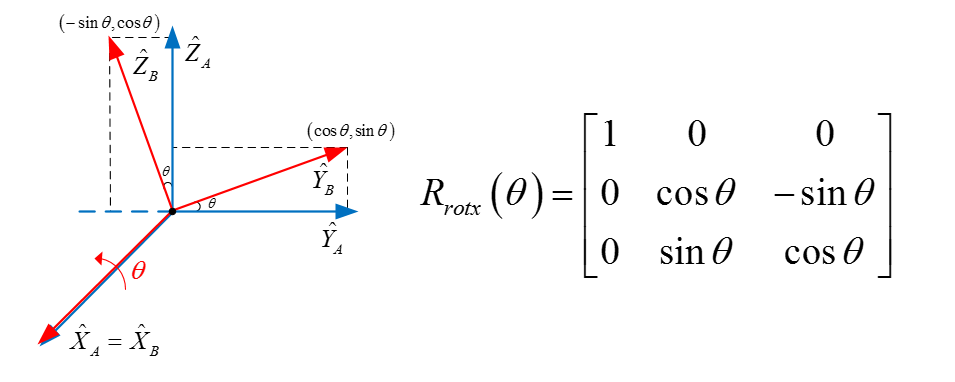
圖6
這樣就完成旋轉矩陣Rrotx,我們接下來驗證一下。
- 我們計算每一行每一列的模,都為1;並且任意兩個列向量或者任意兩個行向量都是正交的。所以滿足上文列出的第一個性質。
- 我們計算Rrotx的行列式,很簡單可以算出為1。這時我們計算一下該矩陣的逆和轉置,這裡我不寫出來了是相等的。所以滿足上文列出的第三個性質。
- 第三個性質要牽扯到更多的數學知識,在這裡就不驗證了。
總結一下:旋轉矩陣是一個完美的矩陣——正交矩陣。它的行列式為1,且每個列向量都是單位向量且相互正交,它的逆等於它的轉置。