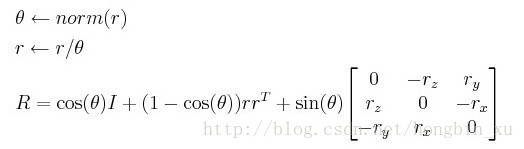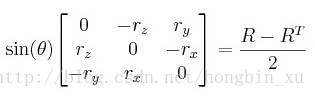三維重建學習(1):基礎知識:旋轉矩陣與旋轉向量
前言
由於攝像機標定中會使用到旋轉矩陣以及旋轉向量的知識,所以就整理了一下有關與這一部分基礎知識的筆記,並進行詳細的數學推導。
旋轉矩陣
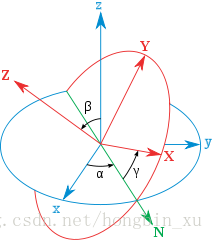
假設座標系分別繞著 x x x軸旋轉 ϕ \phi ϕ角,繞 y y y軸旋轉 θ \theta θ角,繞 z z z軸旋轉 ψ \psi ψ角,這裡旋轉的角度就是我們常說的pitch, roll, yaw。設任意某點在旋轉前的座標系中的座標是 ( x , y , z ) (x,y,z) (x,y,z),旋轉後的座標是 ( x ′ , y ′ , z ′ ) (x^{'}, y^{'}, z^{'}) (x′,y′,z′)。
我們可以很容易地推匯出這三種情況下的旋轉矩陣:
- 繞X軸旋轉φ角(PITCH):
R x = [ 1 0 0 0 cos ϕ − sin ϕ 0 sin ϕ cos ϕ ] R_x=\begin{bmatrix}1 & 0 & 0 \\ 0 & \cos{\phi} & -\sin{\phi} \\ 0 & \sin{\phi} & \cos{\phi} \end{bmatrix} Rx=⎣⎡1000cosϕsinϕ0−sinϕcosϕ⎦⎤
- 繞Y軸旋轉θ角(ROLL):
R y = [ cos θ 0 sin θ 0 1 0 − sin θ 0 cos θ ] R_y=\begin{bmatrix} \cos{\theta} & 0 & \sin{\theta} \\ 0 & 1 & 0 \\ - \sin{\theta} & 0 & \cos{\theta} \end{bmatrix} Ry=⎣⎡cosθ0−sinθ010sinθ0cosθ⎦⎤
- 繞Z軸旋轉ψ角(YAW):
R z = [ cos ψ − sin ψ 0 sin ψ cos ψ 0 0 0 1 ] R_z=\begin{bmatrix} \cos{\psi} & -\sin{\psi} & 0 \\ \sin{\psi} & \cos{\psi} & 0 \\ 0 & 0 & 1 \end{bmatrix} Rz=⎣⎡cosψsinψ0−sinψcosψ0001⎦⎤
詳細步驟我就不列出來了,我以前的部落格中有詳細的推導步驟,雖然使用場景不同,但是概念都是一樣的。(四旋翼姿態解算——基礎理論及推導)
如果已經上面的三個角度 ϕ \phi ϕ、 θ \theta θ、 ψ \psi ψ,,我們可以通過將每一步的旋轉矩陣相乘得到整個旋轉矩陣。
R = R x ∗ R y ∗ R z R=R_x * R_y *R_z R=Rx∗Ry∗Rz
旋轉向量
相機標定中表示旋轉的方式,除了使用前面介紹的旋轉矩陣之外,還可以使用旋轉向量來表示。
我在網上搜尋相關資料時,發現大多數都是直接給出了Rodrigue旋轉向量的公式,而沒有推導過程。如果只是拿來用,那肯定是沒問題的,但是不把它的公式推導一遍,心裡總是有點不踏實。(好吧,我知道我有點廢話)下面我會給出我自己的證明步驟,在最後會給出公式。
補充概念:向量的拉格朗日公式
對於任意向量 a ⃗ ( a 1 , a 2 , a 3 ) \vec{a}(a_1,a_2,a_3) a(a1,a2,a3), b ⃗ ( b 1 , b 2 , b 3 ) \vec{b}(b_1,b_2,b_3) b(b1,b2,b3), c ⃗ ( c 1 , c 2 , c 3 ) \vec{c}(c_1,c_2,c_3) c(c1,c2,c3),有如下公式成立:
a ⃗ × ( b ⃗ × c ⃗ ) = ( a ⃗ ⋅ c ⃗ ) b ⃗ − ( a ⃗ ⋅ b ⃗ ) c ⃗ \vec{a} \times (\vec{b} \times \vec{c}) = (\vec{a} \cdot \vec{c})\vec{b} - (\vec{a} \cdot \vec{b}) \vec{c} a×(b×c)=(a⋅c)b−(a⋅b)c
證明如下:
設 d ⃗ = b ⃗ × c ⃗ \vec{d} = \vec{b} \times \vec{c} d=b×c,且可表示為 d ⃗ ( d 1 , d 2 , d 3 ) \vec{d}(d_1,d_2,d_3) d(d1,d2,d3)。
則有: d ⃗ = b ⃗ × c ⃗ = [ i ⃗ j ⃗ k ⃗ b 1 b 2 b 3 c 1 c 2 c 3 ] = i ⃗ ( b 2 c 3 − b 3 c 2 ) − j ⃗ ( b 1 c 3 − b 3 c 1 ) + k ⃗ ( b 1 c 2 − b 2 c 1 ) \vec{d} = \vec{b} \times \vec{c}=\begin{bmatrix} \vec{i} & \vec{j} & \vec{k} \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{bmatrix}\\=\vec{i}(b_2c_3-b_3c_2)-\vec{j}(b_1c_3-b_3c_1)+\vec{k}(b_1c_2-b_2c_1) d=b×c=⎣⎡ib1c1jb2c2kb3c3⎦⎤=i(b2c3−b3c2)−j(b1c3−b3c1)+k(b1c2−b2c1)
對應地就有: d 1 = b 2 c 3 − b 3 c 2 d_1=b_2c_3-b_3c_2 d1=b2c3−b3c2、 d 2 = b 3 c 1 − b 1 c 3 d_2=b_3c_1-b_1c_3 d2=b3c1−b1c3、 d 3 = b 1 c 2 − b 2 c 1 d_3=b_1c_2-b_2c_1 d3=b1c2−b2c1。
再設 e ⃗ = a ⃗ × d ⃗ = a ⃗ × ( b ⃗ × c ⃗ ) \vec{e} = \vec{a} \times \vec{d} = \vec{a} \times (\vec{b} \times \vec{c}) e=a×d=a×(b×c),且可表示為 e ⃗ ( e 1 , e 2 , e 3 ) \vec{e}(e_1,e_2,e_3) e(e1,e2,e3)。
那麼: e ⃗ = a ⃗ × d ⃗ = [ i ⃗ j ⃗ k ⃗ a 1 a 2 a 3 d 1 d 2 d 3 ] = i ⃗ ( a 2 d 3 − a 3 d 2 ) − j ⃗ ( a 1 d 3 − a 3 d 1 ) + k ⃗ ( a 1 d 2 − a 2 d 1 ) \vec{e} = \vec{a} \times \vec{d}=\begin{bmatrix} \vec{i} & \vec{j} & \vec{k} \\ a_1 & a_2 & a_3 \\ d_1 & d_2 & d_3 \end{bmatrix}\\=\vec{i}(a_2d_3-a_3d_2)-\vec{j}(a_1d_3-a_3d_1)+\vec{k}(a_1d_2-a_2d_1) e=a×d=⎣⎡ia1d1ja2d2ka3d3⎦⎤=i(a2d3−a3d2)−j(a1d3−a3d1)+k(a1d2−a2d1)
對應地得到得到: e 1 = a 2 d 3 − a 3 d 2 e_1=a_2d_3-a_3d_2 e1=a2d3−a3d2、 e 2 = a 1 d 3 − a 3 d 1 e_2=a_1d_3-a_3d_1 e2=a1d3−a3d1、 e 3 = a 1 d 2 − a 2 d 1 e_3=a_1d_2-a_2d_1 e3=a1d2−a2d1
對於 e 1 e_1 e1,代入前面推匯出來的 d 2 d_2 d2、 d 3 d_3 d3:
e 1 = a 2 d 3 − a 3 d 2 = a 2 ( b 1 c 2 − b 2 c 1 ) − a 3 ( b 3 c 1 − b 1 c 3 ) = b 1 ( a 2 c 2 + a 3 c 3 ) − c 1 ( a 3 b 3 + a 2 b 2 ) = b 1 ( a ⃗ ⋅ c ⃗ − a 1 c 1 ) − c 1 ( a ⃗ ⋅ b ⃗ − a 1 b 1 ) = b 1 ( a ⃗ ⋅ c ⃗ ) − c 1 ( a ⃗ ⋅ b ⃗ ) e_1=a_2d_3-a_3d_2=a_2(b_1c_2-b_2c_1)-a_3(b_3c_1-b_1c_3) \\ =b_1 (a_2c_2 + a_3c_3) - c_1 (a_3b_3 + a_2b_2) \\ = b_1 (\vec{a} \cdot \vec{c} - a_1c_1) - c_1 (\vec{a} \cdot \vec{b} - a_1b_1) \\ = b_1 (\vec{a} \cdot \vec{c}) - c_1 (\vec{a} \cdot \vec{b}) e1=a2d3−a3d2=a2(b1c2−b2c1)−a3(b3c1−b1c3)=b1(a2c2+a3c3)−c1(a3b3+a2b2)=b1(a⋅c−a1c1)−c1(a⋅b−a1b1)=b1(a⋅c)−c1(a⋅b)
同理可得:
e 2 = b 2 ( a ⃗ ⋅ c ⃗ ) − c 2 ( a ⃗ ⋅ b ⃗ ) e_2 = b_2 (\vec{a} \cdot \vec{c}) - c_2 (\vec{a} \cdot \vec{b}) e2=b2(a⋅c)−c2(a⋅b)
e 3 = b 3 ( a ⃗ ⋅ c ⃗ ) − c 3 ( a ⃗ ⋅ b ⃗ ) e_3 = b_3 (\vec{a} \cdot \vec{c}) - c_3 (\vec{a} \cdot \vec{b}) e3=b3(a⋅c)−c3(a⋅b)
把這三個式子合併,表示成向量形式:
e ⃗ = b ⃗ ( a ⃗ ⋅ c ⃗ ) − c ⃗ ( a ⃗ ⋅ b ⃗ ) \vec{e} = \vec{b} (\vec{a} \cdot \vec{c}) - \vec{c} (\vec{a} \cdot \vec{b}) e=b(a⋅c)−c(a⋅b)
證明完畢,後面我們還會用到這個公式。
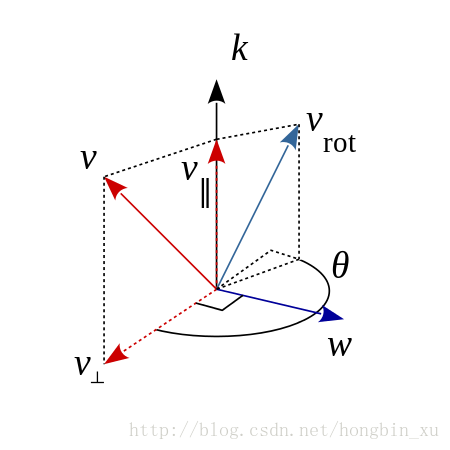
上圖摘自維基百科。假設我們在任意空間中有任意一個向量 v ⃗ \vec{v} v, k ⃗ \vec{k} k是某個單位向量。現在,我們將向量 v ⃗ \vec{v} v以單位向量 k ⃗ \vec{k} k為軸,旋轉任意角度 θ \theta θ,得到旋轉後的向量 v r o t ⃗ \vec{v_{rot}} vrot如圖中所示。在圖中,我們將 v ⃗ \vec{v} v關於 k ⃗ \vec{k} k做正交分解(高中物理),會得到兩個新的向量: v ⊥ ⃗ \vec{v_{\bot}} v⊥和 v ∥ ⃗ \vec{v_{\parallel}} v∥。
很明顯: v ⊥ ⃗ \vec{v_{\bot}} v⊥與 k ⃗ \vec{k} k相互垂直, v ∥ ⃗ \vec{v_{\parallel}} v∥與 k ⃗ \vec{k} k共線(平行),且還有 v ⃗ = v ⊥ ⃗ + v ∥ ⃗ \vec{v}=\vec{v_{\bot}}+\vec{v_{\parallel}} v=v⊥+v∥。
因為 v ∥ ⃗ \vec{v_{\parallel}} v∥與 k ⃗ \vec{k} k共線,且 k ⃗ \vec{k} k是一個單位向量,所以:
v ∥ ⃗ = ∥ v ∥ ⃗ ∥ ⋅ k ⃗ = v ⃗ ⋅ k ⃗ ∥ k ⃗ ∥ ⋅ k ⃗ = ( v ⃗ ⋅ k ⃗ ) ⋅ k ⃗ \vec{v_{\parallel}}=\|\vec{v_{\parallel}}\| \cdot \vec{k}= \frac{\vec{v} \cdot \vec{k}}{\| \vec{k} \|} \cdot \vec{k} = (\vec{v} \cdot \vec{k}) \cdot \vec{k} v∥=∥v∥∥⋅k=∥k∥v⋅k⋅k=(v⋅k)⋅k
接下來求 v ⊥ ⃗ \vec{v_{\bot}} v⊥,由我們前面推導的向量的拉格朗日定理: a ⃗ × ( b ⃗ × c ⃗ ) = ( a ⃗ ⋅ c ⃗ ) b ⃗ − ( a ⃗ ⋅ b ⃗ ) c ⃗ \vec{a} \times (\vec{b} \times \vec{c}) = (\vec{a} \cdot \vec{c})\vec{b} - (\vec{a} \cdot \vec{b}) \vec{c} a×(b×c)=(a⋅c)b−(a⋅b)c,有:
k ⃗ × ( k ⃗ × v ⃗ ) = ( k ⃗ ⋅ v ⃗ ) ⋅ k ⃗ − ( k ⃗ ⋅ k ⃗ ) ⋅ v ⃗ = ( k ⃗ ⋅ v ⃗ ) ⋅ k ⃗ − v ⃗ \vec{k} \times (\vec{k} \times \vec{v}) = (\vec{k} \cdot \vec{v}) \cdot \vec{k} - (\vec{k} \cdot \vec{k}) \cdot \vec{v}=(\vec{k} \cdot \vec{v}) \cdot \vec{k} - \vec{v} k×(k×v)=(k⋅v)⋅k−(k⋅k)⋅v=(k⋅v)⋅k−v
然後,我們就可以推出:
v ⊥ ⃗ = v ⃗ − v ∥ ⃗ = − k ⃗ × ( k ⃗ × v ⃗ ) \vec{v_{\bot}}=\vec{v} - \vec{v_{\parallel}} = -\vec{k} \times (\vec{k} \times \vec{v}) v⊥=v−v∥=−k×(k×v)
我們可以根據前面給出的示意圖來直觀地理解這些式子: k ⃗ × v ⃗ \vec{k} \times \vec{v} k×v可以看作是 v ⊥ ⃗ \vec{v_{\bot}} v⊥繞著 k ⃗ \vec{k} k逆時針旋轉90度得到的,即圖中的 w ⃗ = k ⃗ × v ⃗ \vec{w}=\vec{k} \times \vec{v} w=k×v;對於 k ⃗ × ( k ⃗ × v ⃗ ) = k ⃗ × w ⃗ \vec{k} \times (\vec{k} \times \vec{v})=\vec{k} \times\vec{w} k×(k×v)=k×w,在圖中觀察發現,這個式子的結果其實就是 v ⊥ ⃗ \vec{v_{\bot}} v⊥繞著 k ⃗ \vec{k} k逆時針旋轉180度得到的結果,共線且夾角為180度,正好對應推匯出的結果: v ⊥ ⃗ = − k ⃗ × ( k ⃗ × v ⃗ ) \vec{v_{\bot}} = -\vec{k} \times (\vec{k} \times \vec{v}) v⊥=−k×(k×v)。
還是根據這幅圖來看,旋轉過程中 v ∥ ⃗ \vec{v_{\parallel}} v∥的大小始終不變,因為它是 v ⃗ \vec{v} v在 k ⃗ \vec{k} k方向上的投影,就在旋轉軸上,自然不會變。所以有: v r o t , ∥ ⃗ = v ∥ ⃗ \vec{v_{rot, \parallel}} = \vec{v_{\parallel}} vrot,∥=v∥。
接下來看 v r o t , ⊥ ⃗ \vec{v_{rot, \bot}} vrot,⊥的變化:
首先,可以肯定的是旋轉過程中向量的模長不變,只會改變方向,所以: ∥ v r o t , ⊥ ⃗ ∥ = ∥ v ⊥ ⃗ ∥ \| \vec{v_{rot, \bot}} \| = \| \vec{v_{\bot}} \| ∥vrot,⊥∥=∥v⊥∥。
我們可以由 v ⊥ ⃗ \vec{v_{\bot}} v⊥和 k ⃗ \vec{k} k方向的投影,組合得到 v r o t , ⊥ ⃗ \vec{v_{rot, \bot}} vrot,⊥:
v r o t , ⊥ ⃗ = v ⊥ ⃗ cos θ + ∥ v ⊥ ⃗ ∥ sin θ w ⃗ ∥ w ⃗ ∥ \vec{v_{rot, \bot}}=\vec{v_{\bot}}\cos\theta + \| \vec{v_{\bot}} \| \sin\theta \frac{\vec{w}}{\|\vec{w}\|} vrot,⊥=v⊥cosθ+∥v⊥∥sinθ∥w∥w
前面有: w ⃗ = k ⃗ × v ⃗ \vec{w}=\vec{k} \times \vec{v} w=k×v可以看作是 v ⊥ ⃗ \vec{v_{\bot}} v⊥繞著 k ⃗ \vec{k} k逆時針旋轉90度得到的。那麼有: ∥ v ⊥ ⃗ ∥ = ∥ w ⃗ ∥ \| \vec{v_{\bot}} \| = \|\vec{w}\| ∥v⊥∥=∥w∥。
上式可以化簡為:
v r o t , ⊥ ⃗ = v ⊥ ⃗ cos θ + sin θ w ⃗ = v ⊥ ⃗ cos θ + sin θ ( k ⃗ × v ⃗ ) \vec{v_{rot, \bot}} = \vec{v_{\bot}}\cos\theta + \sin\theta \vec{w}= \vec{v_{\bot}}\cos\theta + \sin\theta (\vec{k} \times \vec{v}) vrot,⊥=v⊥cosθ+sinθw=v⊥cosθ+sinθ(k×v)
將 v r o t , ⊥ ⃗ \vec{v_{rot, \bot}} vrot,⊥和 v r o t , ∥ ⃗ \vec{v_{rot, \parallel}} vrot,∥相加,即可得到 v r o t ⃗ \vec{v_{rot}} vrot:
v r o t ⃗ = v r o t , ⊥ ⃗ + v r o t , ∥ ⃗ = v ∥ ⃗ + v ⊥ ⃗ cos θ + sin θ ( k ⃗ × v ⃗ ) = v ∥ ⃗ + ( v ⃗ − v ∥ ⃗ ) cos θ + sin θ ( k ⃗ × v ⃗ ) = v ⃗ cos θ + ( 1 − cos θ ) v ∥ ⃗ + sin θ ( k ⃗ × v ⃗ ) \begin{aligned} \vec{v_{rot}} &= \vec{v_{rot, \bot}} + \vec{v_{rot, \parallel}} \\ &= \vec{v_{\parallel}} + \vec{v_{\bot}}\cos\theta + \sin\theta (\vec{k} \times \vec{v}) \\ &= \vec{v_{\parallel}} + (\vec{v} - \vec{v_{\parallel}}) \cos\theta +\sin\theta (\vec{k} \times \vec{v}) \\ &= \vec{v}\cos\theta + (1-\cos\theta) \vec{v_{\parallel}} + \sin\theta (\vec{k} \times \vec{v}) \end{aligned} vrot=vrot,⊥+vrot,∥=v∥+v⊥cosθ+sinθ(k×v)=v∥+(v−v∥)cosθ+sinθ(k×v)=vcosθ+(1−cosθ)v∥+sinθ(k×v)
前面推出來了: v ∥ ⃗ = ∥ v ∥ ⃗ ∥ ⋅ k ⃗ = v ⃗ ⋅ k ⃗ ∥ k ⃗ ∥ ⋅ k ⃗ = ( v ⃗ ⋅ k ⃗ ) ⋅ k ⃗ \vec{v_{\parallel}}=\|\vec{v_{\parallel}}\| \cdot \vec{k}= \frac{\vec{v} \cdot \vec{k}}{\| \vec{k} \|} \cdot \vec{k} = (\vec{v} \cdot \vec{k}) \cdot \vec{k} v∥=∥v∥∥⋅k=∥k∥v⋅k⋅k=(v⋅k)⋅k,直接把那個結論代入這裡。
v r o t ⃗ = v ⃗ cos θ + ( 1 − cos θ ) ( v ⃗ ⋅ k ⃗ ) ⋅ k ⃗ + sin θ ( k ⃗ × v ⃗ ) \begin{aligned} \vec{v_{rot}} &= \vec{v}\cos\theta + (1-\cos\theta) (\vec{v} \cdot \vec{k}) \cdot \vec{k} + \sin\theta (\vec{k} \times \vec{v}) \end{aligned} vrot=vcosθ+(1−cosθ)(v⋅k)⋅k+sinθ(k×v)
現在我們已經推匯出了旋轉向量公示了,我們可以套用這個公式來表示任意旋轉。
接下來要進一步整理成矩陣形式:
對於 k ⃗ × v ⃗ \vec{k} \times \vec{v} k×v,用矩陣形式來表示:(無非就是向量叉乘,拆成三個軸上的分量來表示)
[ ( k ⃗ × v ⃗ ) x ( k ⃗ × v ⃗ ) y ( k ⃗ × v ⃗ ) z ] = [ k y v z − k z v y k z v x − k x v z k x v y − k y v x ] = [ 0 − k z k y k z 0 − k x − k y k x 0 ] ⋅ [ v x v y v z ] \begin{bmatrix} (\vec{k} \times \vec{v})_x \\ (\vec{k} \times \vec{v})_y \\ (\vec{k} \times \vec{v})_z \end{bmatrix} = \begin{bmatrix}k_yv_z-k_zv_y \\ k_zv_x-k_xv_z \\ k_xv_y - k_yv_x \end{bmatrix} = \begin{bmatrix} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x &0 \end{bmatrix} \cdot \begin{bmatrix} v_x \\ v_y \\ v_z\end{bmatrix} ⎣⎢⎡(k×v)x(k×v)y(k×v)z⎦⎥⎤=⎣⎡kyvz−kzvykzvx−kxvzkxvy−kyvx⎦⎤=⎣⎡0kz−ky−kz0kxky−kx0⎦⎤⋅⎣⎡vxvyvz⎦⎤
使用一個大寫的 K K K來表示:
K = [ 0 − k z k y k z 0 − k x − k y k x 0 ] K=\begin{bmatrix} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x &0 \end{bmatrix} K=⎣⎡0kz−ky−kz0kxky−kx0⎦⎤
那麼有: K v ⃗ = k ⃗ × v ⃗ K\vec{v}=\vec{k} \times \vec{v} Kv=k×v
還有: K ( K v ⃗ ) = K 2 v ⃗ = K ( k ⃗ × v ⃗ ) = k ⃗ × ( K v ⃗ ) = k ⃗ × ( k ⃗ × v ⃗ ) K(K\vec{v})=K^2\vec{v}=K(\vec{k} \times \vec{v}) = \vec{k} \times (K\vec{v}) = \vec{k} \times (\vec{k} \times \vec{v}) K(Kv)=K2v=K(k×v)=k×(Kv)=k×(k×v)
公式可以進一步化簡為:
v r o t ⃗ = v ⃗ cos θ + ( 1 − cos θ ) ( v ⃗ ⋅ k ⃗ ) ⋅ k ⃗ + sin θ ( k ⃗ × v ⃗ ) = v ⃗ cos θ + ( 1 − cos θ ) ( v ⃗ + k ⃗ × ( k ⃗ × v ⃗ ) ) + sin θ ( k ⃗ × v ⃗ ) = v ⃗ + ( 1 − cos θ ) K 2 v ⃗ + s i n θ K v ⃗ \begin{aligned} \vec{v_{rot}} &= \vec{v}\cos\theta + (1-\cos\theta) (\vec{v} \cdot \vec{k}) \cdot \vec{k} + \sin\theta (\vec{k} \times \vec{v}) \\ &= \vec{v}\cos\theta + (1-\cos\theta) (\vec{v} + \vec{k} \times (\vec{k} \times \vec{v})) + \sin\theta (\vec{k} \times \vec{v}) \\ &= \vec{v} + (1-\cos\theta)K^2\vec{v} + sin\theta K \vec{v} \end{aligned} vrot=vcosθ+(1−cosθ)(v⋅k)⋅k+sinθ(k×v)=vcosθ+(1−cosθ)(v+k×(k×v))+sinθ(k×v)=v+(1−cosθ)K2v+sinθKv
給出旋轉矩陣 R R R有: v r o t ⃗ = R v ⃗ \vec{v_{rot}} = R \vec{v} vrot=Rv
那麼消去 v ⃗ \vec{v} v:$R = I + (1-\cos\theta)K^2 + sin\theta K $
Rodrigue旋轉向量公式
已知單位向量 k ⃗ = ( k x , k y , k z ) \vec{k}=(k_x,k_y,k_z) k=(kx,ky,kz),向量 v ⃗ \vec{v} v繞著它旋轉 θ \theta θ角。旋轉後的向量 v r o t ⃗ \vec{v_{rot}} vrot可以通過如下公式求得:
v r o t ⃗ = v ⃗ cos θ + ( 1 − cos θ ) ( v ⃗ ⋅ k ⃗ ) ⋅ k ⃗ + sin θ ( k ⃗ × v ⃗ ) \begin{aligned} \vec{v_{rot}} &= \vec{v}\cos\theta + (1-\cos\theta) (\vec{v} \cdot \vec{k}) \cdot \vec{k} + \sin\theta (\vec{k} \times \vec{v}) \end{aligned} vrot=vcosθ+(1−cosθ)(v⋅k)⋅k+sinθ(k×v)
我們可以把 v ⃗ \vec{v} v提取出來,就得到了:
v r o t ⃗ = R v ⃗ = ( I ⋅ cos θ + ( 1 − cos θ ) k ⃗ ⋅ k ⃗ + sin θ K ) v ⃗ \begin{aligned} \vec{v_{rot}} &= R \vec{v} \\ &= (I \cdot \cos\theta + (1-\cos\theta) \vec{k} \cdot \vec{k} + \sin\theta K)\vec{v} \end{aligned} vrot=Rv=(I⋅cosθ+(1−cosθ)k⋅k+sinθK)v
其中:
K = [ 0 − k z k y k z 0 − k x − k y k x 0 ] K=\begin{bmatrix} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x &0 \end{bmatrix} K=⎣⎡0kz−ky−kz0kxky−kx0⎦⎤
根據上面這個式子,我們可以給出Rodrigue旋轉公式:
對於旋轉向量
r
⃗
=
(
r
x
,
r
y
,
r
z
)
\vec{r} = (r_x, r_y, r_z)
r=(rx,ry,rz):
θ \theta θ為向量 r ⃗ \vec{r} r的模長,而且要保證向量 r ⃗ \vec{r} r是一個單位向量。
反變換也可以很容易求出:
注:在opencv中有相關的實現(Rodrigues2函式)
當然還有一種寫法:
v r o t ⃗ = R v ⃗ = I ⋅ v ⃗ + ( 1 − cos θ ) K 2 ⋅ v ⃗ + s i n θ K ⋅ v ⃗ \vec{v_{rot}} = R\vec{v} = I \cdot \vec{v} + (1-\cos\theta)K^2 \cdot \vec{v} + sin\theta K \cdot \vec{v} vrot=Rv=I⋅v+(1−cosθ)K2⋅v+sinθK⋅v
對應的旋轉矩陣:(我們可以用這個公式來求旋轉矩陣)
R = I + ( 1 − cos θ ) K 2 + s i n θ K R = I + (1-\cos\theta)K^2 + sin\theta K R=I+(1−cosθ)K2+sinθK
其中:
K = [ 0 − k z k y k z 0 − k x − k y k x 0 ] K=\begin{bmatrix} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x &0 \end{bmatrix} K=⎣⎡0kz−ky−kz0kxky−kx0⎦⎤
參考連結:
相關文章
- 三維旋轉:旋轉矩陣,尤拉角,四元數矩陣
- 三維旋轉矩陣推導矩陣
- 利用三維旋轉矩陣在空間中旋轉平面矩陣
- 剛體在三維空間的旋轉(關於旋轉矩陣、DCM、旋轉向量、四元數、尤拉角)矩陣
- 圖形學 旋轉與投影矩陣—1矩陣
- 三維座標系旋轉——旋轉矩陣到旋轉角之間的換算矩陣
- 三維座標系的旋轉矩陣矩陣
- 旋轉矩陣矩陣
- 矩陣旋轉矩陣
- 旋轉變換(一)旋轉矩陣矩陣
- 二維旋轉矩陣推導矩陣
- lisp 習題 矩陣旋轉Lisp矩陣
- 三維空間 旋轉矩陣 四元數 尤拉角 相互轉換 組合旋轉矩陣
- 圖形學 旋轉與投影矩陣—2矩陣
- 圖形學 旋轉與投影矩陣-3矩陣
- 三維旋轉矩陣 左乘和右乘分析矩陣
- 旋轉矩陣推導矩陣
- 三維空間座標系變換-旋轉矩陣矩陣
- 旋轉矩陣與尤拉角的相互轉換矩陣
- 三維圖形繞任意軸旋轉矩陣求解步驟矩陣
- 三維空間中物體兩次旋轉之間的連續旋轉矩陣計算矩陣
- 原地旋轉矩陣(不申請新的記憶體空間旋轉矩陣)矩陣記憶體
- 三維空間變換中旋轉矩陣左乘與右乘的區別矩陣
- 空間旋轉矩陣怎麼表示矩陣
- 正方形矩陣旋轉90度矩陣
- THREE 矩陣優先原則和平移旋轉矩陣矩陣
- 第四個OpenGL程式,vector 向量 (矩陣變換之 旋轉,縮放)矩陣
- 3D旋轉矩陣的推導3D矩陣
- 旋轉矩陣(Rotate Matrix)的性質分析矩陣
- 三維旋轉矩陣的推導過程(以右手座標系為例)矩陣
- 遊戲基礎知識——迴歸、凱旋遊戲
- 三相電合成旋轉向量-動態圖
- 矩陣旋轉-Eigen應用(QTCreator編輯器)矩陣QT
- 矩陣變換:沿任意軸旋轉及其推導矩陣
- 旋轉的數學表達:尤拉角、軸向角、四元數與矩陣矩陣
- 旋轉向量合成,兩個圓圈
- 註冊 旋轉矩陣 1.99 (1012字)矩陣
- 社交網路分析的 R 基礎:(三)向量、矩陣與列表矩陣