原文見我的部落格主站,歡迎大家過去評論。
如何描述三維空間中剛體的旋轉,是個有趣的問題。具體地說,就是剛體上的任意一個點P(x, y, z)圍繞過原點的軸(i, j, k)旋轉θ,求旋轉後的點P\'(x\', y\', z\')。
旋轉矩陣
旋轉矩陣乘以點P的齊次座標,得到旋轉後的點P',因此旋轉矩陣可以描述旋轉,
$$\begin{bmatrix}x'\\ y'\\ z'\\ 1\end{bmatrix}=R\cdot \begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}$$
繞x,y,或z軸旋轉θ的矩陣為:
$$R_{x}(\theta)=\begin{bmatrix}1 & 0 & 0\\ 0 & \cos\theta & -\sin\theta\\ 0 & \sin\theta & \cos\theta\end{bmatrix}$$
$$R_{y}(\theta)=\begin{bmatrix}\cos\theta & 0 & -\sin\theta\\ 0 & 1 & 0\\ \sin\theta & 0 & \cos\theta\end{bmatrix}$$
$$R_{z}(\theta)=\begin{bmatrix}\cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1\end{bmatrix}$$
所以,繞任意軸旋轉的矩陣為
$$R_{x}(-p)\cdot R_{y}(-q)\cdot R_{z}(\theta)\cdot R_{y}(q)\cdot R_{x}(p)$$
這表示:
1. 繞x軸旋轉角度p使指定的旋轉軸在xz平面上
2. 繞y軸旋轉角度q使指定的旋轉軸與z軸重合
3. 繞z軸旋轉角度θ
4. 繞y軸旋轉角度-q
5. 繞x軸旋轉角度-p
其中,p和q的值需要用i,j,k計算出來。
尤拉角
尤拉角也可以描述三維剛體旋轉,它將剛體繞過原點的軸(i,j,k)旋轉θ,分解成三步(藍色是起始座標系,而紅色的是旋轉之後的座標系。)。
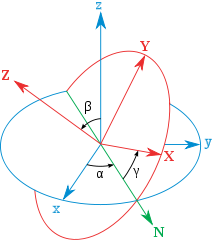
1. 繞z軸旋轉α,使x軸與N軸重合,N軸是旋轉前後兩個座標系x-y平面的交線
2. 繞x軸(也就是N軸)旋轉β,使z軸與旋轉後的z軸重合
3. 繞z軸旋轉γ,使座標系與旋轉後的完全重合
按照旋轉軸的順序,該組尤拉角被稱為是“zxz順規”的。對於順規的次序,學術界沒有明確的約定。
尤拉角的旋轉矩陣為:
$$R_{z}(α)\cdot R_{x}(β)\cdot R_{z}(γ)$$
在旋轉矩陣一節中,最先進行的旋轉其矩陣在最右側,說明該矩陣最先與點的齊次座標相乘,旋轉矩陣按照旋轉的次序從右向左排列。而在尤拉角中,最先進行的旋轉其旋轉矩陣在最左邊。這是因為,**對於前者(旋轉矩陣),我們始終是以絕對參考系為參照來的,對於後者(尤拉角),我們每一次旋轉的刻畫都是基於剛體的座標系。**比如,在尤拉角中的第2步,繞x軸旋轉β,這裡的x軸實際上是N軸了(而不是藍色的x軸)。
為什麼旋轉參考系的不同會導致旋轉矩陣次序的差異呢?細想一下便知,旋轉矩陣左乘疊加用以描述三維變換效果的疊加,這本身就是基於絕對座標系的,所以旋轉矩陣一節沒有疑問;而對於尤拉角一節的這種旋轉方式,這樣考慮:
1. 如果有一個“影子座標系3”與原座標系重合,然後首先進行了第3步(繞z軸旋轉γ);
2. 然後有一個“影子座標系2”也與原座標系重合,然後與“影子座標系3”一起(視作同一個剛體)進行了第二步;
3. 最後一個“影子座標系1”,與前兩個座標系一起進行了第一步。
此時,考察“影子座標系”1和2,他們就分別落在了尤拉角旋轉的兩個“快照”上,而“影子座標系3”就落在旋轉後的位置上(紅色的)。而在上述過程中,“影子座標系3”就是相對於絕對座標系依次進行了第三步,第二步,和第一步。所以尤拉角的旋轉矩陣寫成那樣,也是行得通的。
這個想法,我猜在很多第一人稱遊戲中,已經得到了廣泛應用了。這樣,玩家對人物的控制就可以繞開人物的實時狀態(位置,角度等)直接對人物的模型矩陣產生影響。
萬向節死鎖是尤拉角的一個弊端,這是一個直觀的例子。
四元數
四元數是今天的主角,它能夠很方便的刻畫剛體繞任意軸的旋轉。四元數是一種高階複數,四元數q表示為:
$$q=(x,y,z,w)=xi+yj+zk+w$$
其中,i,j,k滿足:
$$i^2=j^2=k^2=-1$$
$$ij=k,jk=i,ki=j$$
由於i,j,k的性質和笛卡爾座標系三個軸叉乘的性質很像,所以可以將四元數寫成一個向量和一個實陣列合的形式:
$$q=(\vec{v}+w)=((x,y,z),w)$$
可以推匯出四元數的一些運算性質,包括:
* 四元數乘法
$$q1q2=(\vec{v_1}\times \vec{v_2}+w_1\vec{v_2}+w_2\vec{v_1}, w_1w_2-\vec{v_1}\cdot \vec{v_2})$$
* 共軛四元數
$$q^*=(-\vec{v},w)$$
* 四元數的平方模
$$N(q)=N(\vec{v})+w^2$$
* 四元數的逆
$$q^{-1}=\frac{q^*}{N(q)}$$
四元數可以看做是向量和實數的一種更加一般的形式,向量可以視作為實部為0的四元數,而實數可以是作為虛部為0的四元數。上述四元數的運算性質也是實數或向量的運算性質的更一般的形式。
四元數可用來刻畫三維空間中的旋轉,繞單位向量(x,y,z)表示的軸旋轉θ,可令:
$$q=((x,y,z)\sin{\frac{\theta}{2}},\cos{\frac{\theta}{2}})$$
剛體座標系中的點p(P,0)(寫成四元數的形式),旋轉後的座標p'為:
$$p'=qpq^{-1}$$
接下來我們來證明這一點。
首先,我們證明
$qpq^{-1}=(sq)p(sq)^{-1}$
其中s為實數。顯然
$$(sq)p(sq)^{-1}=sqpq^{-1}s^{-1}=sqp^{-1}$$
此時,我們可以將q看做是單位矩陣,因為如果q不是單位矩陣,我們就可以乘以一個常數s將其化為單位矩陣。
然後,我們證明qpq^{-1}和p的模長相等
下面將q視為單位四元數:
$$q^{-1}=q^*$$
四元數q的標量:
$$S(q)=(q+q^*)/2$$
那麼:
$$2S(qpq^{-1})=2S(qpq^*)=qpq^*+(qpq^*)^*=qpq^*+qp^*q^*=q(p+p^*)q^*=q2S(p)q^*=2S(p)$$
最後,我們證明
$$p'=qpq^*$$
如圖所示,u為旋轉軸,旋轉角度為σ,向量v旋轉到w處。旋轉到σ/2處為k(圖中未標出)。
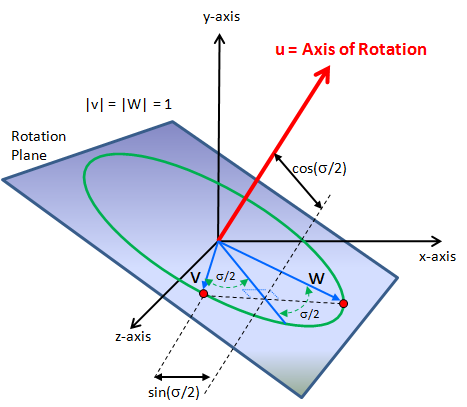
下面也用相同的字母指代四元數,如u就表示向量u的四元數形式((ux,uy,uz),0)。
首先,令u方向上的單位向量為u(為了方便,命名不變,後面的u都是指旋轉軸方向的單位四元數),那麼根據q的定義,參見四元數乘法法則:
$$q=(\vec{u}\sin{\frac{\theta}{2}},\cos{\frac{\theta}{2}})=(\vec{v}\times\vec{k},\vec{v}\cdot \vec{k})=(\vec{v},0)(-\vec{k},0)=kv^*$$
現在令
$$w=qvq^*$$
如果能證明w與v的夾角是σ,那麼就說明w確實是v旋轉σ得到的,整個命題就得證了。
注意v,k和w都是實部為0的單位四元數,表示單位向量,我們有:
$$wk^*=(qvq^{-1})k^*=qvq^*k^*=qvvk^*k^*=q$$
所以
$$wk^*=kv^*$$
上面的式子拆分成實部和虛部,虛部表明w與-k的平面和k與-v的平面重合,實部表明w和-k之間的夾角與k和-v之間的夾角相等,都是π-σ/2。這就說明了w與v的夾角是σ,原命題就得證了。