資料預處理在眾多深度學習演算法中都起著重要作用。實際情況中,將資料做歸一化和白化處理後,很多演算法能夠發揮最佳效果。但是預處理的精確引數並非顯而易見,一般需要嘗試。
1.資料歸一化
資料預處理中標準的第一步是資料歸一化。這一步通常視具體情況選擇。歸一化的一般方法有如下3種:
1.簡單縮放 2.逐樣本均值消減(也稱為移除直流分量) 3.特徵標準化(使資料集中所有特徵都具有零均值和單位方差)
1.1簡單縮放
目的是通過對資料的每一個維度的值進行重新調節(這些維度可能是相互獨立的),使得最終的資料向量落在 [0,1]或[ − 1,1] 的區間內(根據資料情況而定)。這對後續的處理十分重要,因為很多預設引數(如 PCA-白化中的 epsilon)都假定資料已被縮放到合理區間。
例如在處理自然影像時,我們獲得的畫素值在 [0,255] 區間中,常用的處理是將這些畫素值除以 255,使它們縮放到 [0,1] 中。
Matlab函式mapminmax: x為向量。[y,ps]=mapminmax(x)。預設對映範圍為[-1,1]。ps為對映規則,y為對映結果。可以對ps進行設定 ps.ymin和ps.ymax。然後進行自定義範圍對映,當然可以把對本樣本的ps規則應用到其他樣本,如[y,ps]=mapminmax['apply',x1,ps]。實際對映方程y = (ymax-ymin)*(x-xmin)/(xmax-xmin) + ymin。
其他的縮放機制還有atan,log等。具體參考常見的樣本資料歸一化。
1.2逐樣本均值消減
如果資料平穩(即資料每一個維度的統計都服從相同分佈),可以在每個樣本上減去資料的統計平均值。
例子:對於影像,這種歸一化可以移除影像的平均亮度值 (intensity)。很多情況下我們對影像的照度並不感興趣,而更多地關注其內容,這時對每個資料點移除畫素的均值是有意義的。注意:雖然該方法廣泛地應用於影像,但在處理彩色影像時需要格外小心,具體來說,是因為不同色彩通道中的畫素並不都存在平穩特性。
Matlab中對應使用mean()函式求均值。
1.3特徵標準化
特徵標準化指的是(獨立地)使得資料的每一個維度具有零均值和單位方差。這是歸一化中最常見的方法並被廣泛地使用(例如,在使用支援向量機(SVM)時,特徵標準化常被建議用作預處理的一部分)。在實際應用中,特徵標準化的具體做法是:首先計算每一個維度上資料的均值(使用全體資料計算),之後在每一個維度上都減去該均值。下一步便是在資料的每一維度上除以該維度上資料的標準差。
例子:處理音訊資料時,常用 Mel 倒頻係數 MFCCs 來表徵資料。然而MFCC特徵的第一個分量(表示直流分量)數值太大,常常會掩蓋其他分量。這種情況下,為了平衡各個分量的影響,通常對特徵的每個分量獨立地使用標準化處理。、
在Matlab裡面,用於歸一化的方法有premnmx、postmnmx、tramnmx ;prestd、poststd、trastd。其中premnmx指的是歸一到[-1 1],而prestd歸一到單位方差和零均值。
2.PCA和ZCA白化
在做完簡單的歸一化後,白化通常會被用來作為接下來的預處理步驟,它會使我們的演算法工作得更好。實際上許多深度學習演算法都依賴於白化來獲得好的特徵。在進行 PCA/ZCA 白化時,首先使特徵零均值化是很有必要的,這一步需要在計算協方差矩陣前完成。(唯一例外的情況是已經進行了逐樣本均值消減,並且資料在各維度上或畫素上是平穩的。)
接下來在 PCA/ZCA 白化中我們需要選擇合適的 epsilon(回憶一下,這是規則化項,對資料有低通濾波作用)。選取合適的 epsilon 值對特徵學習起著很大作用,下面討論在兩種不同場合下如何選取 epsilon:
2.1基於重構的模型
在基於重構的模型中(包括自編碼器,稀疏編碼,受限 Boltzman 機(RBM),k-均值(K-Means)),經常傾向於選取合適的 epsilon 以使得白化達到低通濾波的效果。(譯註:通常認為資料中的高頻分量是噪聲,低通濾波的作用就是儘可能抑制這些噪聲,同時保留有用的資訊。
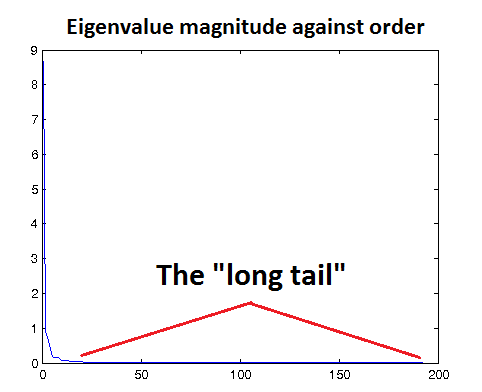
在 PCA 等方法中,假設資料的資訊主要分佈在方差較高的方向,方差較低的方向是噪聲(即高頻分量),因此後文中 epsilon 的選擇與特徵值有關)。一種檢驗epsilon 是否合適的方法是用該值對資料進行 ZCA 白化,然後對白化前後的資料進行視覺化。如果 epsilon 值過低,白化後的資料會顯得噪聲很大;相反,如果 epsilon 值過高,白化後的資料與原始資料相比就過於模糊。一種直觀上得到 epsilon 大小的方法是以圖形方式畫出資料的特徵值,如下圖的例子所示,你可以看到一條"長尾",它對應於資料中的高頻噪聲部分。你需要選取合適的 epsilon,使其能夠在很大程度上過濾掉這條"長尾",也就是說,選取的 epsilon 應大於大多數較小的、反映資料中噪聲的特徵值。
在基於重構的模型中,損失函式有一項是用於懲罰那些與原始輸入資料差異較大的重構結果(譯註:以自動編碼機為例,要求輸入資料經過編碼和解碼之後還能儘可能的還原輸入資料)。如果 epsilon 太小,白化後的資料中就會包含很多噪聲,而模型要擬合這些噪聲,以達到很好的重構結果。因此,對於基於重構的模型來說,對原始資料進行低通濾波就顯得非常重要。
提示:如果資料已被縮放到合理範圍(如[0,1]),可以從epsilon = 0.01或epsilon = 0.1開始調節epsilon。
2.2基於正交化的ICA模型
對基於正交化ICA(獨立主元分析)的模型來說,保證輸入資料儘可能地白化(即協方差矩陣為單位矩陣)非常重要。這是因為:這類模型需要對學習到的特徵做正交化,以解除不同維度之間的相關性(詳細內容請參考 ICA 一節)。因此在這種情況下,epsilon 要足夠小(比如 epsilon = 1e − 6)。
提示:我們也可以在PCA白化過程中同時降低資料的維度。這是一個很好的主意,因為這樣可以大大提升演算法的速度(減少了運算量和引數數目)。確定要保留的主成分數目有一個經驗法則:即所保留的成分的總方差達到總樣本方差的 99% 以上。(詳細內容請參考PCA )
注意: 在使用分類框架時,我們應該只基於練集上的資料計算PCA/ZCA白化矩陣。需要儲存以下兩個引數留待測試集合使用:(a)用於零均值化資料的平均值向量;(b)白化矩陣。測試集需要採用這兩組儲存的引數來進行相同的預處理。
3.具體應用注意事項
❶大影像。採用基於 PCA/ZCA 的白化方法是不切實際的,因為協方差矩陣太大。在這些情況下我們退而使用 1/f 白化方法。
❷自然灰度影像。具有平穩特性,我們通常在第一步對每個資料樣本分別做均值消減(即減去直流分量),然後採用 PCA/ZCA 白化處理,其中的 epsilon 要足夠大以達到低通濾波的效果。
❸彩色影像,色彩通道間並不存在平穩特性。因此我們通常首先對資料進行特徵縮放(使畫素值位於 [0,1] 區間),然後使用足夠大的 epsilon 來做 PCA/ZCA。注意在進行 PCA 變換前需要對特徵進行分量均值歸零化。
❹音訊資料 (MFCC 和頻譜圖),每一維度的取值範圍(方差)不同。例如 MFCC 的第一分量是直流分量,通常其幅度遠大於其他分量,尤其當特徵中包含時域導數 (temporal derivatives) 時(這是音訊處理中的常用方法)更是如此。因此,對這類資料的預處理通常從簡單的資料標準化開始(即使得資料的每一維度均值為零、方差為 1),然後進行 PCA/ZCA 白化(使用合適的 epsilon)。
❺MNIST手寫數字。資料集的畫素值在 [0,255] 區間中。我們首先將其縮放到 [0,1] 區間。實際上,進行逐樣本均值消去也有助於特徵學習。注:也可選擇以對 MNIST 進行 PCA/ZCA 白化,但這在實踐中不常用。
4.中英文對照
歸一化 normalization 白化 whitening 直流分量 DC component 區域性均值消減 local mean subtraction 消減歸一化 sparse autoencoder 縮放 rescaling 逐樣本均值消減 per-example mean subtraction 特徵標準化 feature standardization 平穩 stationary Mel倒頻係數 MFCC 零均值化 zero-mean 低通濾波 low-pass filtering 基於重構的模型 reconstruction based models 自編碼器 autoencoders 稀疏編碼 sparse coding 受限Boltzman機 RBMs k-均值 k-Means 長尾 long tail 損失函式 loss function 正交化 orthogonalization
本文參考:
1.資料預處理 2.資料歸一化彙總
其中,參考2給出了ANN中奇異樣本預處理的程式碼。