蟻群演算法 matlab程式詳細解答-菜鳥也能看懂

sunny落花生發表於2017-05-30
演算法Matlab

後記：沒想到有很多同學會看我寫的這個，因為這是很早前整理的，那時我也剛入門，感覺很潦草，我還是整理一下程式碼，方便大家下載執行，大家可以去我的github下載這個matlab原始檔，main.m

 

最近學習蟻群演算法，單單學習演算法還是不夠深入瞭解，得實際程式設計實現了，理解才能更加透徹，本文根據這篇博文貼出來的程式碼

進行擴充解釋，主要就是做個記錄，其中陰影部分是本人自己加註釋，或許能給剛開始學蟻群演算法和matlab的有一些提示。

 

以下是解放軍資訊工程大學一個老師編的matlab程式，請尊重原作者勞動，引用時請註明出處。

原文地址：http://blog.sina.com.cn/s/blog_5013f7e30100aodx.html

 

 

%設定初始化引數

clear all;
close all;
clc;
C=[1,2;70,90;80,60;10,100;800,200;800,100;90,80;200,600;230,4;500,90];
NC_max=100;
m=18;
Alpha=1;
Beta=5;
Rho=0.5;
Q=1;


%%-------------------------------------------------------------------------
%% 主要符號說明
%% C n個城市的座標，n×2的矩陣
%% NC_max 最大迭代次數
%% m 螞蟻個數
%% Alpha 表徵資訊素重要程度的引數
%% Beta 表徵啟發式因子重要程度的引數
%% Rho 資訊素蒸發係數
%% Q 資訊素增加強度係數
%% R_best 各代最佳路線
%% L_best 各代最佳路線的長度
%%=========================================================================
 

%%第一步：變數初始化
n=size(C,1);%n表示問題的規模（城市個數）
D=zeros(n,n);%D表示完全圖的賦權鄰接矩陣
for i=1:n
    for j=1:n
        if i~=j
            D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
        else
            D(i,j)=eps;      %i=j時不計算，應該為0，但後面的啟發因子要取倒數，用eps（浮點相對精度）表示
        end
        D(j,i)=D(i,j);   %對稱矩陣
    end
end

 

%{

1.C就是城市座標

             x         y

城市1    0     120     


城市2   120     0      
  

城市n   100    230 

 

2.執行後這裡D變成了一個n*n的矩陣，每個元素代表兩個城市之間的距離，比如當城市數目為3時：

D=      城市1    城市2    城市3
 
城市1   0        120      100


城市2  120       0        230 
 
城市3  100    230         0

 

這裡D是個對角線為0的對稱矩陣，因為城市1,2間距離等於城市2,1的距離，城市n與n距離設定為0

 

%}

Eta=1./D;          %Eta為啟發因子，這裡設為距離的倒數
Tau=ones(n,n);     %Tau為資訊素矩陣
Tabu=zeros(m,n);   %儲存並記錄路徑的生成
NC=1;               %迭代計數器，記錄迭代次數
R_best=zeros(NC_max,n);       %各代最佳路線
L_best=inf.*ones(NC_max,1);   %各代最佳路線的長度
L_ave=zeros(NC_max,1);        %各代路線的平均長度
 
while NC<=NC_max        %停止條件之一：達到最大迭代次數，停止
    %%第二步：將m只螞蟻放到n個城市上
        Randpos=[];   %隨機存取
    for i=1:(ceil(m/n))
        Randpos=[Randpos,randperm(n)];
    end
    Tabu(:,1)=(Randpos(1,1:m))';    %此句不太理解？

%{

1.ceil(m/n)

假如有 10只螞蟻，3個城市，ceil(m/n)=ceil（10/3）=4，需要安排四次，才能把這十隻螞蟻全部放到到三個城市，

每次都在行向量Randpos加入如新的元素，randperm(3)表示就是1 3 2，或者3 1 2這種隨機組合，4次迴圈之後，

那麼Randpos =


     2     3     1     1     2     3     3     1     2     3     2     1

 

2.Tabu(:,1)=(Randpos(1,1:m))'

總共m螞蟻，只這裡m為10，Tabu(:,1)表示Tabu第一行就是初始10只螞蟻被隨機分到所三個城市中的一個

Tabu =

     2
     3
     1
     1
     2
     3
     3
     1
     2
     3

這裡只取m=10個數，因為Tabu第一列表示m只螞蟻初始的時候隨機被分在的城市，比如第一個2代表，第一隻螞蟻

最開始放在了城市2，以此類推

 

%}


    %%第三步：m只螞蟻按概率函式選擇下一座城市，完成各自的周遊
    for j=2:n     %所在城市不計算
        for i=1:m    
            visited=Tabu(i,1:(j-1)); %記錄已訪問的城市，避免重複訪問
            J=zeros(1,(n-j+1));       %待訪問的城市
            P=J;                      %待訪問城市的選擇概率分佈
            Jc=1;
            for k=1:n
                if length(find(visited==k))==0   %開始時置0
                J(Jc)=k;
                Jc=Jc+1;                         %訪問的城市個數自加1
                end
            end
            %下面計算待選城市的概率分佈
            for k=1:length(J)
                P(k)=(Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^Beta);
            end
            P=P/(sum(P));
            %按概率原則選取下一個城市
            Pcum=cumsum(P);     %cumsum，元素累加即求和
            Select=find(Pcum>=rand); %若計算的概率大於原來的就選擇這條路線
            to_visit=J(Select(1));
            Tabu(i,j)=to_visit;
        end
    end


 
 

%{

1.visited=Tabu(i,1:(j-1));    向量visited記錄已訪問的城市，比如第一次Tabu中第一行第一個的城市2

2.J=zeros(1,(n-j+1))           向量J記錄待訪問的城市，已結訪問城市2，還沒訪問1和3城市放入J向量中

3.if length(find(visited==k))==0  
判斷語句，find()語句找到visited中等於k的元素在陣列visited中的位置，例如陣列a=[1 2 3 4 5 2],

find(a==2)=[2,6]，find(a==6)=[],則
length(find(a==6))=0
length()==0判斷length()是否為零
如果為零就是visited中沒有k元素，即沒有訪問過k城市。
這時記錄沒有訪問的城市到J中。

%}

 

%下面計算待選城市的概率分佈
for k=1:length(J)

P(k)=(Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^Beta);        

end
P=P/(sum(P));
%按概率原則選取下一個城市
Pcum=cumsum(P);     %cumsum，元素累加即求和
Select=find(Pcum>=rand); %若計算的概率大於原來的就選擇這條路線%要選擇其中總概率大於等於某一個隨機數，找到大於等於這個隨機數的城市的在J中的位置
to_visit=J(Select(1));  %提取這些城市的編號到to_visit中
Tabu(i,j)=to_visit;

%{

1. %visited(end)表示螞蟻現在所在城市編號，J(k)表示下一步要訪問的城市編號

2.P=P/(sum(P));把各個路徑概率統一到和為1

3.Pcum=cumsum(P);   cumsum，元素累加即求和，比如P=[0.1 0.5 0.4]，cumsum(P)=  [0.1000    0.6000    1.0000]

有一點要特別說明，用到cumsum(P)，螞蟻要選擇的下一個城市不是按最大概率，就是要用到輪盤法則，不然影響全域性收縮能力，

所以用到累積函式，Pcum=cumsum(P)

4.Select=find(Pcum>=rand); to_visit=J(Select(1))

輪盤法則，Select(1)，1保證可以選到最大概率的城市，具體自己可以用matlab試一下：

 p=[0.1 0.6 0.3]    中間那個城市概率最大

此時Pcum=[0.1  0.7  1],   Select =[2   3];  Select(1)=2,中間那個城市概率最大
 

%}


 

    if NC>=2
        Tabu(1,:)=R_best(NC-1,:);
    end

 

 

    %%第四步：記錄本次迭代最佳路線
    L=zeros(m,1);     %開始距離為0，m*1的列向量
    for i=1:m
        R=Tabu(i,:);
        for j=1:(n-1)
            L(i)=L(i)+D(R(j),R(j+1));    %原距離加上第j個城市到第j+1個城市的距離
        end
        L(i)=L(i)+D(R(1),R(n));      %一輪下來後走過的距離
    end
    L_best(NC)=min(L);           %最佳距離取最小
    pos=find(L==L_best(NC));
    R_best(NC,:)=Tabu(pos(1),:); %此輪迭代後的最佳路線
    L_ave(NC)=mean(L);           %此輪迭代後的平均距離
    NC=NC+1;                      %迭代繼續

%{

 

 

1.L=zeros(m,1)   記錄本次迭代最佳路線的長度，每個螞蟻都有自己走過的長度記錄在向量L中

%}

    %%第五步：更新資訊素
    Delta_Tau=zeros(n,n);        %開始時資訊素為n*n的0矩陣
    for i=1:m
        for j=1:(n-1)
            Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);          
        %此次迴圈在路徑（i，j）上的資訊素增量
        end
            Delta_Tau(Tabu(i,n),Tabu(i,1))=Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
        %此次迴圈在整個路徑上的資訊素增量
    end
    Tau=(1-Rho).*Tau+Delta_Tau; %考慮資訊素揮發，更新後的資訊素
    %%第六步：禁忌表清零
    Tabu=zeros(m,n);             %%直到最大迭代次數
end

 

%{

1.R_best(NC,:)=Tabu(pos(1),:)：找到路徑最短的那條螞蟻所在的城市先後順序，pos(1)中1表示萬一有長度一樣的兩條螞蟻，那就選第一個

%}


 
%%第五步：更新資訊素
Delta_Tau=zeros(n,n);        %開始時資訊素為n*n的0矩陣
for i=1:m
for j=1:(n-1)
Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);          
%此次迴圈在路徑（i，j）上的資訊素增量
end
Delta_Tau(Tabu(i,n),Tabu(i,1))=Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);    %加上第一個到最後一個城市的資訊素增量
%此次迴圈在整個路徑上的資訊素增量
end
Tau=(1-Rho).*Tau+Delta_Tau; %考慮資訊素揮發，更新後的資訊素
%%第六步：禁忌表清零
Tabu=zeros(m,n);             %%直到最大迭代次數
end

 

 

%{

 

 

1.R_best(NC,:)=Tabu(pos(1),:)：找到路徑最短的那條螞蟻所在的城市先後順序，pos(1)中1表示萬一有長度一樣的兩條螞蟻，那就選第一個

%}

%%第七步：輸出結果
Pos=find(L_best==min(L_best)); %找到最佳路徑（非0為真）
Shortest_Route=R_best(Pos(1),:); %最大迭代次數後最佳路徑
Shortest_Length=L_best(Pos(1)); %最大迭代次數後最短距離
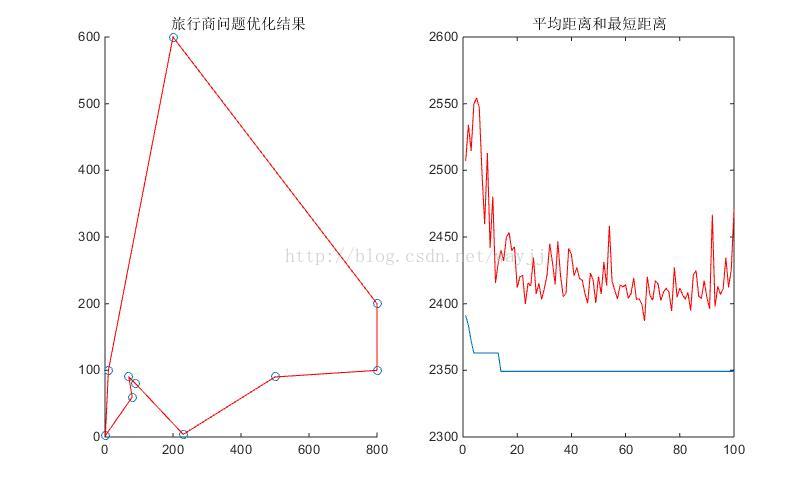
subplot(1,2,1);                  %繪製第一個子圖形
    %%=========================================================================
    %% DrawRoute.m
    %% 畫路線圖的子函式
    %%-------------------------------------------------------------------------
    %% C Coordinate 節點座標，由一個N×2的矩陣儲存
    %% R Route 路線
    %%=========================================================================

    N=length(R);
    scatter(C(:,1),C(:,2));
    hold on
    plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)],'g')
    hold on
    for ii=2:N
        plot([C(R(ii-1),1),C(R(ii),1)],[C(R(ii-1),2),C(R(ii),2)],'g')
        hold on
    end
    title('旅行商問題優化結果 ')

subplot(1,2,2);                  %繪製第二個子圖形

plot(L_best);
hold on ;                        %保持圖形
plot(L_ave,'r');
title('平均距離和最短距離') ;    %標題

 

%{

這部分沒什麼太大問題，多看幾遍就好

%}

 

相關文章