並查集詳解與應用

【導引問題】
題目描述：
某省調查城鎮交通狀況，得到現有城鎮道路統計表，表中列出了每條道路直接連通的城鎮。省政府“暢通工程”的目標是使全省任何兩個城鎮間都可以實現交通（但不一定有直接的道路相連，只要互相間接通過道路可達即可）。問最少還需要建設多少條道路？

輸入：
測試輸入包含若干測試用例。每個測試用例的第1行給出兩個正整數，分別是城鎮數目N ( < 1000 )和道路數目M；隨後的M行對應M條道路，每行給出一對正整數，分別是該條道路直接連通的兩個城鎮的編號。為簡單起見，城鎮從1到N編號。
注意:兩個城市之間可以有多條道路相通,也就是說

3 3
1 2
1 2
2 1

這種輸入也是合法的
當N為0時，輸入結束，該用例不被處理。

輸出：

    對每個測試用例，在1行裡輸出最少還需要建設的道路數目。

樣例輸入：

4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0

樣例輸出：

1
0
2
998

【概念】
英文：Disjoint Set，即“不相交集合”將編號分別為1…N的N個物件劃分為不相交集合，
在每個集合中，選擇其中某個元素代表所在集合。常見兩種操作：
合併兩個集合查詢某元素屬於哪個集合所以，也稱為“並查集”
我們先來看如下的數字集合：集合 A{1,2,3,4}，集合 B{5,6,7}，集合 C{8,0}
我們利用如下樹結構來表示這些集合：

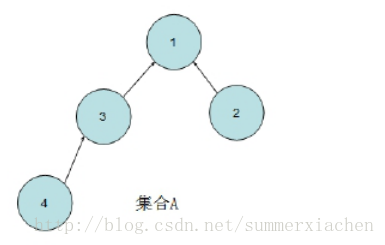
如圖所示，我們用一棵樹上的結點來表示在一個集合中的數字，要判斷兩個數字是否在一個集合中，我們只需判斷它們是否在同一棵樹中。那麼我們使用雙親結點表示法來表示一棵樹，即每個結點儲存其雙親結點。若用陣列來表示如上樹，則得到如下結果：

即我們在陣列單元 i 中儲存結點 i 的雙親結點編號，若該結點已經是根結點則其雙親結點資訊儲存為-1。有了這樣的儲存結構，我們就能通過不斷地求雙親結點來找到該結點所在樹的根結點，若兩個元素所在樹的根結點相同，則可以判定它們在同一棵樹上，它們同屬一個集合。
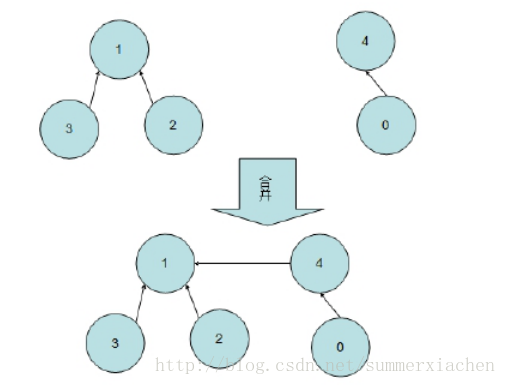
對於合併兩個集合的要求，我們該如何操作呢？我們只需要讓分別代表兩個集合的兩棵樹合併，合併方法為其中一棵樹變為另一棵樹根結點的子樹，如下圖所示：

如圖，若我們對 2 所在的集合與 0 所在的集合合併，則先找到表示 2 所在集合的樹的根結點 1 和表示 0 所在集合的樹的根結點 4，並使其中之一（圖中為 4）為另一個根結點的兒子結點，這樣其中一棵樹變為另一棵樹根結點的一棵新子樹，完成合並。在雙親結點表示法中，該合併過程為：

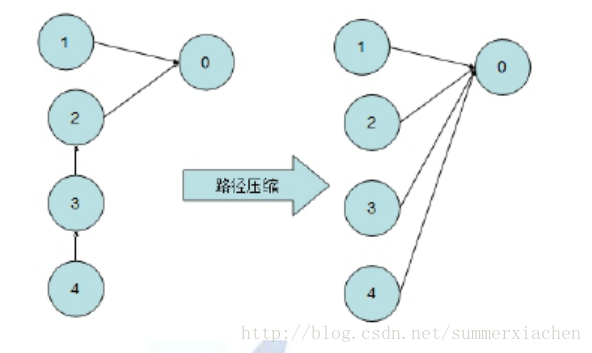
但是，採用這種策略而不加以任何約束也可能造成某些致命的問題。如前文所述，我們對集合的操作主要通過查詢樹的根結點來實現，那麼並查集中最主要的操作即查詢某個結點所在樹的根結點，我們的方法是通過不斷查詢結點的雙親結點直到找到雙親結點不存在的結點為止，該結點即為根結點。那麼，這個過程所需耗費的時間和該結點與樹根的距離有關，即和樹高有關。在我們合併兩樹的過程中，若只簡單的將兩樹合併而不採取任何措施，那麼樹高可能會逐漸增加，查詢根結點的耗時逐漸增大，極端情況下該樹可能會退化成一個單連結串列。為了避免因為樹的退化而產生額外的時間消耗，我們在合併兩棵樹時就不能任由其發展而應該加入一定的約束和優化，使其儘可能的保持較低的樹高。為了達到這一目的，我們可以在查詢某個特定結點的根結點時，同時將其與根結點之間所有的結點都直接指向根結點，這個過程被稱為路徑壓縮，如下圖所示：

【分析】
定義一個陣列，用雙親表示法來表示各棵樹（所有的集合元素個數總和為 N）：int Tree[N];
用 Tree[i]來表示結點 i 的雙親結點，若 Tree[i]為-1 則表示該結點不存在雙親結點，即結點 i 為其所在樹的根結點。
那麼，為了查詢結點 x 所在樹的根結點，我們定義以下函式：

int findRoot(int x) {
if (Tree[x] == -1) return x; //若當前結點為根結點則返回該結點號
else return findRoot(Tree[x]); //否則遞迴查詢其雙親結點的根結點
}

這裡我們將查詢函式寫成了遞迴的形式，不熟悉遞迴的讀者可以參考如下非
遞迴形式的函式：

int findRoot(int x) {
int ret;
while (Tree[x] != -1)
x = Tree[x]; //若當前結點為非根結點則一直查詢其雙親結點
ret = x; //返回根結點編號
return ret;
}

另外若需要在查詢過程中新增路徑壓縮的優化，我們修改以上兩個函式為：

int findRoot(int x) {
if (Tree[x] == -1) return x;
else {
int tmp = findRoot(Tree[x]);
Tree[x] = tmp; //將當前結點的雙親結點設定為查詢返回的根結點編號
return tmp;
}
}

同樣的，其非遞迴形式如下

int findRoot(int x) {
int ret;
int tmp = x;
while (Tree[x] != -1)
x = Tree[x];
ret = x;
x = tmp; //再做一次從結點x到根結點的遍歷
while(Tree[x] != -1) {
int t = Tree[x];
Tree[x] = ret;
x = t; //遍歷過程中將這些結點的雙親結點都設定為已經查詢得到的根結點編號
}
return ret;
}

【問題分析】
題面中描述的是一個實際的問題，但該問題可以被抽象成在一個圖上查詢連通分量（彼此連通的結點集合）的個數，我們只需求得連通分量的個數，就能得到答案（新建一些邊將這些連通分量連通）。
這個問題可以使用並查集完成，初始時，每個結點都是孤立的連通分量，當讀入已經建成的邊後，我們將邊的兩個頂點所在集合合併，表示這兩個集合中的所有結點已經連通。
對所有的邊重複該操作，最後計算所有的結點被儲存在幾個集合中，即存在多少棵樹就能得知共有多少個連通分量（集合）。

#include<iostream>
using namespace std;
#define N 1002
int Tree[N];
int findroot(int x)//找到x節點的根並壓縮路徑。 
{
    int root;
    int temp=x;
    while(Tree[x]!=-1)//找到x節點的根。 
    {
        x=Tree[x];
    }
    root=x;
    x=temp;
    //while(Tree[x]!=-1)與while(x!=root)等同 
    while(x!=root) //路徑壓縮 
    {
        int t=Tree[x];
        Tree[x]=root;
        x=t;
    }
    return root;
}
int main()
{
    int n,m;
    while(cin>>n)
    {
        if(n==0) break;
        cin>>m;
        for(int i=1;i<=n;i++)//初始化。 
            Tree[i]=-1;

        while(m--!=0)
        {
            int a,b;
            cin>>a>>b;
            a=findroot(a);
            b=findroot(b);
            if(a!=b)
            Tree[a]=b;
        }
        int ans=0;
        for(int i=1;i<=n;i++)
        {
            if(Tree[i]==-1) ans++;
        }
        cout<<ans-1<<endl;
    }
 }