一、簡介

並查集，是一種很有用的資料結構。在演算法導論的第22章：用於不相交集合的資料講的就是並查集，看演算法導論確實是需要耐心和耐心的。大致過了一遍，這篇博文將結合自己的理解，舉個生動的例子，並用程式碼實現，讓學習並查集變得有趣。

多個不相交的資料集合可以把它想象為多棵獨立的樹。
並查集的常用基本操作有

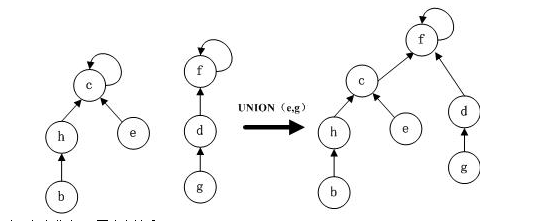
1. 查詢任意兩個樹節點，看看它們是否屬於同一棵樹（其實就是查不同節點的根節點是否一樣即可），如下圖b & e 同屬於根為c的樹，所以它們在同一個集合；而h & g則不屬於同一集合。
2. 合併這些獨立的樹，成為一棵更龐大的樹。（其實也很簡單，就是將一顆樹的根節點成為另一個樹根節點之下的孩子即可）

合併操作如圖所示：

1和2兩步，也就是所謂的查與並。

二、資料結構描述

剛開始我聽這高大上的資料結構名感覺應該會很難，又是樹又是森林什麼的。然而研究了一番發現並查集並不是想象中那麼難，而且特別有意思。

舉個例子，假設有A B兩家公司。 （畫圖是兩棵樹，語言描述如下）
A：
*********6 ——–老闆
******2****3 ——經理
******5****4 ——-員工 （5號員工的直接上司是2號經理，其餘類似）

B：
********8 —– ——老闆
*****1******7 ——經理 （7號經理手下無人）
*****9 —————-部長
*****0 —————員工

並查集的資料結構表示非常簡單直觀，用陣列表示即可。
那麼用一個陣列就可以表示兩家公司的等級構成：
int myboss[ 10 ] = { 9, 8, 6, 6, 3, 2, 6, 8, 8, 1 };
即0號員工的上司是9號，1號員工的上司是8號，2號員工的上司是6號……

這麼簡單的一個陣列就表示了兩棵樹，一個森林，有點意思。

那麼如何實現並 & 查便是並查集的關鍵之處。

三、並查集之並與查

1-查的兩種實現

1）非遞迴方式

查老闆，首先要明確一點就是，老闆的老闆就是自己！開公司就是自己給自己當老闆，多霸氣。
假如我們想查5號員工的老闆是誰？應該怎麼查呢？
思路很簡單，先問5號的上司2號，問問他是不是老闆，他說我不是老闆，我只是普通的經理而已。然後2號經理說，我幫你向上級問問吧。於是2號經理打電話給自己的上司6號，問6號是不是老闆。6號說廢話，我就是你老闆（因為6號沒有上司了）。

通過逐層向上詢問的方式，我們就可以查詢到任意員工的最終老闆是誰。（也就是從任意節點回溯到樹的根節點）

如何用程式碼實現以上的思路呢？
只需以下這個簡單的函式即可：

//不斷向上級詢問找某人的老闆
//老闆的老闆就是自己
int find_boss(int person) {
    int boss = person;  //先假設該員工就是老闆
    int leader,tmp;  //tmp用來儲存某員工的直接上司

    //沒找到老闆則一直迴圈
    while ( myboss[boss] != boss )  
        boss = myboss[boss];

    //*******路徑優化******//
    //每一個人的直接上司都變成老闆（不再是之前的經理或部長了）
    leader = person;  
    while (leader != boss) {
        tmp = myboss[leader];
        myboss[leader] = boss;  //上司直接變成老闆
        leader = tmp;
    }

    return boss;
}

路徑優化

上面的程式碼有一段是所謂的路徑優化。什麼意思呢？
其實很簡單，就是原來的那顆三層的樹，變得只剩下兩層變成
如下形狀：
******6 ——老闆
2***3****4****5 —–經理

也就是說4號和5號員工都升職加薪，走向人生小巔峰了，老闆成為了他們的直接上司（然而，他們手下並沒有員工，光桿司令）。
而什麼時候會發生路徑優化呢？就是每查一次，並查集的層次結構就會改變一點。即，只有打電話問誰是老闆的員工才能獲得機會。
例如執行了 find_boss(5);
那麼公司結構變為：
**********6 ————老闆
******2**5***3 —-經理（5號升職了）
**************4 —-員工（4號仍然是3號的員工，因為他沒有主動打電話給老闆）

假如B公司的9號員工打給老闆要求升職
那麼公司結構則變為：
***********8
********1**7***9
****************0

2）遞迴方式

遞迴方式的查老闆那就更加形象簡單了，路徑優化這一過程多省略了，因為在遞迴回溯的時候就完成了路徑優化，升職加薪了。
程式碼：

//遞迴方式找老闆，在遞迴回溯的過程中同時也實現了路徑優化
//即每個人的直接上司都變成老闆了 r=recursive
int find_boss_r(int person) {
    if( person != myboss[person])
        myboss[person] = find_boss_r(myboss[person]);

    return myboss[person];
}

2.A,B公司合併

並查集另一個重要的操作就是並了。上述例子的A,B兩家公司合併就是並查集的並操作。
那麼如何合併呢？十分簡單形象，加入是A公司收購了B公司，那麼只需要讓B公司的老闆，變為A公司老闆的直接下屬就可以了。

具體實現程式碼：

//合併兩家公司，即A公司老闆成為了B公司老闆的老闆
void join(int person_one, int person_two) {
    int boss_a ,boss_b; 
    boss_a = find_boss(person_one);
    boss_b = find_boss(person_two);

    if (boss_a != boss_b) 
        myboss[boss_b] = boss_a;
}

四、測試程式碼：

int main(int argc,char *argv[])
{
    int boss;

    boss = find_boss(9);
    printf("9號員工的老闆是：%d \n",boss);


    boss = find_boss_r(4);
    printf("4號員工的老闆是：%d \n",boss);

    join(5,0);
    boss = find_boss(7);
    printf("A公司收購B公司後，7號的老闆是： %d\n",boss);

    return 0;
}

五、並查集的應用

理解了並查集可以解決一大類相似的問題，不過具體如何解決還是得看個人功底了。
大家百度一下就有很多難題，在此就省略了。