【演算法】並查集的運用

沐詡發表於2016-08-10
演算法並查集

並查集的概念

並查集顧名思義就是合併和查詢，問題在於合併什麼，查詢什麼。這裡有一種樸素的思想來解釋這兩個問題。就是把這個想成一棵樹。合併什麼？就是把不在這棵樹裡的節點合併到該樹中，而查詢的是該棵樹的根節點。大家可以想象有一棵樹，如下：
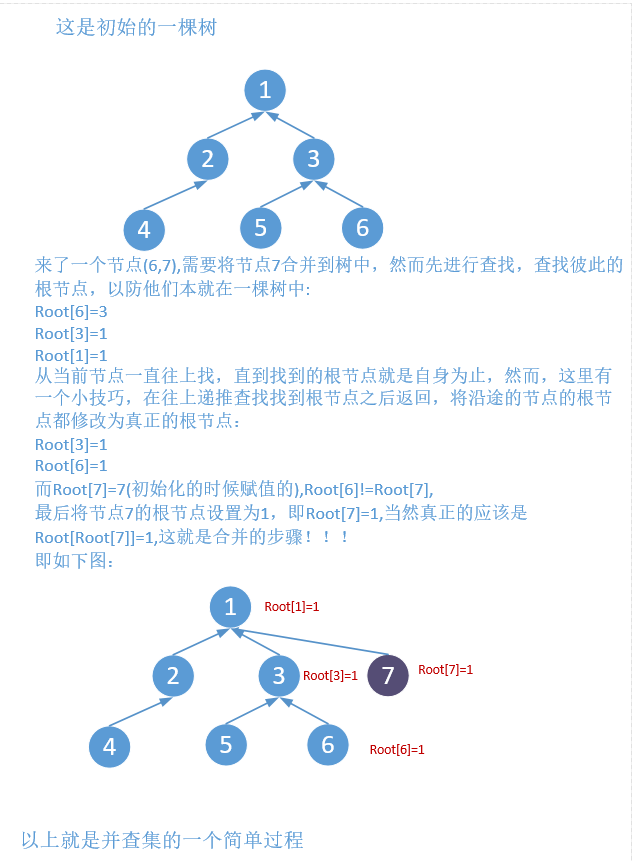
這裡寫圖片描述
從上面可以看出並查集的特點，連通和分類。因此，並查集在演算法中的運用很靈活也很廣泛，比如朋友圈演算法(朋友的朋友是朋友)，團伙問題(朋友的朋友是朋友，敵人的敵人是朋友)，連通圖，最近公共祖先等等。下面將對幾種典型的演算法進行講解。

朋友圈

題目描述：

假如已知有n個人和m對好友關係（存於數字r）。如果兩個人是直接或間接的好友（好友的好友的好友...），則認為他們屬於同一個朋友圈，請寫程式求出這n個人裡一共有多少個朋友圈。

輸入

輸入包含多個測試用例，每個測試用例的第一行包含兩個正整數 n、m，1=<n，m<=100000。接下來有m行，每行分別輸入兩個人的編號f，t（1=<f，t<=n），表示f和t是好友。 當n為0時，輸入結束，該用例不被處理。


對應每個測試用例，輸出在這n個人裡一共有多少個朋友圈。

樣例輸入
5 3
1 2
2 3
4 5
3 3
1 2
1 3
2 3
0
樣例輸出：
2
1
來源：
小米2013年校園招聘筆試題

思路
這題是基本並查集概念的運用。從題中可以看出，關係組只有兩種，一種是朋友，一種是陌生人。說白了，這就是用並查集來分類。同一棵樹中就是同一個朋友圈，分居兩棵樹，就是不同的兩個朋友圈。程式碼如下：

import java.util.Scanner;

public class Main{
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N;
        while((N = sc.nextInt())!=0){
            int M = sc.nextInt();
            int root[] = new int[N+1];
            for(int i=1;i<N+1;i++){//初始化根節點為自己，即各個自為一棵只有一個節點的樹
                root[i]=i;
            }
            while(M-->0){
                int x = sc.nextInt();
                int y = sc.nextInt();
                    union(root,x,y);//合併兩棵樹
            }
            int sum = 0;
            for(int i=1;i<N+1;i++){
                if(root[i]==i){//根節點為自己，表示是當前朋友圈的根節點，如果不是，則表示該節點屬於某個根節點的朋友圈
                    sum++;
                }
            }
            System.out.println(sum);

        }
    }
        //合併的過程
    private static void union(int[] root, int x, int y) {
        int rootx = find(root,x);//遞推尋找根節點
        int rooty = find(root,y);
        if(rootx==rooty){//如果根節點不等，說明兩節點不在同一棵樹中
            return;
        }
        root[rootx]=rooty;//將x節點所在的樹合併到y所在的樹中（注：誰合併誰都無所謂）
    }
       //查詢合併過程
    private static int find(int[] root, int x) {
        if(root[x]!=x){//如果沒找到根節點就繼續往上找，找到根節點之後返回，並沿路修改每個節點的根節點
            root[x]=find(root,root[x]);
        }
        return root[x];
    }
}

團伙問題

題目描述
整個組織有n個人，任何兩個認識的人不是朋友就是敵人，而且滿足：①我朋友的朋友是我的朋友；②我敵人的敵人是我的朋友。所有是朋友的人組成一個團伙。現在，警方委派你協助調查，擁有關於這n個人的m條資訊（即某兩個人是朋友，或某兩個人是敵人），請你計算出這個城市最多可能有多少個團伙。 資料範圍：2≤N≤1000，1≤M≤1000。

輸入資料：
第一行包含一個整數N，第二行包含一個整數M，接下來M行描述M條資訊，內容為以下兩者之一：“x y 1”表示x與y是朋友；“x y 0”表示x與y是敵人（1≤x≤y≤N）。 0為輸入結束。
輸出資料：包含一個整數，即可能的最大團夥數。

樣例輸入：
6 4
1 4 1
3 5 1
4 6 0
1 2 0
0

樣例輸出：
3

思路
該題是上面朋友圈的升級版，唯一不同就是多了一種關係–敵人，所以一共有三種關係：朋友，敵人，陌生人。該題解題的關鍵點在於要能明白：x的敵人y與x之前的敵人是一個朋友圈，y的敵人與x是朋友。假設e[]表示敵人朋友圈，則e[x]與y是同一個朋友圈，或者說e[y]與x是同一個朋友圈，因此便轉換為朋友圈問題。這個一點能明白，解題就很容易了。程式碼如下：

import java.util.Scanner;
public class Main{
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N;
        while((N = sc.nextInt())!=0){
            int M = sc.nextInt();
            int root[] = new int[N+1];
            int e[] = new int[N+1];//存放敵人
            for(int i=1;i<N+1;i++){
                root[i]=i;//根節點為自身
                e[i]=0;//初始化，每個人都沒有敵人
            }
            while(M-->0){
                int x = sc.nextInt();
                int y = sc.nextInt();
                int type = sc.nextInt();
                if(type==1){//如果是朋友，則合併朋友圈
                   union(root,x,y);
                }else{//如果是敵人
                    if(e[x]==0){//如果沒有敵人，則該次關係的敵人就是第一個敵人
                        e[x]=y;
                    }else{
                        union(root,e[x],y);//如果已存在敵人，則去合併敵人朋友圈
                    }
                    if(e[y]==0){//相互記錄
                        e[y]=x;
                    }else{
                        union(root,e[y],x);
                    }
                }
            }
            int sum = 0;
            for(int i=1;i<N+1;i++){
                if(root[i]==i){
                    sum++;
                }
            }
            System.out.println(sum);

        }
    }
    //合併朋友圈(敵人朋友圈)
    private static void union(int[] root, int x, int y) {
        int rootx = find(root,x);
        int rooty = find(root,y);
        if(rootx==rooty){
            return;
        }
        root[rootx]=rooty;
    }
    //查詢根節點
    private static int find(int[] root, int x) {

        if(root[x]!=x){
            root[x]=find(root,root[x]);
        }
        return root[x];
    }
}

連通圖

題目描述：
現在有孤島n個，孤島從1開始標序一直到n，有道路m條（道路是雙向的，如果有多條道路連通島嶼i，j則選擇最短的那條），請你求出能夠讓所有孤島都連通的最小道路總長度。

輸入：
資料有多組輸入。
每組第一行輸入n(1<=n<=1000),m(0<=m<=10000)。

輸出：
對每組輸入輸出一行，如果能連通，輸出能連通所有島嶼的最小道路長度，否則請輸出字串”no”。

樣例輸入：
3 5
1 2 2
1 2 1
2 3 5
1 3 3
3 1 2
4 2
1 2 3

樣例輸出：
3
no
這題除了考並查集，其實也是對kruskal演算法的運用。如果大家知道kruskal，就知道首先應該是按距離排序，然後每次選擇最短路徑連線，一點點成為樹的合併，最後合成為一棵最小生成樹。程式碼如下：


import java.util.Comparator;
import java.util.Scanner;
//儲存邊的結構，u->v距離為len
class Edg{
    int u;
    int v;
    int len;
}
public class Main{
    public static void main(String[] args) {
        Scanner sc =  new Scanner(System.in);
        while(sc.hasNext()){
            int N =  sc.nextInt();
            int M = sc.nextInt();
            int root[] = new int[N+1];
            for(int i=1;i<N+1;i++){
                root[i]=i;
            }
            Edg[] edg = new Edg[M];
            //邊的輸入
             for(int i=0;i<M;i++){
                edg[i] = new Edg();
                edg[i].u = sc.nextInt();
                edg[i].v = sc.nextInt();
                edg[i].len = sc.nextInt();  
             }
             //將邊按路徑排序
             java.util.Arrays.sort(edg, new Comparator<Edg>() {

                @Override
                public int compare(Edg a, Edg b) {
                    if(a.len>b.len){
                        return 1;
                    }else if(a.len<b.len){
                        return -1;
                    }else{
                        return 0;
                    }
                }
            });

             int sum=0;
             int eds = 0;//合併的生成樹中的邊樹
             for(int i=0;i<M;i++){
             //檢視u/v根節點是否相等，如果相等表示他們已經連通。
                 int rootu = find(root,edg[i].u);
                 int rootv = find(root,edg[i].v);
                 if(rootu!=rootv){//不連通，則合併兩棵樹，其實也就是將u節點所在的樹合併到v中
                     root[rootu]=rootv;                             
                     eds++;
                     sum+=edg[i].len;//最小生成樹中的連通距離
                 }
                 //如果合成的生成樹邊樹等於節點總數N-1，則已經是最小生成樹。
                 if(eds==N-1){
                     break;
                 }
             }
             if(eds==N-1){
               System.out.println(sum);
             }else{
                 System.out.println("no");
             }
        }
    }

    private static int find(int[] root, int x) {
        return root[x]==x?x:(root[x]=find(root,root[x]));
    }
}

總結

以上是並查集中比較重要的演算法，對於最近公共祖先的問題，在我之前有專門有幾篇部落格講解了，大家如果有必要可以在我的部落格目錄中查詢。上面的題目在九度oj中可以找到，但是JAVA無法AC，我改成C++可以AC。講的不是特別明白，也可能有誤，歡迎大家拍磚！！！

相關文章