並查集的初級應用及進階
並查集的初級應用及進階
一、精華
精華提煉1:
內容:並查集就是樹的孩子表示法的應用。
解釋:對於下圖所示樹,它的孩子表示法為:
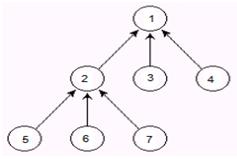
belg[5]=2, belg[6]=2, belg[7]=2;
belg[2]=1, belg[3]=1, belg[4]=1;
belg[1]=1(也可以=-1,只要能夠識別它是根就可以)
精華提煉2:
內容:並查集的孩子父親表示法中,每個節點與其父親節點可以新增一個關係屬性(必須具有可傳遞性)。
解釋:比如,節點表示一個人,關係屬性為一個人的性別。我們先用上圖來解釋這個關係屬性的應用,在後文具體展開。我們可以這樣定義,如果節點i和其父節點j性別相同(belg[i]=j),則kind[i]=false, 反之,kind[i]=true,那麼如果我們知道kind[5]=true,kind[2]=false,那麼5和2的父節點1的關係為kind[5]^kind[2]=true,即他們性別不同。
二、基礎
基礎1:集合表示
根據精華提煉1,我們把一顆樹的節點集合看成以根節點命名的集合,那麼上面的集合我們可以認為是集合1。
下圖共有兩個集合,分別為集合1,集合2。
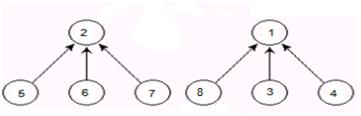
基礎2:元素關係
如何判斷元素關係呢?其實,我們只需找出元素對應的集合名稱,然後判斷名稱是否相同即可。尋找集合名稱程式碼如下:
int Find(int x)
{
while ( belg[x]!=x )
{
x = belg[x];
}
return x;
}
例如:對於基礎1中左圖,有belg[5]=2,belg[2]=2。那麼5屬於集合2。
現在我們已經解決了元素關係問題。
基礎3:集合合併
集合如何合併呢?基礎2中,我們已經可以找到元素對應集合的名稱(即根節點標號),如果元素u、v(u、v不在同一集合)對應的集合名稱為_u、_v,那麼語句belg[_u]=_v什麼意思呢?想到了吧?就是把集合_u與集合_v合併,並且以_v命名。
至此,通過基礎部分我們知道了什麼是並查集,通過精華提煉部分,我們知道了並查集的高階應用(精華提煉2)。
三、優化
雖然我們已經知道了基礎的並查集,但是大家有沒有想過簡單用上面介紹的集合合併可能造成集合(樹)的退化。比如對只有一個元素的集合1到集合n進行下述操作:把集合1合併到集合2,把集合2合併到集合3,…… 把集合n-1合併到集合n,那麼生成一個含有n各元素的集合n,它的結構如下:

那麼,每次判斷n所屬集合都要n次操作,即複雜度為O(n),這個耗費是不是必須的呢?其實不然。
優化1:路徑壓縮
對於上圖退化的集合,它的表示是這樣的:belg[n]=n-1, belg[n-1]=n-2, …… belg[2]=1, belg[1]=1;
既然上面元素都屬於集合1,那麼我們是不是可以這樣做呢?belg[n]=1,belg[n-1]=1,……belg[2]=1,belg[1]=1;即把查詢n所屬集合時形成的路徑上的點直接連到根節點上。可以的,因為這樣操作只改變集合樹的結構,並沒有改變這個集合的元素。
關於路徑壓縮,可以在查詢過程中實現,那麼對於上述退化樹,查詢n第一次要n次操作,以後就只需一次操作。實現如下:
版本一:(遞迴)
int Find(int x)
{
return x==belg[x]?x:(belg[x]=Find(belg[x]));
}
程式碼很短,遞迴次數多時,不建議使用。
版本二:(迭代)
int Find(int x)
{
int _b, _x = x;
while ( belg[_x]!=_x )
{
_x = belg[_x];
}
while ( belg[x]!=x )
{
_b = belg[x];
belg[x] = _x;
x = _b;
}
return _x;
}
程式碼長點,但是少了遞迴過程,效率高點。
優化2:優化合並
合理的安排合併方式,可以防止退化,例如對於上述退化的例子,我們把元素少的集合合併到元素多的集合上。即集合2合併到集合1,集合3合併到集合1,……集合n合併到集合1,那麼產生的樹結構為:
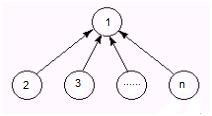
不過這個優化代價也很大的,因為要對開一個整型陣列來記錄集合元素個數,然後,再集合i和集合j合併時,通過判斷集合中元素個數來實現合併:
int Union(int i, int j)
{
if ( sum[i]>sum[j] )
{
belg[j] = i;
}
else
{
belg[i] = j;
}
}
細心的讀者,可能想到這個優化並不能完全避免集合退化,是的,所以我認為不必開闢陣列浪費空間進行這個優化,完全可以隨機法來由優化,比如:
int Union(int i, int j)
{
if ( rand()&1 )
{
belg[j] = i;
}
else
{
belg[i] = j;
}
}
通過隨機值的奇偶性來決定怎麼合併,平均效果是很好的。
上面詳細講了這麼多理論性的東西,下面開始介紹應用:
四、應用
基礎應用:
題目:
有n個人(1..n),如果i和j是親戚,j和k是親戚,那麼j和k也是親戚,題目給定n各人的m對親戚關係,然後提出q各問題,問你某兩個人是不是親戚。
解答:
並查集簡單應用,程式碼如下:
#include <iostream>
using namespace std;
const int MAXN = 1010;
int belg[MAXN];
int main()
{
int i, u, v, n, m, q;
scanf("%d", &n);
for ( i=1; i<=n; belg[i]=i,++i );
scanf("%d", &m);
for ( i=1; i<=m; ++i )
{
scanf("%d%d", &u, &v);
u = Find(u); v = Find(v);
if ( u!=v ) { Union(u,v); }
}
scanf("%d", &q);
for ( i=1; i<=q; ++i )
{
scanf("%d%d", &u, &v);
u = Find(u); v = Find(v);
printf("%s/n", (u==v?"YES":"NO"));
}
return 0;
}
其中Find函式和Union函式參見上面的介紹。
高階應用:
題目:(HDU1829)
有n各小動物,它們只有異性之間才配對,同性之間不會配對。給定m對配對關係,問你是否能通過分配性別給n各小動物,使這m各配對關係成立,即不會出現同性之間配對。
解答:
這裡我們使用在精華提煉二中提到的思路。
首先,我們必須明確兩點:1.這裡的屬於同一個集合的元素表示他們的關係已經確定,比如元素i和元素j屬於同一個集合,那麼他們要麼同性,要麼異性,關係時確定的。2.同一個集合的樹表示中,節點i和它的父親節點j關係儲存在kind[i]中。
同時,我們約定,如果節點i和節點j性別相同,則關係為false,否則關係為true。根節點root滿足kind[root]=false,因為自己跟自己性別肯定相同(當然不包括人妖了哈^-^)。
關係的運算我們可以通過異或(提示1)來實現,如果i和j關係為r1,i和k關係為r2,那麼j和k關係為r1^r2。
上面的分析已經足夠我們處理這個題目了。下面給出程式碼:
#include <iostream>
using namespace std;
const int MAXN = 2010;
int belg[MAXN];
bool kind[MAXN];
int Find(int x, bool &s);
int main()
{
int i, k, n, m;
int u, v, _u, _v, cas;
bool flag, su, sv;
scanf("%d", &cas);
for ( k=1; k<=cas; ++k )
{
scanf("%d%d", &n, &m);
for ( i=1; i<=n; ++i )
{
belg[i] = i;
kind[i] = false;
}
for ( i=1,flag=true; i<=m; ++i )
{
scanf("%d%d", &u, &v);
if ( flag )
{
_u = Find(u,su=false);
_v = Find(v,sv=false);
if ( _u==_v )
{
flag = su^sv;
}
else
{
belg[_u] = _v;
kind[_u] = !(su^sv);
}
}
}
printf("Scenario #%d:/n", k);
if ( flag )
{
printf("No suspicious bugs found!/n/n");
}
else
{
printf("Suspicious bugs found!/n/n");
}
}
return 0;
}
int Find(int x, bool &s)
{
int h;
if ( belg[x]==x )
{
h = x; s = false;
}
else
{
h = Find(belg[x],s);
belg[x] = h;
s = kind[x]^s;
kind[x] = s;
}
return h;
}
由於上述Find函式使用了遞迴所以比較耗時(1609毫秒,132KB),可以改為如下的迭代形式(671毫秒,0KB):
int Find(int x, bool &s)
{
int _x, h = x;
bool s1, s2;
while ( belg[h]!=h )
{
s = s^kind[h];
h = belg[h];
}
s1 = s;
while ( belg[x]!=x )
{
_x = belg[x];
belg[x] = h;
s2 = kind[x];
kind[x] = s1;
s1 = s1^s2;
x = _x;
}
return h;
}
提示1.異或:i和j異或就是:如果i和j相同則為false,否則為true,比如i=true,j=false,則i異或j為true。i=false,j=false,則i異或j為false。
相關文章
- 並查集的分析及應用並查集
- 並查集の進階用法並查集
- 並查集的應用並查集
- 並查集應用並查集
- 並查集—應用並查集
- 並查集的應用2並查集
- 並查集深度應用並查集
- 並查集以及應用並查集
- 並查集的簡單應用並查集
- 並查集(二)並查集的演算法應用案例上並查集演算法
- 並查集應用總結並查集
- 並查集的應用:hdu 1213並查集
- 社交網路 (並查集的應用)並查集
- WinRAR初級中級高階等應用
- 並查集詳解與應用並查集
- 並查集擴充套件應用並查集套件
- 食物鏈(並查集的簡單應用)並查集
- Java初級~中級~高階進階之路Java
- 並查集經典應用場景並查集
- 【學習筆記】並查集應用筆記並查集
- 並查集(Union-Find) 應用舉例並查集
- 【帶權並查集】理論和應用並查集
- 並查集 (Union-Find Sets)及其應用並查集
- 並查集在實際問題中的應用並查集
- 資料結構 — 並查集的原理與應用資料結構並查集
- 【並查集】【帶偏移的並查集】食物鏈並查集
- 並查集到帶權並查集並查集
- 並查集(一)並查集的幾種實現並查集
- 【演算法】並查集的運用演算法並查集
- 並查集(Union-Find) 應用舉例 --- 基礎篇並查集
- 資料結構之Kruskal演算法(並查集的應用)資料結構演算法並查集
- 並查集的使用並查集
- 並查集演算法Union-Find的思想、實現以及應用並查集演算法
- 初學進階
- 初級進階版SQL語句總結(1)SQL
- 3.1並查集並查集
- 並查集(小白)並查集
- VI高階命令集錦及VIM應用例項(轉)