Node.js軟肋之回撥大坑

Node.js需要按順序執行非同步邏輯時一般採用後續傳遞風格，也就是將後續邏輯封裝在回撥函式中作為起始函式的引數，逐層巢狀。這種風格雖然可以提高CPU利用率，降低等待時間，但當後續邏輯步驟較多時會影響程式碼的可讀性，結果程式碼的修改維護變得很困難。根據這種程式碼的樣子，一般稱其為\"callback hell\"或\"pyramid of doom\"，本文稱之為回撥大坑，巢狀越多，大坑越深。

坑的起源

後續傳遞風格

為什麼會有坑？這要從後續傳遞風格（continuation-passing style--CPS)說起。這種程式設計風格最開始是由Gerald Jay Sussman和Guy L. Steele, Jr. 在AI Memo 349上提出來的，那一年是1975年，Schema語言的第一次亮相。既然JavaScript的函數語言程式設計設計原則主要源自Schema，這種風格自然也被帶到了Javascript中。

這種風格的函式要有額外的引數：“後續邏輯體”，比如帶一個引數的函式。CPS函式計算出結果值後並不是直接返回，而是呼叫那個後續邏輯函式，並把這個結果作為它的引數。從而實現計算結果在邏輯步驟之間的傳遞，以及邏輯的延續。也就是說如果要呼叫CPS函式，呼叫方函式要提供一個後續邏輯函式來接收CPS函式的“返回”值。

回撥

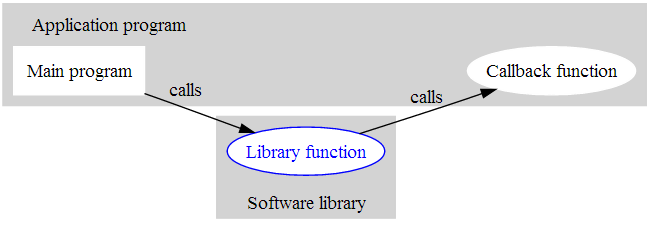
在JavaScript中，這個“後續邏輯體”就是我們常說的回撥(callback)。這種作為引數的函式之所以被稱為回撥，是因為它一般在主程式中定義，由主程式交給庫函式，並由它在需要時回來呼叫。而將回撥函式作為引數的，一般是一個會佔用較長時間的非同步函式，要交給另一個執行緒執行，以便不影響主程式的後續操作。如下圖所示：

在JavaScript程式碼中，後續傳遞風格就是在CPS函式的邏輯末端呼叫傳入的回撥函式，並把計算結果傳給它。但在不需要執行處理時間較長的非同步函式時，一般並不需要用這種風格。我們先來看個簡單的例子，程式設計求解一個簡單的5元方程：

\x+y+z+u+v=16\x+y+z+u-v=10\x+y+z-u=11\x+y-z=8\x-y=2\

對於x+y=a;x-y=b這種簡單的二元方程我們都知道如何求解，這個5元方程的運算規律和這種二元方程也沒什麼區別，都是兩式相加除以2求出前一部分，兩式相減除以2求出後一部分。5元方程的前一部分就是4元方程的和值，依次類推。我們的程式寫出來就是：

\

程式碼清單1. 普通解法-calnorm.js

\

\var res = new Int16Array([16,10,11,8,2]),l= res.length;\var variables = [];\for(var i = 0;i \u0026lt; l;i++) {\    if(i === l-1) {\        variables[i] = res[i];\    }else {\      variables[i] = calculateTail(res[i],res[i+1]);\      res[i+1] = calculateHead(res[i],res[i+1]);\    }\}\function calculateTail(x,y) {\    return (x-y)/2;\}\function calculateHead(x,y) {\    return (x+y)/2;\}\

方程式的結果放在了一個整型陣列中，我們在迴圈中依次遍歷陣列中的頭兩個值res[i]和res[i+1]，用calculateTail計算最後一個單值，比如第一和第二個等式中的v；用calculateHead計算等式的\"前半部分\"，比如第一和第二個等式中的x+y+z+u部分。並用該結果覆蓋原來的差值等式，即用x+y+z+u的結果覆蓋原來x+y+z+u-v的結果，以便計算下一個tail，直到最終求出所有未知數。

如果calculateTail和calculateHead是CPU密集型的計算，我們通常會把它放到子執行緒中執行，並在計算完成後用回撥函式把結果傳回來，以免阻塞主程式。關於CPU密集型計算的相關概念，可參考本系列的上一篇Node.js軟肋之CPU密集型任務。比如我們可以把程式碼改成下面這樣：

\

程式碼清單2. 回撥解法-calcb.js

\

\var res = new Int16Array([16,10,11,8,2]),l= res.length;\var variables = [];\(function calculate(i) {\    if(i === l-1) {\        variables[i] = res[i];\        console.log(i + \":\" + variables[i]); \        process.exit();\    }else {\        calculateTail(res[i],res[i+1],function(tail) {\            variables[i] = tail;\            calculateHead(res[i],res[i+1],function(head) {\                res[i+1] = head;\                console.log('-----------------'+i+'-----------------')\                calculate(i+1);\            });\        });\    }\})(0);\function calculateTail(x,y,cb) {\   setTimeout(function(){\        var tail = (x-y)/2;\        cb(tail);\    },300);\}\function calculateHead(x,y,cb) {\    setTimeout(function(){\        var head = (x+y)/2;\        cb(head);\    },400);\}\

\

跟上一段程式碼相比，這段程式碼主要有兩個變化。第一是calculateTail和calculateHead裡增加了setTimeout，把它們偽裝成CPU密集型任務；第二是棄用for迴圈，改用函式遞迴。因為calculateHead的計算結果會影響下一輪的calculateTail計算，所以calculateHead計算要阻塞後續計算。而for迴圈是無法阻塞的，會產生錯誤的結果。此外就是calculateTail和calculateHead都變成後續傳遞風格的函式了，通過回撥返回最終計算結果。

這個例子比較簡單，既不能充分體現回撥在處理非同步非阻塞操作時在效能上的優越性，坑的深度也不夠恐怖。不過也可以說明“用後續傳遞風格實現幾個非同步函式的順序執行是產生回撥大坑的根本原因”。下面有一個更抽象的回撥樣例，看起來更有代表性：

\module.exports = function (param, cb) {\  asyncFun1(param, function (er, data) {\    if (er) return cb(er);\    asyncFun2(data,function (er,data) {\      if (er) return cb(er);\      asyncFun3(data, function (er, data) {\        if (er) return cb(er);\        cb(data);\      })\    })\  })\}\

像function(er,data)這種回撥函式簽名很常見，幾乎所有的Node.js核心庫及第三方庫中的CPS函式都接收這樣的函式引數，它的第一個引數是錯誤，其餘引數是CPS函式要傳遞的結果。比如Node.js中負責檔案處理的fs模組，我們再看一個實際工作中可能會遇到的例子。要找出一個目錄中最大的檔案，處理步驟應該是：

1. 用fs.readdir獲取目錄中的檔案列表；\
2. 迴圈遍歷檔案，獲取檔案的stat；\
3. 找出最大檔案；\
4. 以最大檔案的檔名為引數呼叫回撥。\

這些都是非同步操作，但需要順序執行，後續傳遞風格的程式碼應該是下面這樣的：

\

程式碼清單3. 尋找給定目錄中最大的檔案

\

\var fs = require('fs')\var path = require('path')\module.exports = function (dir, cb) {\  fs.readdir(dir, function (er, files) { // [1]\    if (er) return cb(er)\    var counter = files.length\    var errored = false\    var stats = []\    files.forEach(function (file, index) {\      fs.stat(path.join(dir,file), function (er, stat) { // [2]\        if (errored) return\        if (er) {\          errored = true\          return cb(er)\        }\        stats[index] = stat // [3]\        if (--counter == 0) { // [4]\          var largest = stats\            .filter(function (stat) { return stat.isFile() }) // [5]\            .reduce(function (prev, next) { // [6]\              if (prev.size \u0026gt; next.size) return prev\              return next\            })\          cb(null, files[stats.indexOf(largest)]) // [7]\        }\      })\    })\  })\}\

\

對這個模組的使用者來說，只需要提供一個回撥函式function(er,filename)，用兩個引數分別接收錯誤或檔名：

\var findLargest = require('./findLargest')\findLargest('./path/to/dir', function (er, filename) {\  if (er) return console.error(er)\  console.log('largest file was:', filename)\})\

介紹完CPS和回撥，我們接下來看看如何平坑。

解套平坑

編寫正確的併發程式歸根結底是要讓儘可能多的操作同步進行，但各操作的先後順序仍能正確無誤。服務端的程式碼一般邏輯比較複雜，步驟多，此時用巢狀實現非同步函式的順序執行會比較痛苦，所以應該儘量避免巢狀，或者降低巢狀程式碼的複雜性，少用匿名函式。這一般有幾種途徑：

1. 最簡單的是把匿名函式拿出來定義成單獨的函式，然後或者像原來一樣用巢狀方式呼叫，或者藉助流程控制模組放在陣列裡逐一呼叫；\
2. 用Promis；\
3. 如果你的Node版本\u0026gt;=0.11.2，可以用generator。\

我們先介紹最容易理解的流程控制模組。

流程控制模組

Nimble是一個輕量、可移植的函式式流程控制模組。經過最小化和壓縮後只有837位元組，可以執行在Node.js中，也可以用在各種瀏覽器中。它整合了underscore和async一些最實用的功能，並且API更簡單。

nimble有兩個流程控制函式，_.parallel和_.series。顧名思義，我們要用的是第二個，可以讓一組函式序列執行的_.series。下面這個命令是用來安裝Nimble的：

\npm install nimble\

如果用.series排程執行上面那個解方程的函式，程式碼應該是這樣的：

\...\var flow = require('nimble');\(function calculate(i) {\    if(i === l-1) {\        variables[i] = res[i];\        process.exit();\    }else {\        flow.series([\            function (callback) {\                calculateTail(res[i],res[i+1],function(tail) {\                    variables[i] = tail;\                    callback();\                });\            },\            function (callback) {\                calculateHead(res[i],res[i+1],function(head) {\                    res[i+1] = head;\                    callback();\                });\            },\            function(callback){\                calculate(i+1);\            }]);\    }\})(0);\...\

.series陣列引數中的函式會挨個執行，只是我們的calculateTail和calculateHead都被包在了另一個函式中。儘管這個用流程控制實現的版本程式碼更多，但通常可讀性和可維護性要強一些。接下來我們介紹Promise。

Promise

什麼是Promise呢？在紙牌屋的第一季第一集中，當琳達告訴安德伍德不能讓他做國務卿後，他說：“所謂Promise，就是說它不會受不斷變化的情況影響。”

Promise不僅去掉了巢狀，它連回撥都去掉了。因為按照Promise的觀點，回撥一點也不符合函數語言程式設計的精神。回撥函式什麼都不返回，沒有返回值的函式，執行它僅僅是因為它的副作用。所以用回撥函式程式設計天生就是指令式的，是以副作用為主的過程的執行順序，而不是像函式那樣把輸入對映到輸出，可以組裝到一起。

最好的函數語言程式設計是宣告式的。在指令式程式設計中，我們編寫指令序列來告訴機器如何做我們想做的事情。在函數語言程式設計中，我們描述值之間的關係，告訴機器我們想計算什麼，然後由機器（底層框架）自己產生指令序列完成計算。Promise把函式的結果變成了一個與時間無關的值，就像算式中的未知數一樣，可以用它輕鬆描述值之間的邏輯計算關係。雖然要得出一個函式最終的結果需要先計算出其中的所有未知數，但我們寫的程式只需要描述出各未知數以及未知數和已知數之間的邏輯關係。而CPS是手工編排控制流，不是通過定義值之間的關係來解決問題，因此用回撥函式編寫正確的併發程式很困難。比如在程式碼清單2中，caculateHead被放在caculateTail的回撥中執行，但實際上在計算同一組值時，兩者之間並沒有依賴關係，只是進入下一輪計算前需要兩者都給出結果，但如果不用回撥巢狀，實現這種順序控制比較麻煩。

\

當然，這和我們的處理方式（共用陣列）有關，就這個問題本身而言，caculateHead完全不依賴於任何caculateTail。

\

這裡用的Promis框架是著名的Q，可以用npm install q安裝。雖然可用的Promis框架有很多，但在它們用法上都大同小異。我們在這裡會用到其中的三個方法。

第一個負責將Node.js的CPS函式變成Promise。Node.js核心庫和第三方庫中有非常多的CPS函式，我們的程式肯定要用到這些函式，要解決回撥大坑，就要從這些函式開始。這些函式的回撥函式引數大多遵循一個相同的模式，即函式簽名為function(err, result)。對於這種函式，可以用簡單直接的Q.nfcall和Q.nfapply呼叫這種Node.js風格的函式返回一個Promise：

\return Q.nfcall(FS.readFile, \"foo.txt\