Codeforces 478D Red-Green Towers：dp

Leohh發表於2018-01-10

題目連結：http://codeforces.com/problemset/problem/478/D

題意：

　　給你r個紅方塊和g個綠方塊，讓你用這些方塊堆一個塔。

　　最高層有1個方塊，每往下一層塊數+1，同時要保證每層中的方塊都是同一種顏色。

　　如圖：

　　

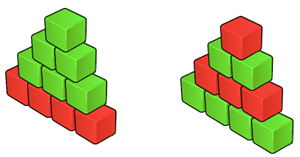
　　問你在塔的高度最高的前提下，堆出塔的方案數。

 

題解：

　　假設塔最高能堆d層，則：

　　　　d*(d+1)/2 <= r+g

　　解得：

　　　　d = floor((-1+sqrt(1+8*(r+g)))/2)

　　　　並且d最大不超過900。

　　表示狀態：

　　　　dp[i][j] = numbers

　　　　表示已經堆了最上面的i層，用了j個紅方塊，此時的方法數。

　　

　　找出答案：

　　　　ans = ∑ dp[d][max(0,d*(d+1)/2-g) to r]

　　　　因為最終還要保證用了綠方塊的個數 <= g，所以列舉i至少要從d*(d+1)/2-g開始。

 

　　如何轉移：

　　　　dp[i][j] = dp[i-1][j] + dp[i-1][j-i]

　　　　從上往下數第i層可能全用綠色，或全用紅色

 

　　邊界條件：

　　　　dp[0][0] = 1

 

　　另外要用滾動陣列，否則會MLE。

 

AC Code:

 1 #include <iostream>
 2 #include <stdio.h>
 3 #include <string.h>
 4 #include <math.h>
 5 #define MAX_D 900
 6 #define MAX_R 200005
 7 #define MOD 1000000007
 8 #define EPS 1e-5
 9 
10 using namespace std;
11 
12 int r,g,d;
13 int dp[2][MAX_R];
14 
15 int main()
16 {
17     cin>>r>>g;
18     d=floor((-1.0+sqrt(1.0+8.0*(r+g))+EPS)/2.0);
19     memset(dp,0,sizeof(dp));
20     dp[0][0]=1;
21     for(int i=1;i<=d;i++)
22     {
23         for(int j=0;j<=r;j++)
24         {
25             dp[i&1][j]=dp[(i-1)&1][j];
26             if(j-i>=0) dp[i&1][j]+=dp[(i-1)&1][j-i];
27             dp[i&1][j]%=MOD;
28         }
29     }
30     int ans=0;
31     for(int i=max(0,d*(d+1)/2-g);i<=r;i++)
32     {
33         ans=(ans+dp[d&1][i])%MOD;
34     }
35     cout<<ans<<endl;
36 }

 

相關文章